Александр Кушнеров
10.01.2025

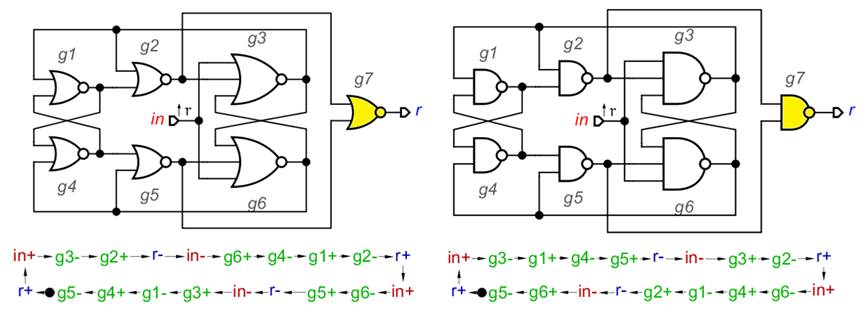
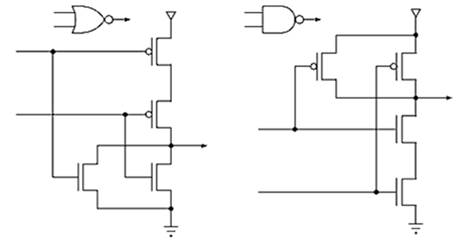
 Аннотация – Дизайн замкнутых комбинационных схем основан на законах поглощения конъюнкций и дизъюнкций. Если в такой схеме используется только один выход, то её транзисторная реализация будет избыточной, а граф этой реализации будет содержать ложные циклы. Значения на выходах комбинационной схемы, в том числе и замкнутой, можно считать правильными лишь через какое-то время, необходимое для завершения всех переходных процессов. В статье показано как дополнить замкнутую схему индикатором завершения переходных процессов, т.е. сделать её асинхронной.

1. Введение

Замыкание выхода комбинационной схемы на один или несколько её входов может дать новую комбинационную схему. Поскольку данные обрабатываются от входов к выходам, обратную связь можно представить как направленную петлю на графе. С другой стороны, графы, которые задают контактные мостиковые схемы, содержат не направленные петли (циклы). Именно из-за петель такие схемы часто являются минимальными. Преобразование графа мостиковой схемы в последовательно-параллельный соответствует схеме на логических элементах. Это преобразование размыкает все петли и называется декомпозиция в базисе И/ИЛИ. Мы будем рассматривать декомпозицию, которая даёт минимальное количество логических элементов. Чтобы корректно замкнуть полученные схемы нужно выполнить определённые условия. В качестве этих условий мы используем известную замкнутую схему.

В инженерной практике релейно-контактные мостиковые схемы начали использоваться по крайней мере со второй половины 1890-х годов [1]. Однако, привлечение булевой алгебры для их анализа и синтеза состоялось лишь во второй половине 1930-х годов [2]. Рассмотрим простейшую мостиковую схему из пяти замыкающих ключей (контактов), назовём её K5. Каждый ключ в этой схеме управляется своей переменной. Присвоить переменные можно например так, как показано в Табл. 1. Последовательное соединение ключей записывается как произведение переменных, а параллельное – как сумма. Таким образом, чтобы записать булеву функцию схемы в дизъюнктивной нормальной форме (ДНФ), нужно найти все возможные пути от входа к выходу.

Борис Цирлин и Александр Кушнеров
30.10.2019

Для опытного разработчика схем не составляет большого труда узнать знакомую схему, в каком бы виде она не была нарисована. В этой статье мы покажем, что две транзисторные схемы из патентов являются вариантом асинхронного счётного триггера (АСТ). По сравнению со стандартной схемой, в схемах из патентов отсутствуют некоторые транзисторы. Это может рассматриваться как неисправность. Мы покажем, что, если такая же неисправность возникает в стандартной схеме, она продолжает работать правильно. АСТ, реализованный только на элементах ИЛИ-НЕ [1] или только на элементах И-НЕ известен как гарвардский триггер. Оба варианта схем показаны на Рис. 1, где g7 – это индикатор завершения переходных процессов. В дальнейшем мы его рассматривать не будем. На Рис. 1 показаны также графы сигнальных переходов (STG) [2] построенные в Workcraft [3].

Рис. 1. Асинхронный счётный триггер (АСТ) и его STG.

Обратим внимание, что в обоих вариантах АСТ есть три пары элементов (g1, g2), (g4, g5) и (g3, g6), которые имеют общий вход. Транзисторные схемы элементов 2И-НЕ и 2ИЛИ-НЕ показаны на Рис. 2. Трёхвходовые элементы устроены аналогично и содержат 6 транзисторов.

Рис. 2. Транзисторные схемы элементов 2И-НЕ и 2ИЛИ-НЕ.

Возьмём два элемента 2ИЛИ-НЕ и выберем у каждого вход, где p-MOS транзистор подключён к Uпит. Соединим эти входы вместе и подключим к земле (лог. 0). Оба транзистора откроются и напряжение на их стоках будет равным Uпит. Достаточно ли этого чтобы безопасно соединить стоки и заменить два транзистора на один, как показано на Рис. 3? Нет. Нужно проверить что произойдёт если на общий вход подать лог. 1. Выходы обоих элементов соединятся с землёй, и мы будем иметь мостиковую схему из четырёх p-MOS транзисторов. Для оставшихся двух входов имеем четыре комбинации 0 и 1. Легко показать, что ни в одной из них не возникает короткого замыкания между Uпит и землёй.

Рис. 3. Два элемента 2ИЛИ-НЕ, имеющие общий вход.