Хабр Курсы для всех
РЕКЛАМА
Практикум, Хекслет, SkyPro, авторские курсы — собрали всех и попросили скидки. Осталось выбрать!
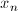 или
или  — вещественные. Поэтому формула вроде
— вещественные. Поэтому формула вроде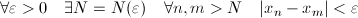
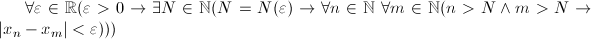
на самом деле эквивалентна такой:
ε > 0 — не надо выносить в левую часть импликации, потому что эта «область определения» не содержит вхождений других переменных, она «внешняя» по отношению к формуле.Квантификация по множеству разворачивается в культурный теоретико-множественный язык без всякой магии, то бишь в:
В этом случае, если мы перепишем более строго «ε ∈ R+», то здесь «∈» понимается как в некотором смысле тип («ε: R+»).Вроде как схема выделения в ZF вам дана аксиоматикой — тут снова нет никакой магии.
Схема выделения тут, очевидно, ни при чём — тут даже нет «переменных-множеств».Вам нужны типы, чтобы" более строго" записывать ε ∈ R+, при том что это утверждение по схеме выделения равносильно ε ∈ R ∧ ε > 0. Собственно, послание было в том, что схема выделения для всех мыслимых (мной — как профан могу что-то упускать) применений квантификации по множеству обходит ограничение о неупоминании квантифицируемой переменной в терме-множестве.
Речь идёт о том, как от матанистических «ограниченных кванторов» (на которые даже отрицания трудно навешивать) перейти к формуле с обычными логическими кванторами; это ортогонально теориям множеств.Интересно, каким языком вы будете определять квантификацию по множеству, если не языком теории множеств (естественно, не обязательно ZF). Вообще, не понимаю, что может быть неинтуитивного в разворачивании всеобщности в импликацию и существования — в конъюнкцию; одновременно, легальность оговаривания чего-то на стороне в окрестностях формулы непонятна мне.
Вам нужны типы
при том что это утверждение по схеме выделения равносильно ε ∈ R ∧ ε > 0
Вообще, не понимаю, что может быть неинтуитивного в разворачивании всеобщности в импликацию и существования — в конъюнкцию
А почему тогда не писать «ε ∈ C ∧ (ε ∈ R ∧ ε > 0)»? Это тоже равносильно «ε ∈ R+».Понятия не имею. Лично я бы так не писал, потому что это потребовало бы расширения множества аксиом комплексными числами, что, наверное, совершенно не обязательно.
Почему вместо «ε ∈ R+» должны писать «ε ∈ R ∧ ε > 0»; но при этом не пишем «m ∈ Z ∧ m > 0» вместо «m ∈ N»?Вы не обязаны писать «ε ∈ R ∧ ε > 0»; вы можете писать «m ∈ Z ∧ m > 0» вместо «m ∈ N». На всякий случай уточню, что я ни разу не знаток теории множеств и просто пытаюсь разобраться, а вовсе не спорю ожесточенно, если что, и не против прикоснуться к мудрости знатоков.
Так я её так и развернул. Неинтуитивность неразвёрнутых bounded quantifiers проявляется, например, при построении отрицания.С неинтуитивностью отрицания ограниченных кванторов я не спорю. Я не понял, почему не надо класть положительность эпсилон в импликацию слева под квантором и почему утверждение про связанную переменную «внешнее», только и всего.
Я не понял, почему не надо класть положительность эпсилон в импликацию слева под квантором и почему утверждение про связанную переменную «внешнее», только и всего.
Вам нужны типы, чтобы" более строго" записывать ε ∈ R+, при том что это утверждение по схеме выделения равносильно ε ∈ R ∧ ε > 0.
Знали бы вы, как выглядит ваша последняя фраза, у которого уровень знания математики на уровне 11 класс+.Мне не стыдно признать свою математическую безграмотность, если что, хотя я бы предпочел замечание по существу. Лично мне, да, непонятно, как с точки зрения логики можно что-то написать на стороне про связанную в формуле переменную.
Таким образом, из определения Коши можно убрать к-нулевое, или, другими словами, не бывает таких последовательностей, которые фундаментальны / не фундаментальны до какого-то номера

Как первокурсник определение Коши сократил