Comments 13
Много букв, внимательно почитаю позднее. Однако.
У нас дискретная система, N коробок по 1024 конфет, 1024 сладкоежек. Есть устойчивое равновесие - когда по N конфет у каждого. Но даже если оно недостижимо - ввиду конечности числа состояний по принципу Дирихле система рано или поздно зациклится. При этом начальное состояние не обязательно будет содержаться в финальном цикле. Т.е. после достаточно большого числа итераций провернуть фарш назад не получится.
У меня вышло мало букв, я что-то упустил?
p.s. не рассчитывайте на мой быстрый ответ - мне карма не позволяет ?
p.s.s. зато пока могу здесь добавить - я утверждаю, что открутить назад может не получиться при любом числе участников, нечетность не рулит.
Да, ниже говорится, что для возможности всё обратить важно чтобы количество количество участников было нечётным.
И что? В этом случае не возможен цикл не включающий начальное состояние? Ну, если выражаться иначе, нет состояний в которое можно прийти двумя различными путями?
Если это так, то это совсем не очевидно!
Циклы возможны, но откатив на столько же шагов получим точно то же состояние. А если количество нечётное, даже два, то даже первый шаг не обратить.
Вы, может быть, не совсем поняли о чём идёт речь. Если у нас есть состояние В, непосредственным предшественником которого является как состояние А, так и состояние Б, то как вы выберете в какое возвращаться?
Не все дискретные автоматы обратимы — та же игра Жизнь, например: вы в ней далеко не всегда сможете "мясорубку назад провернуть".
Т.е. обратимость надо обосновывать отдельно.
зато пока могу здесь добавить - я утверждаю, что открутить назад может не получиться при любом числе участников, нечетность не рулит.
Не зря статья позиционирует себя как развитие интуиции.
Вас ждёт забавное открытие. Ну, или меня, если вы хоть как-то примерно намекнёте на особые случаи, когда это не получается.
Для уточнения: после деления пополам конфет может быть не целое число, это ограничение мной не учитывается.
Получилась, на мой взгляд, и развлекательная и познавательная статья.
Я: не понял ничего, не говоря уж о развлечении
Когда-то давно было подобное на хабре
Статья классная. Свертки еще используются для "арифметических" операций над распределениями плотности вероятности. Там тоже все очень интересно получается, настолько, что на интуицию даже не стоит полагаться.
Мне тоже одно время интересовали свёртки - в том числе фурье - даже статейки накропал
https://habr.com/ru/post/597715/
Эта картинка однозначно имеет отношение к Chirp Z-transform:
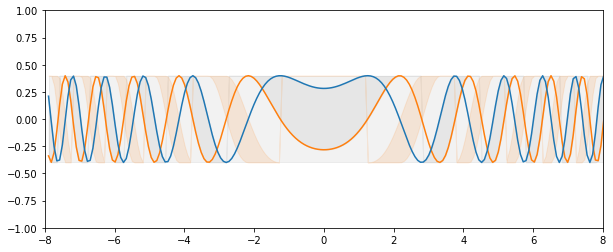
Я также слышал о Fractional Fourier transform, но не вникал в его суть для понимания того, как оно соотносится с содержанием вашей статьи.
Волновая интуиция