heinrich_wirth Oct 4 2023 at 11:51

Детекция дефектов дорожного покрытия без размеченных данных: Хакатон, LiDAR, RANSAC, ICP и 44 бесcонных часов

Medium

14 min

HackathonMachine learning*Data visualization*Algorithms*Python*

Здравствуйте, читатели Хабра! Решил активнее вкатываться в DS (хотя уже больше года в "теме" и даже нет ни одной публикации, ужас) и написать первую статью на Хабре.

Сегодня хотелось бы поделиться с вами опытом, который я получил во время недавнего хакатона. Надеюсь, статья по моей части работы окажется полезной и интересной для многих из вас.

О чем статья?

В этой статье мы рассмотрим дорожное покрытие, а именно – задачу детекции его дефектов без необходимости разметки данных. Разметка сама по себе отнимает много ресурсов у компаний, а уж разметка облака точек... можете себе представить трудоемкость и затратность денежных ресурсов.

Я расскажу о том, как мы использовали данные с LiDAR, применяли различные алгоритмы для обработки и анализа информации и какие результаты удалось достичь. Задача была нетривиальная для нашей команды так как никто не работал с облаком точек до этого и ожидали мы классические данные видеопотока, но заказчик смог удивить. В ограниченные сроки без сна и отдыха пришлось изучить библиотеки для такого типа данных и придумать новую стратегию для решения задачи.

Введение

Москва – огромный мегаполис, дороги которого каждый день перевозят миллионы автомобилей. Но с каждым годом дороги стареют, и на их поверхности появляются различные дефекты: ямы, трещины, выбоины. Эти дефекты не только ухудшают комфорт вождения, но и могут стать причиной аварий. Своевременное обнаружение и устранение таких дефектов – важнейшая задача, стоящая перед городскими службами. Но как это сделать максимально эффективно и быстро?

Задача

Целью нашего проекта стало создание алгоритма, который бы мог автоматически обнаруживать дефекты дорожного покрытия, используя данные с LiDAR – устройства, которое может сканировать дорожное покрытие с высокой точностью. Проблема состояла в отсутствии всякой разметки от заказчика.

Этапы разработки решения

Первоначальный анализ и борьба с форматом

На начальном этапе нас ждала первая "загадка" в виде данных в необычном формате - классический файл .db с вложенным бинарным кодом. Изначальные инструкции от организаторов казались простыми: использовать ROS2 для доступа к данным. Однако, практика показала, что это было далеко не так просто. Многие команды столкнулись с проблемами на этапе открытия данных, что добавило задаче еще больше интриги. После нескольких часов усилий и разбирательств, нам, наконец, удалось перевести данные в более удобный для работы формат csv. Этот этап, без сомнения, стал своего рода "фильтром" для участников хакатона, который прошли не все.

Изучение дефектов и исправление искажений

Когда казалось, что труднейшая часть задачи позади и можно приступить к основной работе, наш энтузиазм был резко остановлен снова. Визуализируя облако точек, мы столкнулись с проблемой: все точки были наклонены по оси Z, что делало их малопригодными для дальнейшего анализа.

Более наглядно видно на этом изображении. Цветом обозначается "высота" точки, то есть значение Z.

Что делать в такой ситуации? Как привести данные в "норму"? Вспомнив теорию линейной алгебры и, особенно, исследование 3D матриц поворота, я начал искать способы коррекции. Ответ нашелся благодаря алгоритму RANSAC - инструменту, позволяющему определить наилучшую плоскость по заданным точкам. С его помощью я смог выровнять наши данные, превратив искаженное облако точек в качественный датасет для дальнейшей работы. Давайте более подробно рассмотрим, как работает этот алгоритм.

RANSAC

RANSAC (Random Sample Consensus) – это итерационный метод оценки параметров математической модели на основе набора наблюдений, содержащих выбросы. При работе с облаками точек и 3D-геометрией, как в нашем случае, RANSAC часто используется для нахождения плоскостей или других геометрических объектов в данных.

Описание алгоритма:

Выборка: На каждой итерации выбирается случайное подмножество точек из исходного облака точек. Для детекции плоскости обычно выбираются три случайные точки (поскольку три точки определяют плоскость в трехмерном пространстве).
Модель: Исходя из выбранных точек, строится модель плоскости.
Консенсус: Остальные точки тестируются на соответствие этой модели. Точка считается "внутренней", если она находится на расстоянии меньше заданного порога (настраиваемый параметр) от модели плоскости.
Лучшая модель: Если текущая плоскость имеет больше "внутренних" точек, чем любая из ранее найденных плоскостей, то она становится текущей лучшей моделью. Цель- найти модель с наибольшим количеством "внутренних" точек.
Остановка: Процесс повторяется заданное количество раз или до тех пор, пока не будет найдена модель, которая удовлетворяет определенному условию (например, определенное количество "внутренних" точек).

Что такое "внутренние" точки и "порог" можно наглядно увидеть на следующем изображении в двухмерном пространстве

Математика

Плоскость в трехмерном пространстве определяется уравнением:

где [a,b,c] – нормальный вектор плоскости.

Три случайные точки могут быть использованы для определения этой плоскости.

Нормальный вектор [a,b,c] можно найти как векторное произведение векторов, соединяющих эти точки:

Затем, коэффициент d может быть найден из известной точки:

Расстояние от точки (x,y,z) до плоскости задается следующим уравнением:

$dist=\dfrac{∣ax+by+cz+d∣}{\sqrt{a^2+b^2+c^2}}$

Точки, для которых dist меньше заданного порога, считаются "внутренними".

Простая реализация для плоскости в коде

# Выбор трех случайных точек из облака точек
def random_three_points(points):
    idx = np.random.choice(points.shape[0], 3, replace=False)
    return points[idx]

# Определение параметров плоскости (A, B, C, D) на основе трех точек
def fit_plane(points):
    p1, p2, p3 = points
    # Вычисляем нормаль к плоскости как векторное произведение двух векторов на плоскости
    normal = np.cross(p3 - p1, p2 - p1)
    # Вычисляем D для уравнения плоскости
    d = -normal.dot(p1)
    return np.append(normal, d)

# Расчет расстояния от точки до плоскости
def distance_to_plane(plane, point):
    a, b, c, d = plane
    # Расстояние от точки до плоскости
    return abs(a*point[0] + b*point[1] + c*point[2] + d) / np.linalg.norm([a, b, c])

# Основная функция RANSAC для поиска наилучшей подгонки плоскости к облаку точек
def ransac_plane_fit(points, n=1000, threshold=0.05):
    best_plane = None  # Лучшая плоскость, найденная на данный момент
    best_inliers = -1  # Количество точек, близко расположенных к лучшей плоскости
    
    # Повторяем процесс n раз
    for _ in range(n):
        # Выбираем 3 случайные точки
        sample_points = random_three_points(points)
        # Получаем уравнение плоскости для этих точек
        plane = fit_plane(sample_points)
        # Считаем, сколько точек лежит близко к данной плоскости
        inliers = sum(1 for point in points if distance_to_plane(plane, point) < threshold)
        
        # Если текущая плоскость лучше предыдущей лучшей, обновляем лучшую плоскость
        if inliers > best_inliers:
            best_inliers = inliers
            best_plane = plane
    
    return best_plane

Работа нашего алгоритма на сгенерированных данных

Матрица поворота

Чтобы вращать плоскость таким образом, чтобы её нормальный вектор n смотрел вдоль оси z и сама плоскость была параллельна x и y, нужно выполнить поворот вокруг некоторого вектора поворота на определенный угол.

Нахождение вектора поворота:
Вектор поворота — это вектор, который перпендикулярен как текущему нормальному вектору n, так и оси z. Мы можем получить его, взяв векторное произведение между n и осью z:

$v_{rotation}=n×[0,0,1]$

Нахождение угла поворота:
Угол поворота θ между текущим нормальным вектором n и осью z можно найти с помощью скалярного произведения:

$cos(θ)=\dfrac{n \cdot [0,0,1]}{|n|}$ $θ=arccos(\frac{n \cdot[0,0,1]}{|n|})$

Матрица поворота
В 3D пространстве матрица поворота вокруг вектора
$v_{rotation}=[v_x,v_y,v_z]$
на угол θ задается следующим образом:

$R_z(\theta) = \begin{bmatrix} \cos(\theta) & -\sin(\theta) & 0 \\ \sin(\theta) & \cos(\theta) & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}$

Поворот
Далее просто умножаем каждую точку на матрицу поворота для исправления наших данных.

Реализация в проекте с использованием Open3D:

# Используем RANSAC для нахождения плоскости
plane_model, inliers = point_cloud.segment_plane(distance_threshold=0.1,
                                                ransac_n=3,
                                                num_iterations=4000)

# Извлекаем нормальный вектор плоскости
a, b, c, d = plane_model

plane_normal = np.array([a, b, c])

# Нормализуем вектор
plane_normal = plane_normal / np.linalg.norm(plane_normal)

# Находим вектор вращения и угол между нормалью плоскости и осью Z
axis = np.cross(plane_normal, [0, 0, 1])
axis = axis / np.linalg.norm(axis)
angle = np.arccos(np.dot(plane_normal, [0, 0, 1]))

# Создаем матрицу вращения
R = o3d.geometry.get_rotation_matrix_from_axis_angle(axis * angle)

# Применяем вращение к облаку точек
point_cloud.rotate(R, center=(0, 0, 0))

Погоня за разрешением: преодоление ограничений техники

После успешной борьбы с искажением данных, казалось бы, большая часть проблем позади. Однако наш оптимизм был преждевременным. Ожидая работать с облаком точек высокого разрешения, как обещал заказчик, нас ожидало разочарование. По утверждениям, лидар обладал возможностью собирать более 6 миллионов точек, но при практической работе стало ясно, что разрешение недостаточно для качественной детекции дефектов дорожного покрытия.

Очевидное решение - комбинировать данные из нескольких кадров для увеличения плотности точек. Но такой подход приводил бы к проблемам со смещением, особенно при движении или поворотах. Нам требовался метод, который позволил бы "склеить" кадры максимально точно и без искажений.

Исходя из этой потребности, меня поиск привел к алгоритму ICP (Iterative Closest Point). Этот метод предоставил необходимые инструменты для объединения разных облаков точек таким образом, чтобы минимизировать потенциальные ошибки и искажения. На практике, ICP дал возможность эффективно и точно совместить данные, дав достаточное разрешение для последующего анализа. Но что такое ICP и как он работает? Давайте рассмотрим этот вопрос чуть подробнее.

ICP

ICP, или Iterative Closest Point, — это алгоритм, который широко используется в области компьютерного зрения и робототехники для выравнивания и объединения двух облаков точек.

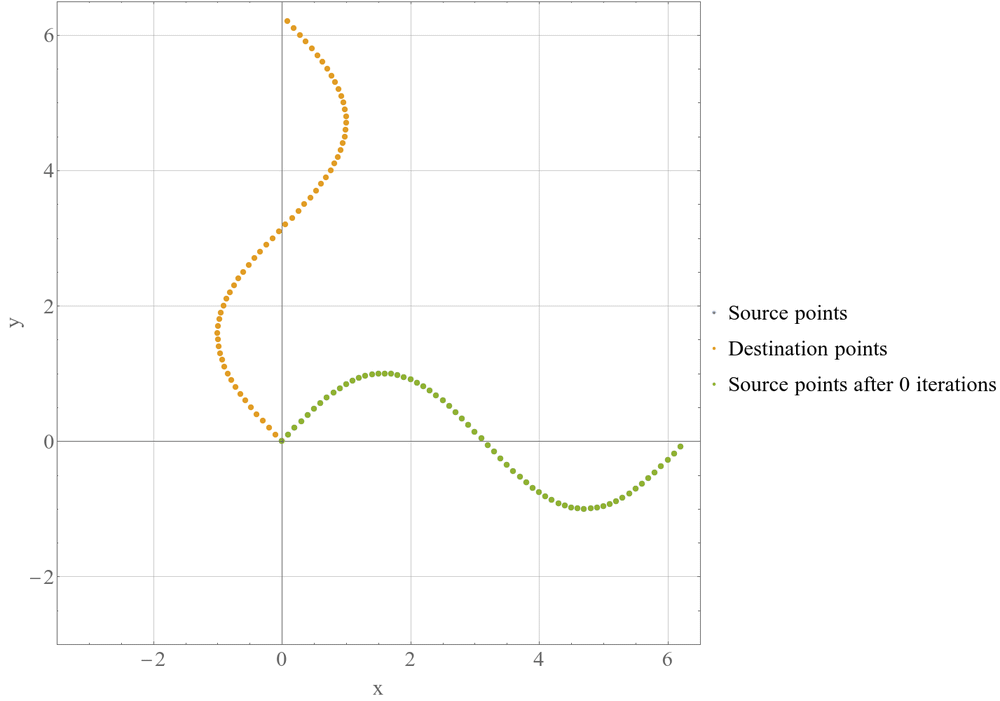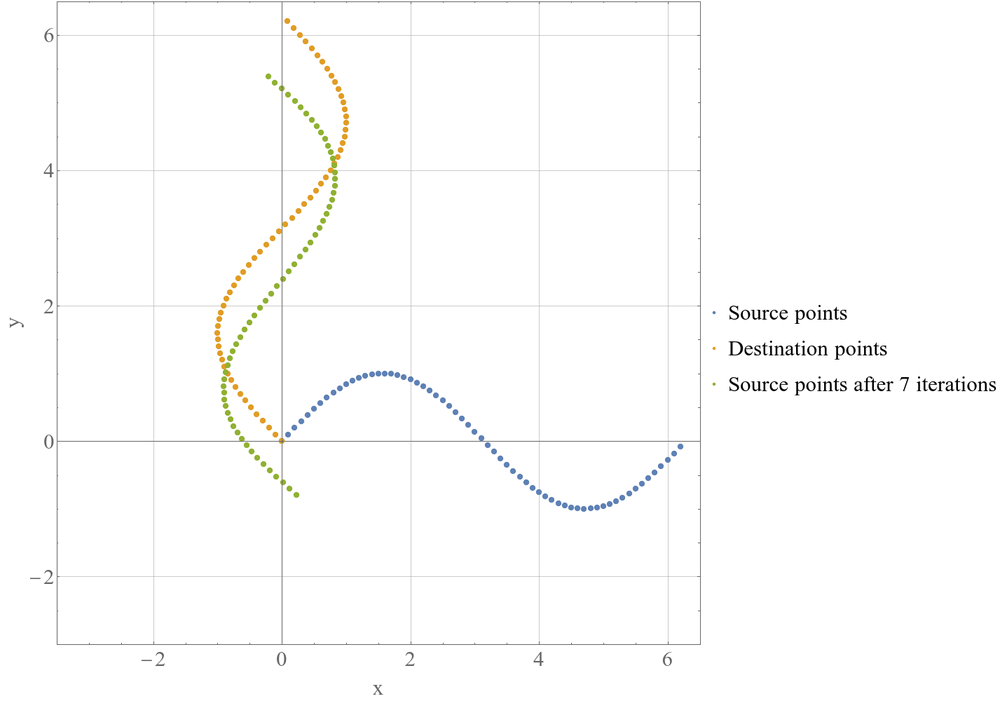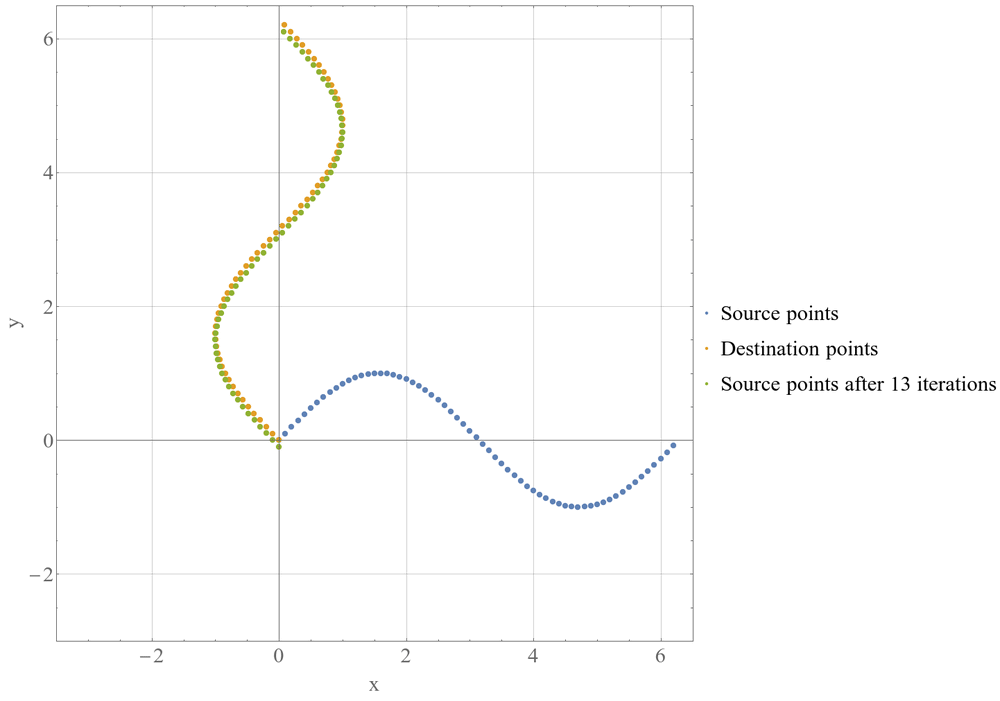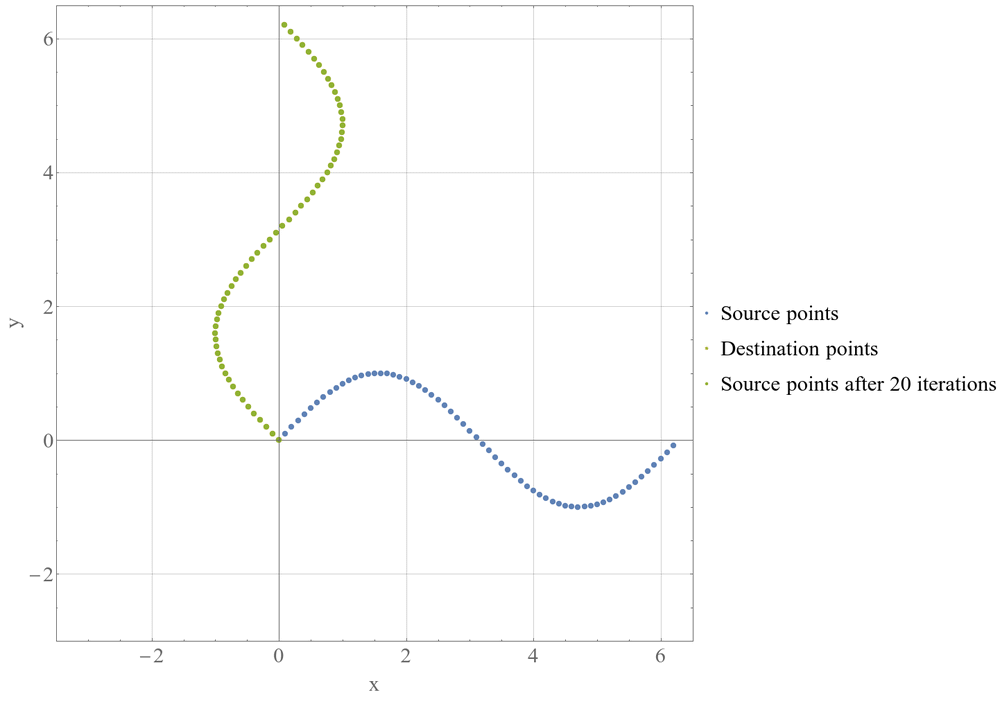
Целью ICP является минимизация расстояния между двумя облаками точек — исходным и целевым. Алгоритм последовательно корректирует положение и ориентацию исходного облака точек таким образом, чтобы максимально приблизить его к целевому.

Этапы алгоритма

Выбор соответствий: Для каждой точки в исходном облаке выбирается ближайшая точка в целевом облаке.
Минимизация ошибки: На основе выбранных соответствий рассчитывается оптимальное преобразование (сдвиг t, вращение R), минимизирующее суммарное квадратичное расстояние между точками.
Применение преобразования: К исходному облаку точек применяется рассчитанное преобразование.
Проверка сходимости: Если изменение ошибки между последовательными итерациями меньше заданного порога или достигнуто максимальное количество итераций, алгоритм завершает работу.

Пример работы алгоритма в двумерном пространстве

Математика

На этом этапе для каждой точки из одного облака (A) находим ближайшую точку в другом облаке (B). Это можно делать различными способами, например, используя NearestNeighbors из sklearn. (Работу NearestNeighbors расписывать не буду. Сейчас речь не о нем и статей про его работу достаточно)
Цель этого этапа — найти матрицу вращения R и вектор смещения t, которые оптимально совмещают облака точек.
Среднее значение
Для начала определим средние значения для двух облаков точек:
$C_A = \frac{1}{N} \sum_{i=1}^{N} a_i$ $C_B = \frac{1}{N} \sum_{i=1}^{N} b_i$
где N — количество точек в облаках.
Центрированные точки
Затем центрируем облака точек:
Матрица ковариации
Ковариационная матрица служит для измерения, насколько одно облако точек "распределено" по отношению к другому. Она создается путем умножения разности каждой точки от среднего значения в одном облаке на разность каждой точки от среднего значения в другом облаке:
SVD (Singular Value Decomposition)
SVD — это метод факторизации матрицы, который представляет ее в виде произведения трех других матриц:
$U, \Sigma, V^T$
Применяя SVD к ковариационной матрице H, мы можем получить эти три матрицы. Метод SVD находит "основные направления" данных и уровень "распространения" данных по этим направлениям.
$H = U \Sigma V^T$
Матрица вращения R
Для минимизации среднеквадратичной ошибки между двумя облаками точек и определения оптимального вращения, можно использовать матрицы U и V, полученные на предыдущем этапе:
Таким образом, матрица R представляет собой оптимальное вращение, которое можно применить к облаку точек, чтобы минимизировать разницу с другим облаком.
Вектор смещения t
После того как мы определили матрицу вращения, следующим шагом является определение вектора смещения, который оптимально сдвинет одно облако точек к другому:
t представляет собой вектор, который необходимо добавить к каждой точке в облаке A, чтобы минимизировать расстояние до соответствующей точки в облаке B, после применения матрицы вращения R.
Применяем вычисленные матрицу вращения и вектор смещения к облаку точек A, чтобы совместить его с облаком B:
Повторяем все вышеуказанные шаги до тех пор, пока не достигнем определенного условия сходимости. В нашем случае это будет разница между ошибками на последовательных итерациях или максимальное количество итераций.

Теперь давайте эту логику реализуем в коде

import numpy as np
from sklearn.neighbors import NearestNeighbors

def best_fit_transform(A, B):
    # Определение средние
    centroid_A = np.mean(A, axis=0)
    centroid_B = np.mean(B, axis=0)

    # Центрирование облака точек
    AA = A - centroid_A
    BB = B - centroid_B

    # Вычисление ковариационной матрицы H
    H = np.dot(AA.T, BB)

    # SVD
    U, _, Vt = np.linalg.svd(H)
    R = np.dot(Vt.T, U.T)

    # Определение смещения
    t = centroid_B.T - np.dot(R, centroid_A.T)

    return R, t

def icp(A, B, max_iterations=20, tolerance=1.0):
    # Начальное приближение
    prev_error = 0
    for i in range(max_iterations):
        # Нахождение ближайших точек
        neighbors = NearestNeighbors(n_neighbors=1).fit(B)
        distances, indices = neighbors.kneighbors(A)
        B_matched = B[indices[:, 0]]

        # Определение матрицы преобразования
        R, t = best_fit_transform(A, B_matched)

        # Применение матрицы преобразования к A
        A = np.dot(A, R) + t

        # Вычисление ошибки
        mean_error = np.mean(distances)
        if np.abs(prev_error - mean_error) < tolerance:
            break
        prev_error = mean_error

    return R, t

Фильтрация данных и концентрация на дороге

После успешной коррекции данных, перед нами стояла новая задача: выделить из полученного облака точек лишь те, которые соответствуют дорожному покрытию.

Основная идея моего подхода заключалась в том, чтобы использовать статистику и гистограммы. Исходя из того, что дорожное покрытие представляет собой наибольшую по плотности область в облаке точек, можно было попытаться группировать точки по высоте (координата Z) и определить наиболее плотную область.

Для этой цели были выполнены следующие шаги:

Извлечение координат Z из облака точек.
Определение диапазона Z-координат для дальнейшего разделения на интервалы.
Создание гистограммы по высоте с использованием 40 корзин.
Подсчет числа точек в каждой корзине для определения наиболее плотного интервала.
Фильтрация облака точек таким образом, чтобы оставить только те точки, которые попадают в наиболее плотный интервал по Z-координате.

Результатом этого подхода стало новое облако точек, где основное внимание сосредоточено на дорожном покрытии. Этот метод позволил мне быстро и эффективно обработать данные, учитывая ограниченное время, которое было выделено на хакатон.

Пример кода для реализации логики

def filter_road_points(point_cloud):
    # Преобразование облака точек в массив numpy
    points_cloud = np.asarray(point_cloud.points)
    
    # Извлечение Z-координаты
    z_coordinates = points_cloud[:, 2]
    
    # Определение границ Z-координаты
    z_min = np.min(z_coordinates)
    z_max = np.max(z_coordinates)
    
    # Создание 40 корзин для разделения Z-координаты
    num_buckets = 40
    buckets = np.linspace(z_min, z_max, num_buckets + 1)
    
    # Группировка точек по корзинам на основе Z-координаты
    bucket_indices = np.digitize(z_coordinates, buckets)
    
    # Подсчет количества точек в каждом корзине
    counts = np.bincount(bucket_indices)
    
    # Нахождение корзины с наибольшим количеством точек
    max_count_idx = np.argmax(counts)
    lower_bound = buckets[max_count_idx - 1]
    upper_bound = buckets[max_count_idx]
    
    # Фильтрация точек на основе найденного интервала Z-координаты
    filtered_points_array = points_cloud[(points_cloud[:, 2] >= lower_bound) & (points_cloud[:, 2] <= upper_bound)]
    
    # Создание нового облака точек из отфильтрованных точек
    new_point_cloud = o3d.geometry.PointCloud()
    new_point_cloud.points = o3d.utility.Vector3dVector(filtered_points_array)
    
    return new_point_cloud

Детекция зоны высокой плотности

После успешного выделения дорожного покрытия, следующим этапом было определение оптимальной зоны для поиска дефектов. Исходя из логики работы беспилотных автомобилей, мы пришли к выводу, что наилучшая зона для детекции дефектов — это область непосредственно вокруг беспилотника, где плотность сбора данных максимальна.

Чтобы выявить эту область и сосредоточить усилия именно на ней, я провел следующую процедуру:

Сэмплирование: из общего массива точек был взят случайный поднабор, составляющий 10% от всех точек. Это позволило сократить объем данных для последующего разбиения на кластеры.
Кластеризация: на сэмплированных данных был применен метод DBSCAN для выявления групп точек на основе их пространственной близости. Данный метод позволяет выявить кластеры точек на основе заданных параметров: радиуса окрестности (eps) и минимального числа точек в окрестности для формирования кластера.
Присвоение меток: после кластеризации на подмножестве точек, метки кластеров были присвоены всем остальным точкам с помощью метода ближайших соседей (KD-дерево).
Фильтрация данных: на основе присвоенных меток выделил кластер с наибольшим числом точек — это и стало областью максимальной плотности вокруг беспилотника.

В результате этой процедуры перед нами оказалась выделенная зона с наивысшей плотностью точек, где и предполагается наибольшая вероятность наличия дефектов дорожного покрытия.

Пример реализации в коде

def nearest_neighbors_kdtree(kdtree, points, k=1):
    """
    Находит индексы ближайших соседей для массива точек.

    :param kdtree: KDTreeFlann объект
    :param points: массив точек размером (N, 3)
    :param k: количество ближайших соседей для поиска
    :return: массив индексов ближайших соседей размером (N,)
    """
    nn_indices = []
    for point in points:
        _, idx, _ = kdtree.search_knn_vector_3d(point, k)
        nn_indices.append(idx[0])
    return np.array(nn_indices)

# Загружаем облако точек
points_cloud = np.asarray(OUR_POINTS_CLOUD)

# Сэмплирование
sample_indices = np.random.choice(points_cloud.shape[0], size=int(points_cloud.shape[0]*0.1), replace=False)
sampled_points = points_cloud[sample_indices]

# Кластеризация
sample_point_cloud = o3d.geometry.PointCloud()
sample_point_cloud.points = o3d.utility.Vector3dVector(sampled_points)
labels = np.array(sample_point_cloud.cluster_dbscan(eps=0.1, min_points=20, print_progress=True))

# Присвоение меток оставшимся точкам
kdtree = o3d.geometry.KDTreeFlann(sample_point_cloud)
all_point_labels = labels[nearest_neighbors_kdtree(kdtree, points_cloud)]

Итак, область с высокой плотностью точек, представляющая дорожное покрытие, была успешно выделена. Следующим этапом нашей работы стала детекция дефектов, в частности глубоких ям на дороге.

Для решения этой задачи я применил статистический подход. Исходя из предположения, что большинство точек дороги представляют собой ровное покрытие, точки, представляющие ямы, будут являться статистическими выбросами в распределении высоты точек.

Вычисление статистик: Для начала, были рассчитаны основные статистики по Z-координатам — среднее значение и стандартное отклонение.
Определение порога для детекции ям: Используя правило "4 сигм", был установлен порог для выбросов. Точки, Z-координата которых отклоняется от среднего более, чем на 4 стандартных отклонения вниз, считаются потенциальными дефектами.
Группировка дефектов: Для того чтобы отфильтровать случайные выбросы и выделить области с настоящими ямами, был применен метод кластеризации DBSCAN. Этот метод позволяет группировать близко расположенные точки, представляющие собой одну яму, в отдельные кластеры.
Вывод результатов: После успешной кластеризации, координаты центра каждого кластера (ямы) выводятся на экран, представляя собой точное местоположение дефекта.

Пример реализации в коде

def detect_potholes(largest_cluster_points):
    #Вычисление статистик
    z_coords = largest_cluster_points[:, 2]
    mean_z = np.mean(z_coords)
    std_dev = np.std(z_coords)
    
    # Определение порога для детекции ям
    threshold = mean_z - 4 * std_dev
    
    # Выбираем точки, которые отклоняются на 4 сигмы от среднего
    outliers = [point for point in largest_cluster_points if point[2] < threshold]
    
    # Группировка дефектов
    # Создание облака точек для выбросов
    outliers_cloud = o3d.geometry.PointCloud()
    outliers_cloud.points = o3d.utility.Vector3dVector(outliers)
    
    # Применение DBSCAN для идентификации кластеров среди выбросов
    with o3d.utility.VerbosityContextManager(o3d.utility.VerbosityLevel.Debug) as cm:
        labels = np.array(outliers_cloud.cluster_dbscan(eps=0.06, min_points=3, print_progress=True))
    
    # Вывод результатов
    potholes_centers = []
    for cluster_id in np.unique(labels):
        if cluster_id == -1:
            continue
        cluster_points = np.array(outliers_cloud.points)[labels == cluster_id]
        average_latitude = np.mean(cluster_points[:, 0])
        average_longitude = np.mean(cluster_points[:, 1])
        average_altitude = np.mean(cluster_points[:, 2])
        potholes_centers.append((average_latitude, average_longitude, average_altitude))
        print(average_latitude, average_longitude, average_altitude)
    
    return potholes_centers

Последующая пост обработка убирает множественное детектирование одного и того же дефекта, оставляя лишь одно значение координат. Таким образом, благодаря комбинации статистических методов и методов кластеризации, нам удалось успешно детектировать глубокие ямы на дороге и записывать координаты беспилотника в данный момент. Такие данные могут быть крайне полезны для коммунальных служб, занимающихся ремонтом дорог.

Отработка и размышления

Заключая свою статью, могу сказать, что проект оставил после себя кучу впечатлений. Каждый этап работы принес свои уроки. Даже не верится, что столько всего смог вспомнить, изучить и реализовать в коде.

Однако, как и в любом хакатоне, не все прошло гладко. Мы не успели реализовать веб-интерфейс и визуализировать результаты на карте. На данный момент, алгоритм записывает координаты беспилотника, а хорошо бы вычислять именно координаты ям, но на это у меня просто не хватило времени. Пришлось выдавать результат менее точными. Плюс, в процессе презентации нашего решения, я чувствовал, что мы могли бы гораздо глубже раскрыть наш подход. В итоге это отразилось на нашей позиции — 7-е место. Не первое, конечно, но и не последнее.

Всё же, данный опыт стал неоценимым. Это был отличный повод освежить свои знания в математике и познакомиться с новыми методами обработки данных. Если статья вам понравится, есть и другие интересные моменты из моей практики. К примеру, не так давно мы с моей новой командой заняли второе место в другом соревновании где тоже была проблема с данными (куда же без проблем от заказчика). Но об этом — в следующий раз!

Tags:

Hubs: