Скажу сразу: как бы мне этого ни хотелось, квантовая телепортация не позволит перенести мою бабушку из деревни в мою квартиру. Бабуля знает, что мне нравятся всякие квантовые штуки, и решила вместо денег и носков отправить мне на день рождения квантовое состояние. Здесь мы поговорим о другом — передаче квантовой информации.
Это вторая статья из серии о квантовом программировании. Предполагается, что читатель уже знаком с первой частью.
К сожалению, отправить кубит ни по электронной почте, ни посылкой нельзя. Они передаются по специальным квантовым каналам, а в деревне и Интернет-то появился совсем недавно.
Но, может быть, бабушке удастся передать квантовую информацию по классическому каналу связи (например, через Интернет или телефонную линию)? Проблема заключается в том, что диапазон возможных значений квантового состояния непрерывен, поэтому для его точного описания потребуется бесконечное количество классических бит. Моя бабушка — весьма занятой человек, и у нее нет времени набирать столько бит.
Она уже начала терять всякую надежду, и тут я говорю: «Бабуль, все в порядке». Помнишь, мы в прошлую среду за чаем смастерили состояние Белла? Передать квантовое состояние можно через него! Такая передача квантового состояния с использованием классических каналов связи и называется квантовой телепортацией. Мы постараемся разобраться, как она работает — в теории и в коде.
Чтобы все описанное ниже сработало, мы с бабушкой должны подготовить состояние Белла: перевести ее кубит |G⟩ и мой кубит |F⟩ в состояние запутанности. Я расстаюсь с бабушкой, но свой кубит (половину состояния Белла) беру с собой. Наши кубиты будут находиться в состоянии запутанности вне зависимости от того, какое расстояние их разделяет — несколько километров или несколько миллиардов световых лет.
Помните, мы обсуждали замечательное свойство запутанных состояний — связанность результатов измерений соответствующих кубитов? Если бабушка измерит состояние своего кубита, это скажется на моем кубите (вне зависимости от расстояния). Ниже мы будем активно использовать это свойство.
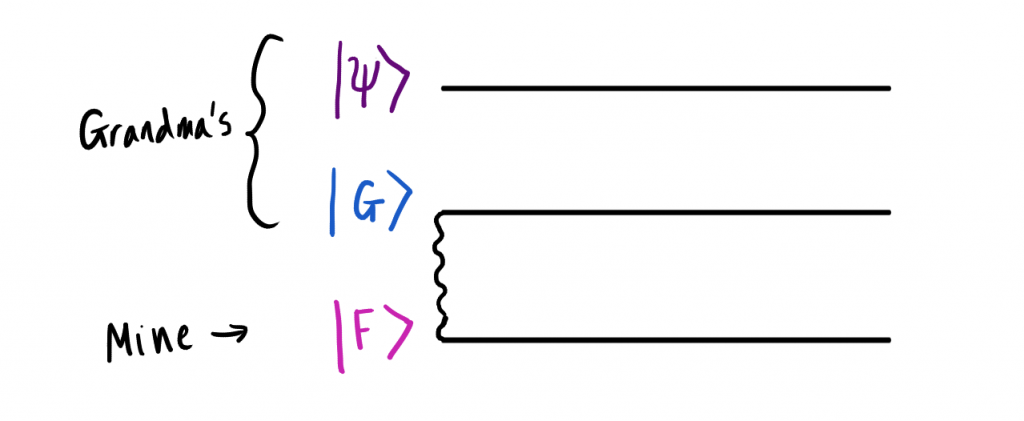
Исходное состояние будем описывать с помощью приведенной выше диаграммы. В верхнем левом углу находится предмет всех наших стараний — кубит, который бабушка хочет мне отправить. Он находится в неизвестном состоянии, которое можно представить следующим образом:
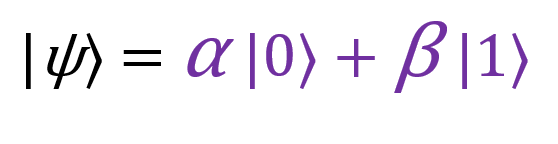
Кроме того, в ее распоряжении находится кубит |G⟩, который, как мы только что обсуждали, запутан с моим кубитом, |F⟩ (эта их связь показана волнистой линией). Теперь два кубита находятся в состоянии Белла, которое описывается формулой
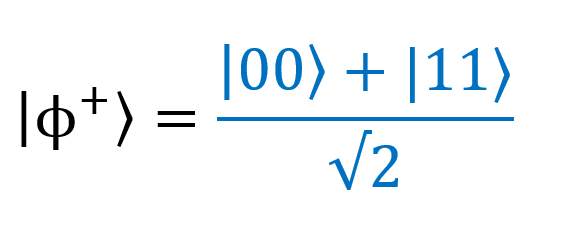
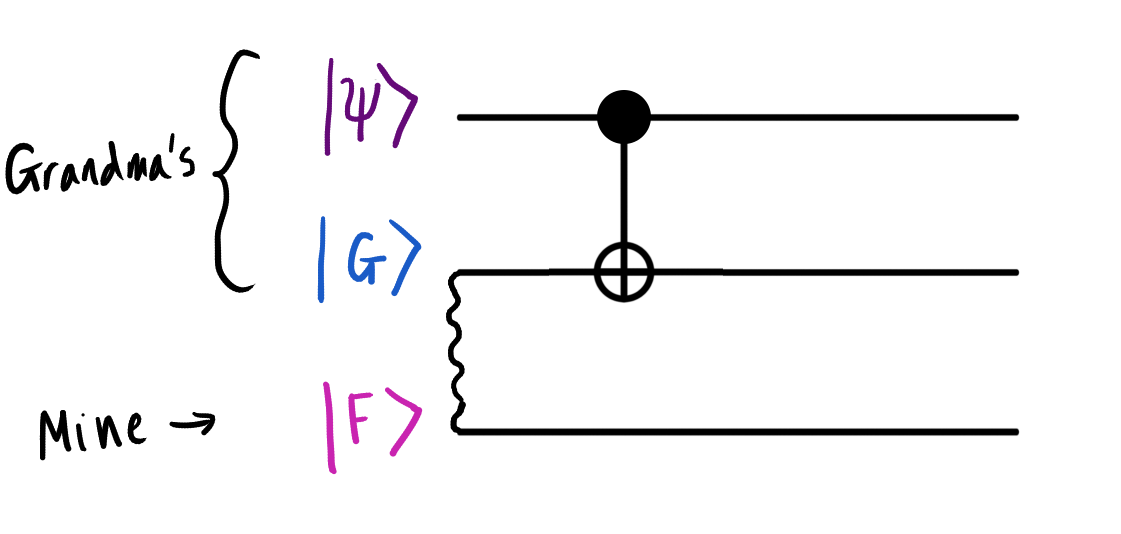
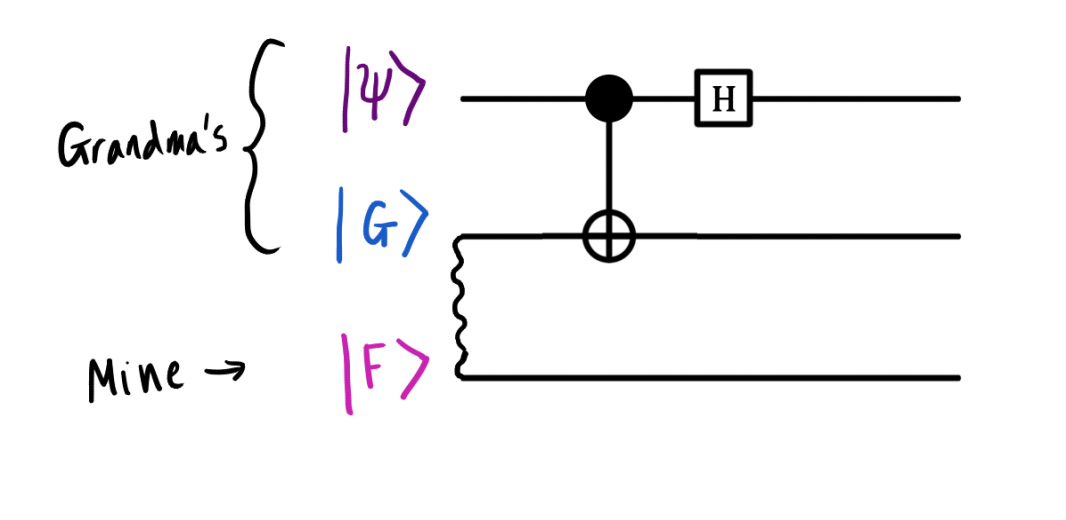
Вначале мы запутаем бабушкин кубит |G⟩ с состоянием |ψ⟩. Скоро поймете зачем. В предыдущей статье мы узнали, что два кубита можно запутать с помощью схемы, состоящей из вентиля CNOT и вентиля Адамара. Давайте посмотрим, как этот процесс представляется с помощью квантовой цепи.
[Чтобы лучше понимать эти обозначения на диаграммах квантовых цепей, рекомендую вкратце ознакомиться со статьей Квантовые цепи и вентили — вводный курс.]
Если добавить вентиль CNOT, схема принимает следующий вид. Состояние, которое подается на вход CNOT, можно записать как |ψ⟩|G⟩, где первый вход соответствует верхнему проводу, второй — среднему. Если подставить определения |ψ⟩ и |G⟩, получим:
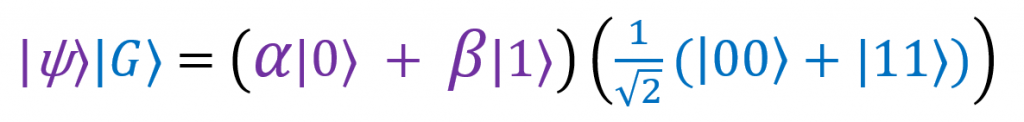
Раскроем скобки:
Таким образом, на вход подается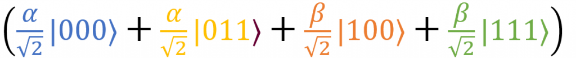
. Каждое из этих слагаемых проходит через вентиль CNOT. В первой статье мы видели, как действует вентиль CNOT и как он обрабатывает два кубита. Самые внимательные читатели уже заметили, что все наши слагаемые — |000〉, |011〉, |100〉 и |111〉 — состоят из трех кубитов. В этом случае в роли управляющего кубита используется первый, а управляемым является второй (см. ниже).
Когда управляющий кубит равен |1〉, значение управляемого кубита меняется на противоположное. Таким образом, CNOT превращает набор кубитов |100〉 в |110〉, а |111〉 — в |101〉. Все другие состояния остаются прежними.
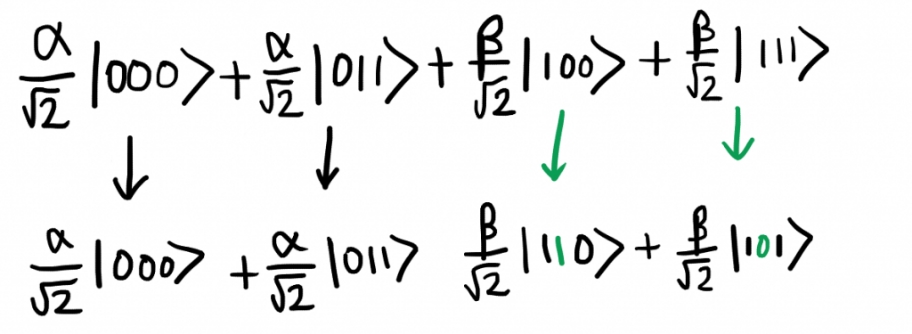
Это значит, что состояние трех кубитов после вентиля CNOT будет описываться следующим выражением: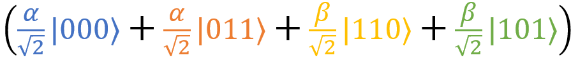
.
Второй этап запутывания кубита |G⟩ с состоянием |ψ⟩ — применение вентиля Адамара к первому кубиту. Вот как это выглядит на диаграмме квантовой цепи:
Напомню, что вентиль Адамара преобразует |0〉 и |1〉 в состояния
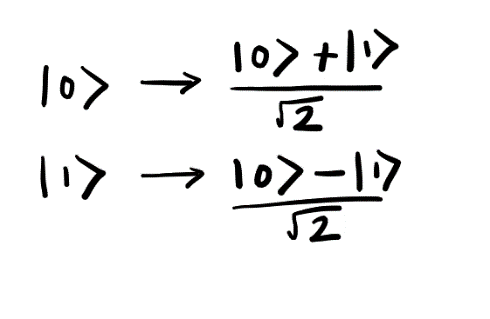
После вентиля CNOT кубиты находились в состоянии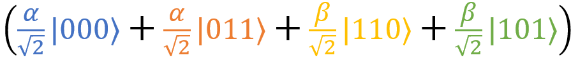. Применим вентиль Адамара к первому кубиту каждого слагаемого. Результат выглядит довольно неаккуратно:
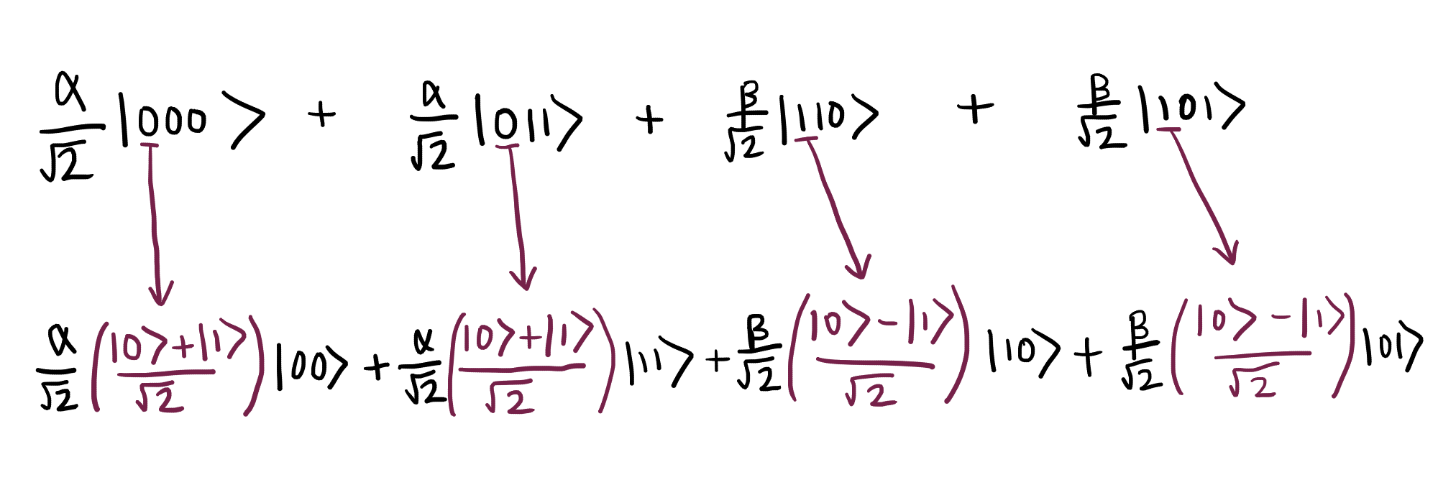
Итак, мы получили
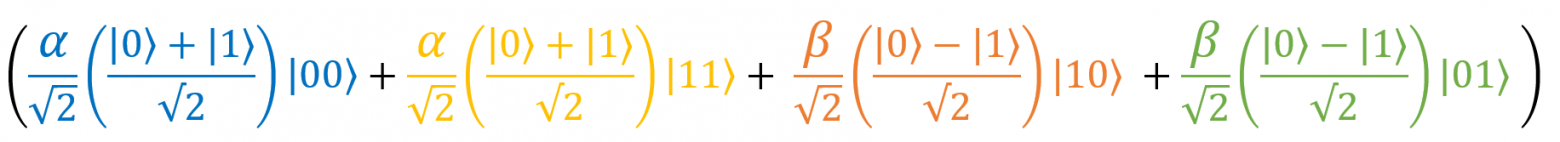
Давайте немного причешем нашу формулу. Как можно заметить, в первом слагаемом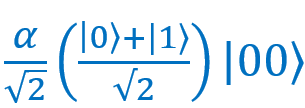
есть две дроби со знаменателем √2. Перемножим их:
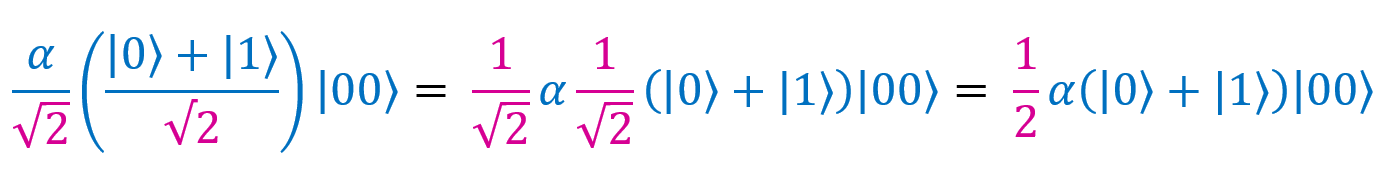
Если применить аналогичную операцию к другим слагаемым, получим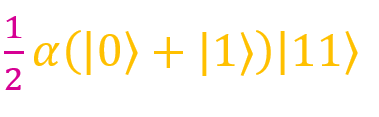
, 
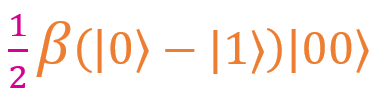и 
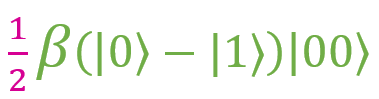. Как можно заметить, у каждой дроби есть множитель 1/2. Если вынести его за скобки, получим:
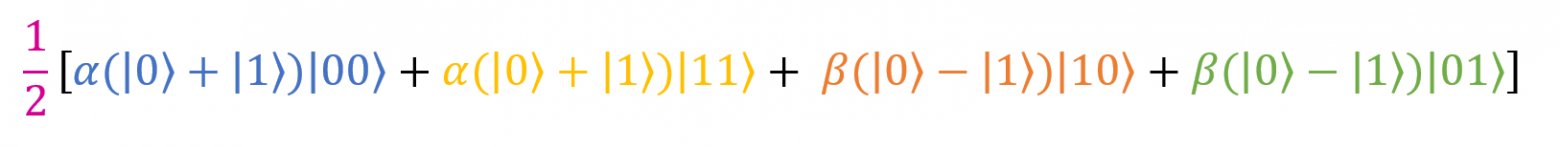
Выглядит уже лучше. Теперь раскроем скобки (это упростит нам работу на следующем этапе). В качестве примера я приведу выкладки для слагаемого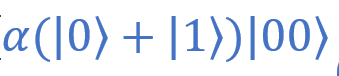
.
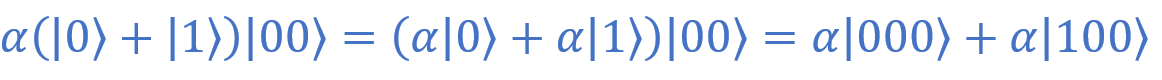
Остальные «читателю предлагается сделать в качестве упражнения». Если честно, я такие заманчивые предложения обычно игнорирую. Вот как будут выглядеть оставшиеся слагаемые, если раскрыть скобки:
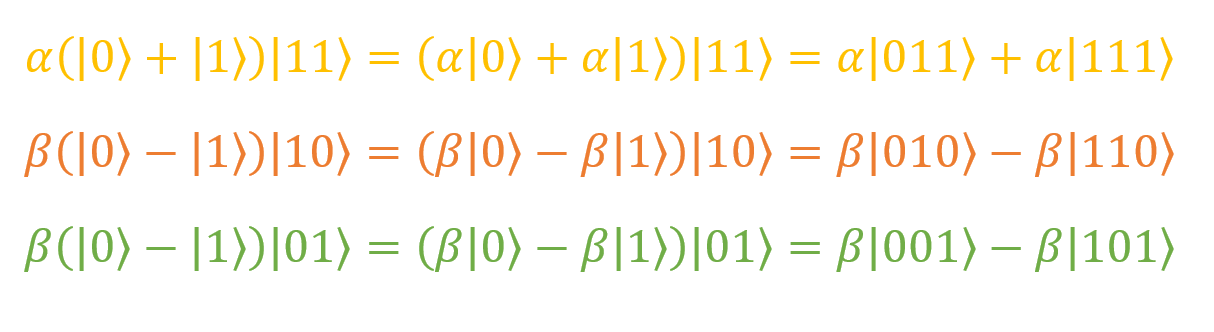
Их сумма равна
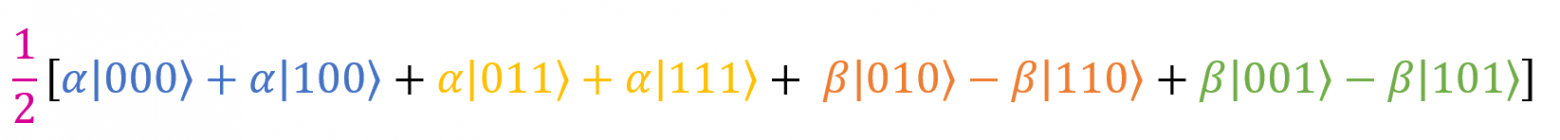
Итак, мы запутали бабушкин кубит |G⟩ с кубитом |ψ⟩. Теперь измерим их. Но перед этим результаты нужно привести к виду, более удобному для понимания.
Это последний раз, честное слово. Вот все возможные результаты измерения первого и второго кубита: 00, 01, 10, 11. Пока мы не знаем, каким в каждом из этих случаев будет наш третий кубит. Сгруппируем слагаемые так, чтобы понять, в каком состоянии будет находиться третий кубит, а именно мой кубит |F⟩.
Пока наш результат выглядит так:
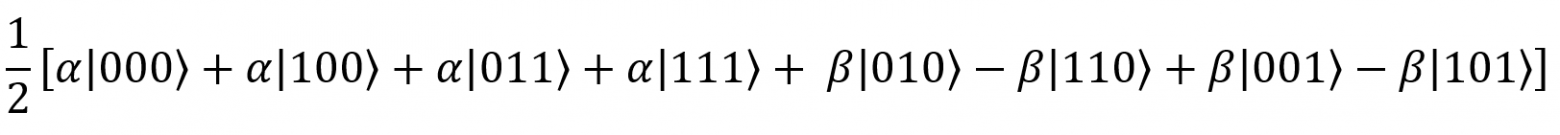
Выделим первый и второй кубит каждого слагаемого:
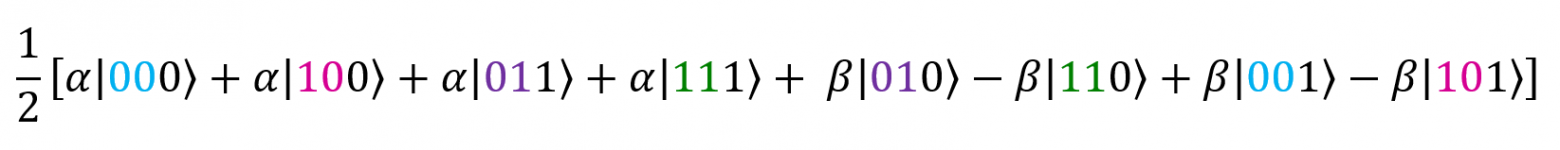
Рассмотрим случаи, в которых первый и второй кубит равны |00〉. Им соответствуют слагаемые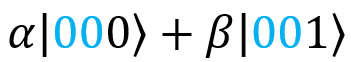
. Их можно преобразовать так:
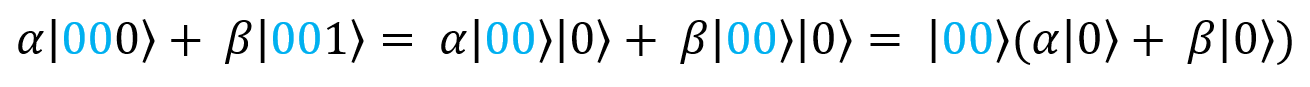
То же самое можно сделать для случаев |01〉, |10〉 и |11〉.
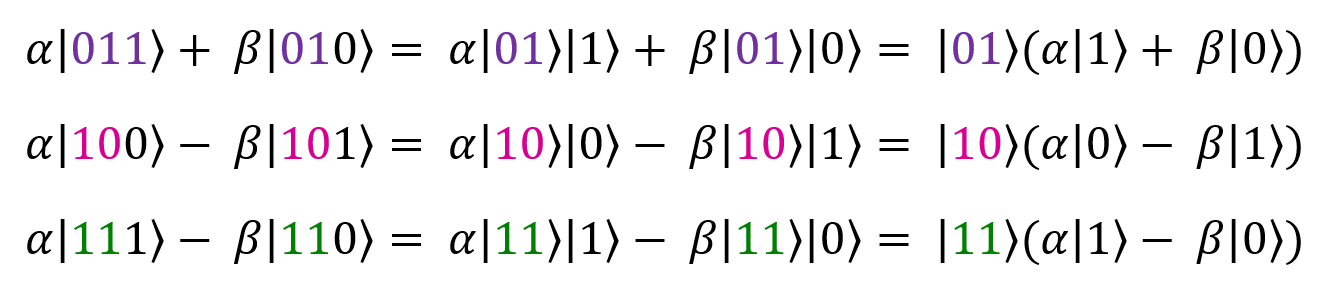
После преобразования выражение принимает следующий вид:
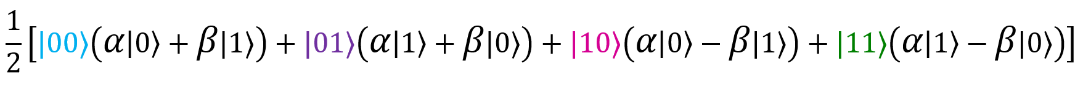
Отлично.
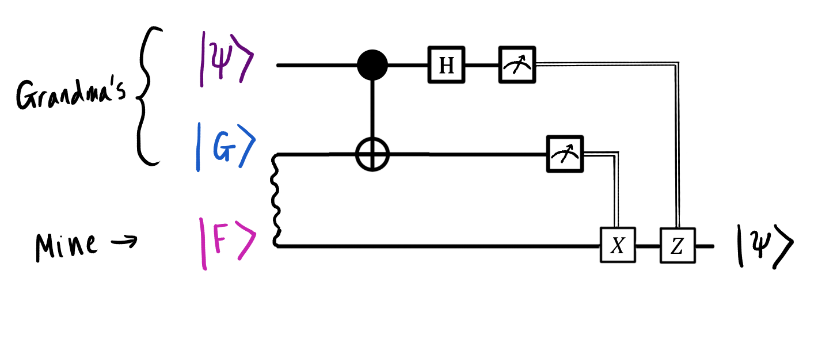
Так выглядит наша цепь с добавленными символами измерения. Обратите внимание на двойные черты после символов измерения. Они соответствуют переносу классических битов, которые и являются результатами измерений.
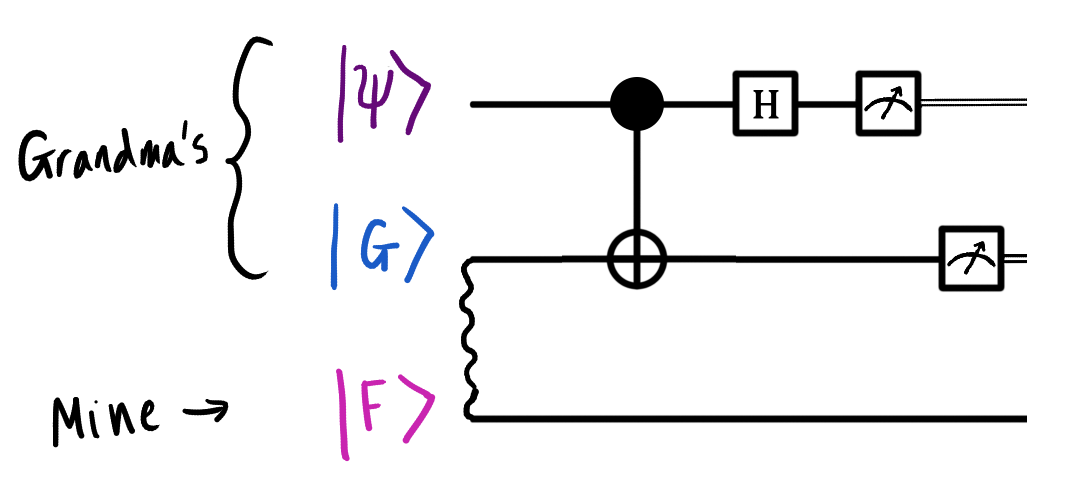
Моя бабушка также измеряет свои два кубита, |G⟩ и |ψ⟩. Как мы уже говорили, всего возможно четыре результата измерения: 00, 01, 10 или 11. При измерении кубита суперпозиция его состояний коллапсирует. Предположим, мы измерили состояние первого кубита |ψ⟩ и получили 0. Суперпозиция коллапсирует, и у нас остаются только те слагаемые, которые согласуются с таким результатом измерения (0), то есть следующие:
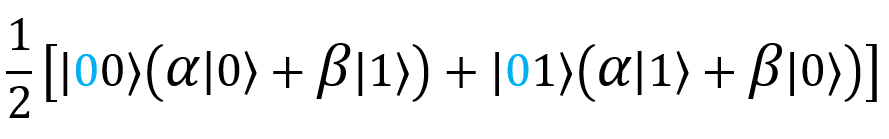
Предположим теперь, что мы измерили состояние второго кубита, |G⟩, и получили 0. Суперпозиция коллапсирует. Остается единственное слагаемое, которое согласуется с обоими результатами измерения (0 и 0), то есть следующее:
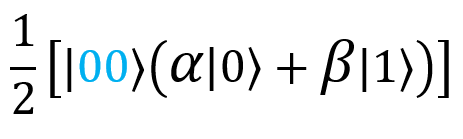
Теперь мы знаем, в каком состоянии находится третий кубит (то есть мой кубит |F⟩): в состоянии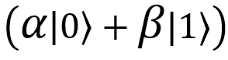
.
Что, если бы в результате измерения мы получили 01? Вернемся к нашему приведенному результату:
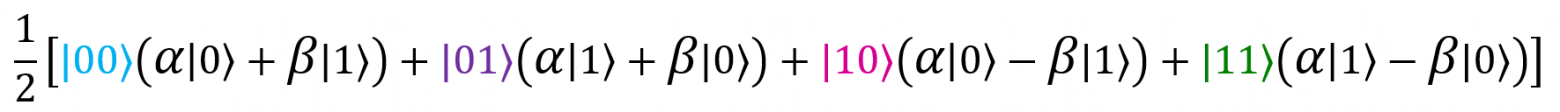
Рассуждая по аналогии, мы поймем, что единственное слагаемое, которое соответствует результату измерения 01 —
, а значит, мой кубит должен находиться в состоянии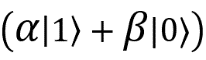 
. Если после измерений бабушка получила результат 10, то я знаю, что третий кубит в состоянии 
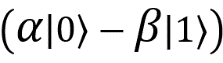, а если она получила 11, то третий кубит равен 
.
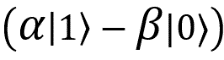Этот результат можно представить в виде таблицы:
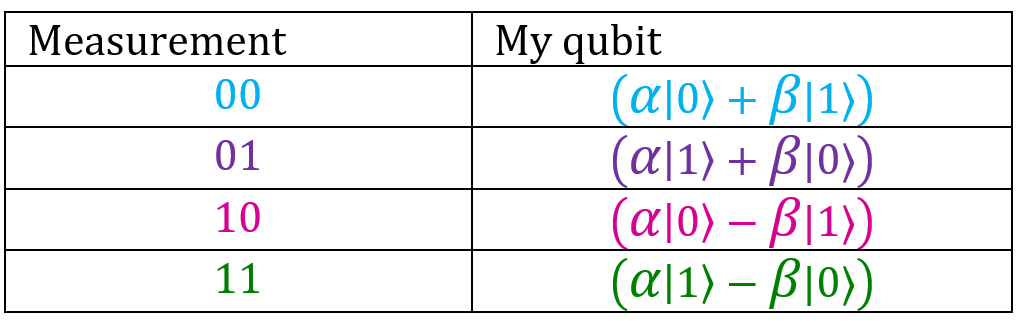
Мы остановились на том, что бабушка измерила состояние своих двух кубитов, позвонила мне и рассказала о результате, так что я знаю состояние моего кубита. Помните, что неизвестное состояние, с которого мы начали, |ψ⟩, было равно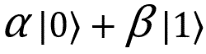
. Нам нужно применить к моему кубиту определенные операции, чтобы привести его в это состояние — в состояние, которое мне хотела отправить бабушка (в противном случае я получу нечто совсем иное).
Сейчас сделать это будет просто. Взгляните на таблицу выше. Если результат измерений 00, а мой кубит находится в состоянии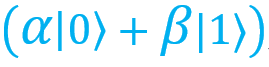
, то выполнять какие-либо операции над ним не нужно — он уже в состоянии |ψ⟩. Это самый простой случай.
Если результат измерений 01, то мой кубит находится в состоянии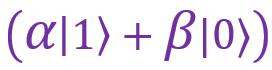
. Если сравнить его с состоянием |ψ⟩, станет понятно, что нам нужно поменять местами коэффициенты при |0〉 и |1〉. Для этого просто пропустим мой кубит через вентиль NOT, то есть вентиль X, и получим нужный результат 
.
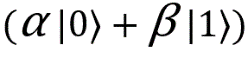При результате измерений 10 мой кубит находится в состоянии
. Сравним его с |ψ⟩. У нас есть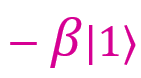 
, а нужно 
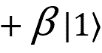. Чтобы сделать желаемое действительным, применим вентиль Z, который меняет знак.
И последний вариант — 11. В этом случае мой кубит находится в состоянии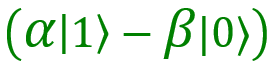
. Здесь нужно поменять местами коэффициенты при |0〉 и 1〉, а также знак при 
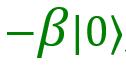. Таким образом, мой кубит нужно пропустить через вентиль X, а потом через Z. Тогда мы получим нужный результат, 
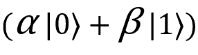. Внесем эти операции в таблицу.
Обратите внимание: если первый бит результата измерения равен 1, то мы применяем вентиль Z, а если второй бит равен 1, то применяем вентиль X. Окончательный вариант цепи показан ниже. Мы добавили вентиль Z, используя верхний провод в качестве управляющего, и вентиль X, для которого управляющим будет второй провод. Управляемым при этом будет мой кубит (потому что именно его нужно обработать с помощью вентилей).
Итак, мы показали, что бабушке достаточно передать всего два классических бита (а именно результаты измерения состояний кубитов |G⟩ и |ψ⟩), чтобы мы могли узнать неизвестное до этого состояние кубита. Благодаря явлению квантового запутывания информация от бабушки помогает узнать значения коэффициентов α и β. При этом нам удалось обойтись без канала квантовой связи. Поэтому такой метод называется квантовой телепортацией.
Итак, мы немного разобрались в теории квантовой телепортации. Пора переходить к коду!
Если на каком-либо шаге вам понадобится помощь, готовый код доступен здесь (просто клонируйте или скачайте репозиторий, откройте файл QuantumTeleportation.sln в Visual Studio и переходите к этапу 5).
Создайте в Visual Studio новый проект типа «Приложение Q#» и присвойте ему какое-нибудь простое и понятное название — например, QuantumTeleportation.
Загрузите копию кода с примерами квантовых вычислений на свой компьютер. Для этого клонируйте или скачайте репозиторий.
Теперь нужно заменить весь код в файле Operation.qs на код из файла TeleportationSample.qs, который находится в разделе Quantum > Samples > Teleportation здесь.
Замените весь код в файле Driver.cs на содержимое файла Program.cs.
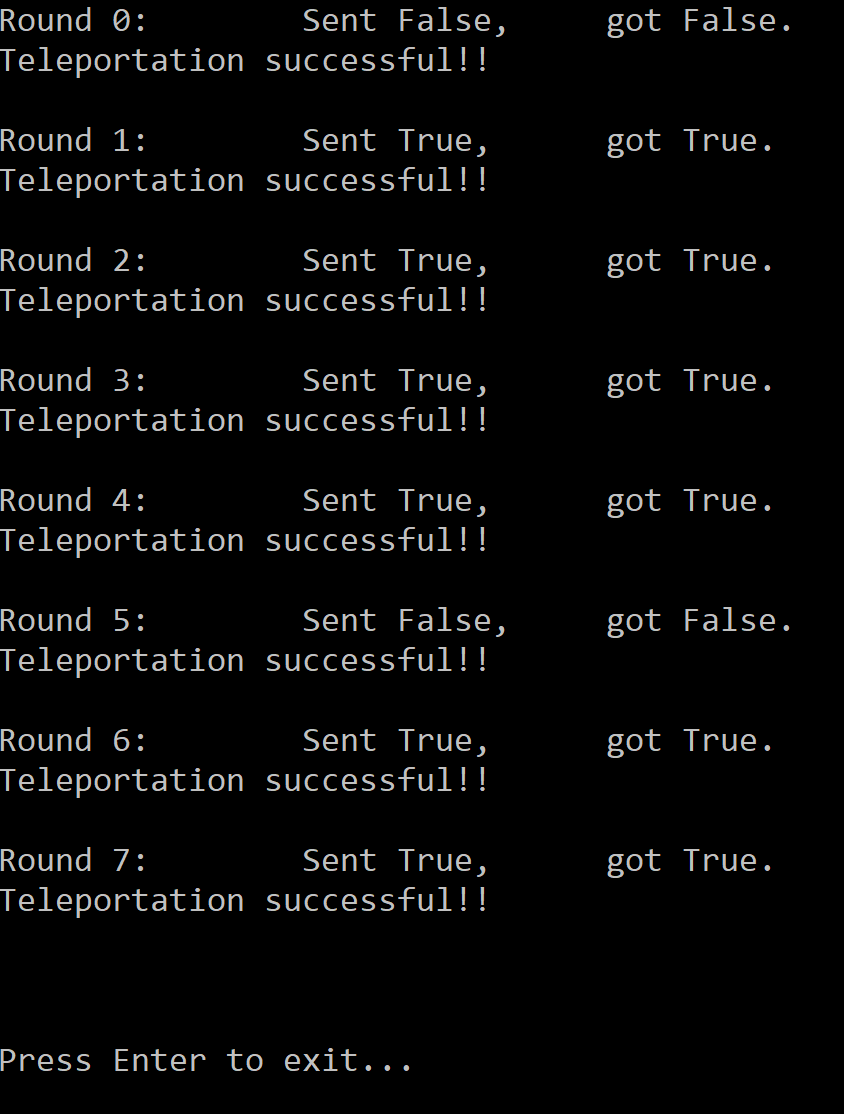
Нажмите на кнопку «start», чтобы запустить код. На экран будут выведены результаты для итераций 0–8. Они должны выглядеть примерно так:
На самом деле вы сможете в нем разобраться и без моей помощи — код замечательно прокомментирован. Мы просто сопоставим его с теорией, разобранной выше, — это будет несложно.
В первой части статьи мы говорили о трех кубитах: кубит в неизвестном состоянии |ψ⟩ и два кубита в состоянии Белла (один у бабушки, второй у меня). Этим трем кубитам в операции Teleport (Телепортация) соответствуют кубиты msg (неизвестное состояние, которое мне отправляет бабушка), here (кубит у бабушки) и there (мой кубит F, где |ψ⟩ — пересылаемое состояние).
Как уже обсуждалось, мы с бабушкой заранее подготовили пару кубитов в состоянии Белла. Один из них находится у бабушки, второй — у меня. Поэтому в самом начале нам нужно запутать ее кубит, который называется here, с моим, there. В коде для этого используются вентиль Адамара и вентиль CNOT:
Воспользуемся нашей диаграммой цепи. Я буду добавлять на нее обозначения по мере их появления в коде.
Повторяя операции, описанные в начале статьи, мы запутываем кубит бабушки here с неизвестным квантовым состоянием msg. Вентиль CNOT и вентиль Адамара на диаграмме соответствуют следующим строкам кода:
Затем мы измерили первый и второй кубиты, msg и here. О результатах именно этих измерений бабушка сообщила мне по телефону. Этим событиям соответствуют условия оператора if:
Как мы обсуждали в конце первой части этой публикации, после получения результатов измерения нужно изменить состояние моего кубита так, чтобы оно соответствовало кубиту |ψ⟩, то есть msg. Как мы говорили, если результат измерения первого кубита равен 1, то мой кубит (there) нужно пропустить через вентиль Z. Эта операция показана выше. Если результат измерения второго кубита равен 1, то мой кубит нужно пропустить через вентиль X.
Готово! Теперь мой кубит находится именно в том состоянии, которое мне хотела передать бабушка.
Давайте подумаем, как с помощью только что рассмотренной операции Teleport можно передать сообщение. Бабушка уже вполне освоилась с квантовой телепортацией и теперь посылает мне не неизвестное квантовое состояние, а известное — сообщение длиной в один бит. Предположим, я спросила бабушку, включила ли она чайник. Ответом будет одно из двух возможных сообщений — да или нет.
Вначале выделим регистр на два кубита, булево сообщение, которое мы будем пересылать (msg), и мой кубит, (there), с помощью которого бабушка будет передавать сообщение. Помните, что нумерация элементов регистра начинается с 0 (так же, как в массивах). Результат выглядит так:
Кубит msg, который мы выделили, изначально находится в состоянии |0〉 (это состояние по умолчанию для всех выделяемых кубитов). Сообщение бабушки о том, включен ли чайник, может принимать одно из двух значений — да или нет. Если ответ — нет, то ничего дополнительно делать не надо — такое сообщение соответствует состоянию |0〉, в котором кубит msg находится изначально. Если ответ — да, то есть |1〉, то нам нужно пропустить кубит msg через квантовый вентиль NOT, чтобы перевести его в показанное ниже состояние.
Далее бабушка передает состояние мне с помощью операции Teleport.
Затем мы измеряем состояние моего кубита, there.
В результате я получаю сообщение объемом 1 бит и узнаю, могу ли я рассчитывать на горячий чай. Так десятки лет исследований в сферах квантовой механики и вычислений нашли очень важное применение.
Если вы запустите код, на экран будут выводиться результаты передачи различных булевых состояний, которые содержатся в файле Driver.cs.
На этом мы закончим.
Это вторая статья из серии о квантовом программировании. Предполагается, что читатель уже знаком с первой частью.
Статьи из цикла:
К сожалению, отправить кубит ни по электронной почте, ни посылкой нельзя. Они передаются по специальным квантовым каналам, а в деревне и Интернет-то появился совсем недавно.
Но, может быть, бабушке удастся передать квантовую информацию по классическому каналу связи (например, через Интернет или телефонную линию)? Проблема заключается в том, что диапазон возможных значений квантового состояния непрерывен, поэтому для его точного описания потребуется бесконечное количество классических бит. Моя бабушка — весьма занятой человек, и у нее нет времени набирать столько бит.
Она уже начала терять всякую надежду, и тут я говорю: «Бабуль, все в порядке». Помнишь, мы в прошлую среду за чаем смастерили состояние Белла? Передать квантовое состояние можно через него! Такая передача квантового состояния с использованием классических каналов связи и называется квантовой телепортацией. Мы постараемся разобраться, как она работает — в теории и в коде.
Отправляем бабушке квантовую почту
Этап 0, подготовительный
Чтобы все описанное ниже сработало, мы с бабушкой должны подготовить состояние Белла: перевести ее кубит |G⟩ и мой кубит |F⟩ в состояние запутанности. Я расстаюсь с бабушкой, но свой кубит (половину состояния Белла) беру с собой. Наши кубиты будут находиться в состоянии запутанности вне зависимости от того, какое расстояние их разделяет — несколько километров или несколько миллиардов световых лет.
Помните, мы обсуждали замечательное свойство запутанных состояний — связанность результатов измерений соответствующих кубитов? Если бабушка измерит состояние своего кубита, это скажется на моем кубите (вне зависимости от расстояния). Ниже мы будем активно использовать это свойство.
Этап 1. Запутывание бабушкиного кубита с |ψ⟩
Исходное состояние будем описывать с помощью приведенной выше диаграммы. В верхнем левом углу находится предмет всех наших стараний — кубит, который бабушка хочет мне отправить. Он находится в неизвестном состоянии, которое можно представить следующим образом:
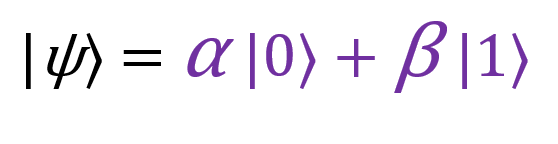
Кроме того, в ее распоряжении находится кубит |G⟩, который, как мы только что обсуждали, запутан с моим кубитом, |F⟩ (эта их связь показана волнистой линией). Теперь два кубита находятся в состоянии Белла, которое описывается формулой
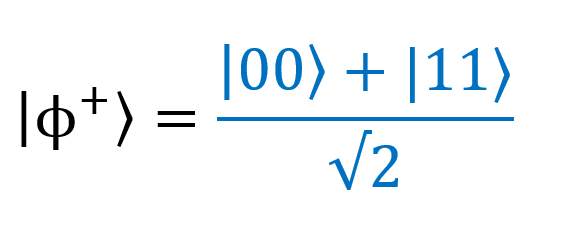
Вначале мы запутаем бабушкин кубит |G⟩ с состоянием |ψ⟩. Скоро поймете зачем. В предыдущей статье мы узнали, что два кубита можно запутать с помощью схемы, состоящей из вентиля CNOT и вентиля Адамара. Давайте посмотрим, как этот процесс представляется с помощью квантовой цепи.
[Чтобы лучше понимать эти обозначения на диаграммах квантовых цепей, рекомендую вкратце ознакомиться со статьей Квантовые цепи и вентили — вводный курс.]
Применение вентиля CNOT
Если добавить вентиль CNOT, схема принимает следующий вид. Состояние, которое подается на вход CNOT, можно записать как |ψ⟩|G⟩, где первый вход соответствует верхнему проводу, второй — среднему. Если подставить определения |ψ⟩ и |G⟩, получим:
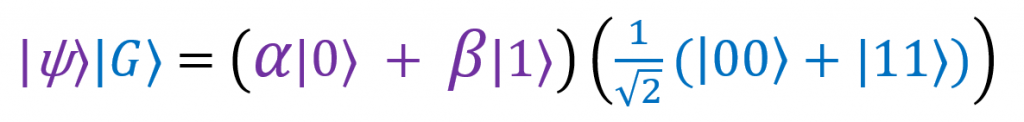
Раскроем скобки:
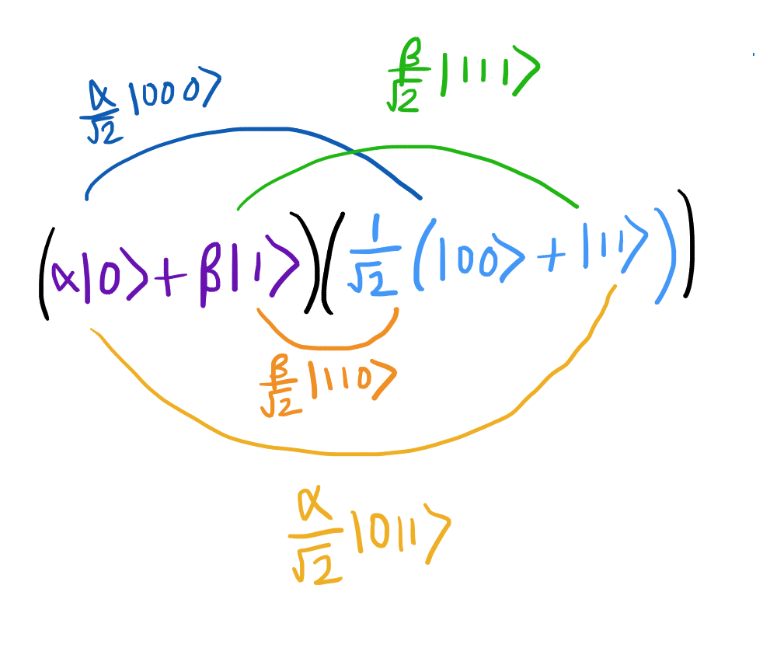
Таким образом, на вход подается
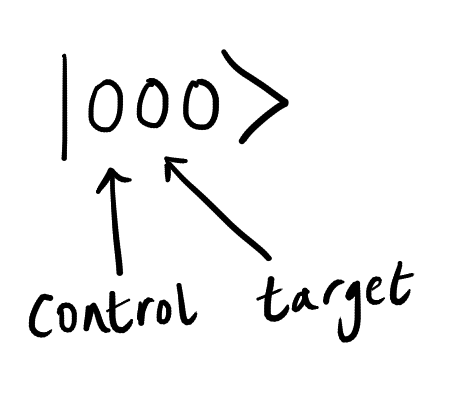
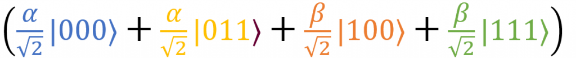. Каждое из этих слагаемых проходит через вентиль CNOT. В первой статье мы видели, как действует вентиль CNOT и как он обрабатывает два кубита. Самые внимательные читатели уже заметили, что все наши слагаемые — |000〉, |011〉, |100〉 и |111〉 — состоят из трех кубитов. В этом случае в роли управляющего кубита используется первый, а управляемым является второй (см. ниже).
Когда управляющий кубит равен |1〉, значение управляемого кубита меняется на противоположное. Таким образом, CNOT превращает набор кубитов |100〉 в |110〉, а |111〉 — в |101〉. Все другие состояния остаются прежними.
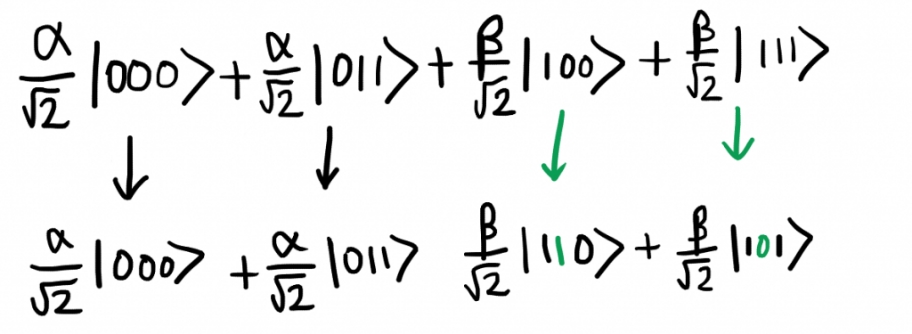
Это значит, что состояние трех кубитов после вентиля CNOT будет описываться следующим выражением:
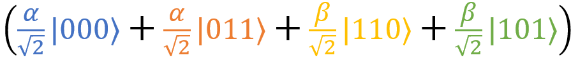.Применение вентиля Адамара
Второй этап запутывания кубита |G⟩ с состоянием |ψ⟩ — применение вентиля Адамара к первому кубиту. Вот как это выглядит на диаграмме квантовой цепи:
Напомню, что вентиль Адамара преобразует |0〉 и |1〉 в состояния
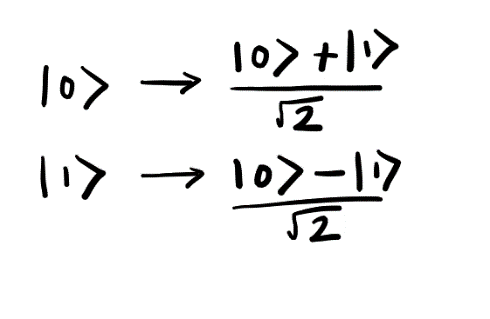
После вентиля CNOT кубиты находились в состоянии
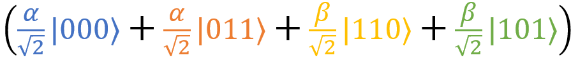. Применим вентиль Адамара к первому кубиту каждого слагаемого. Результат выглядит довольно неаккуратно: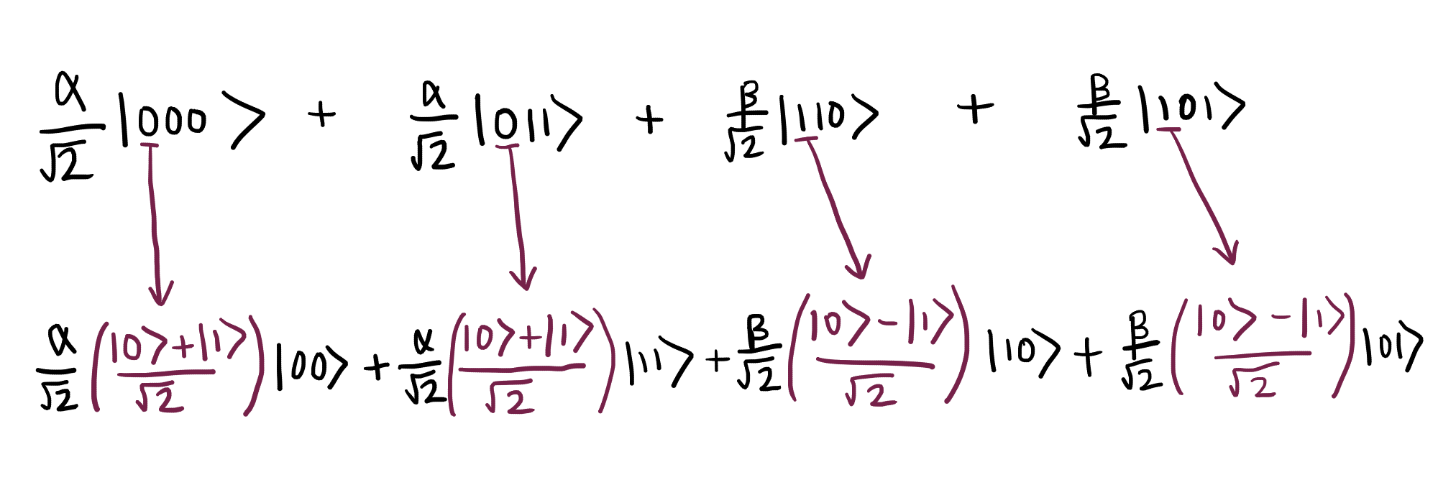
Итак, мы получили
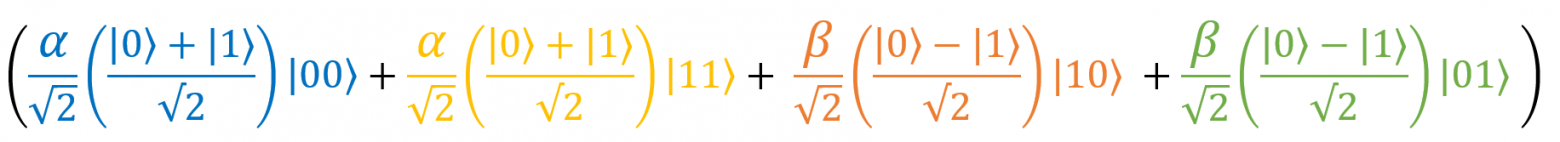
Уберем лишнее
Давайте немного причешем нашу формулу. Как можно заметить, в первом слагаемом
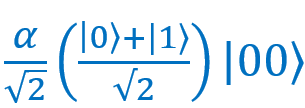есть две дроби со знаменателем √2. Перемножим их: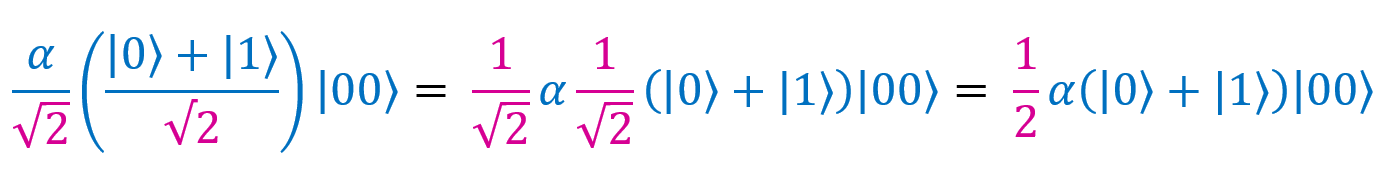
Если применить аналогичную операцию к другим слагаемым, получим
, 
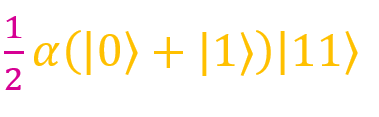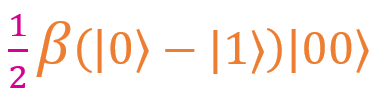и 
. Как можно заметить, у каждой дроби есть множитель 1/2. Если вынести его за скобки, получим: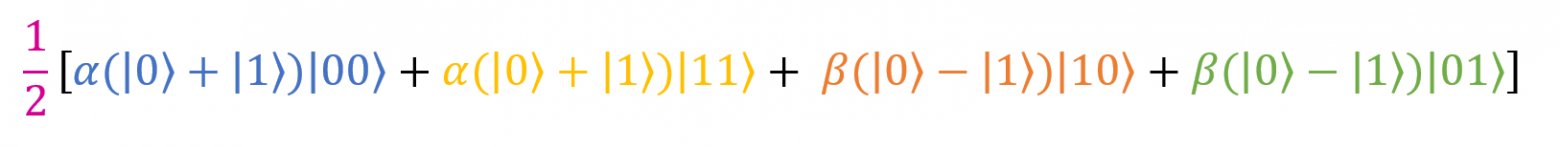 
Выглядит уже лучше. Теперь раскроем скобки (это упростит нам работу на следующем этапе). В качестве примера я приведу выкладки для слагаемого
.
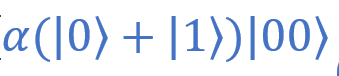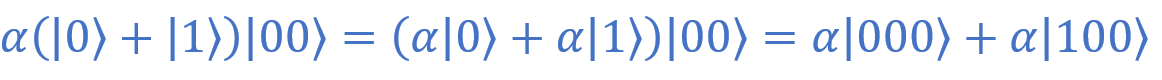
Остальные «читателю предлагается сделать в качестве упражнения». Если честно, я такие заманчивые предложения обычно игнорирую. Вот как будут выглядеть оставшиеся слагаемые, если раскрыть скобки:
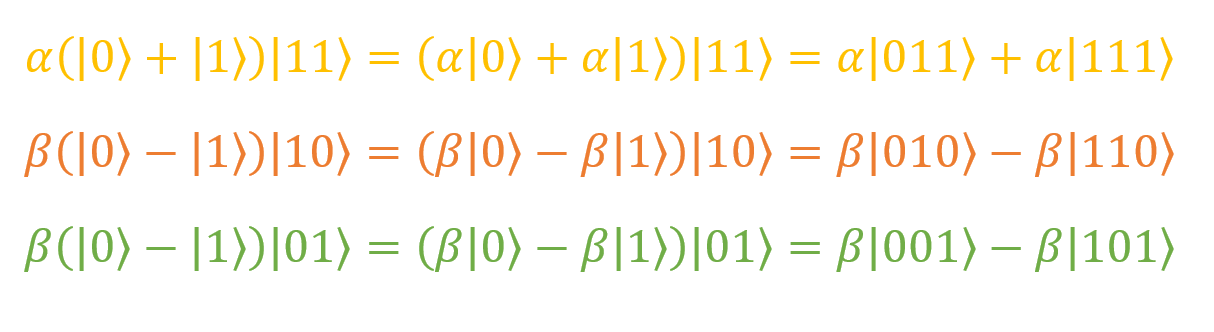
Их сумма равна
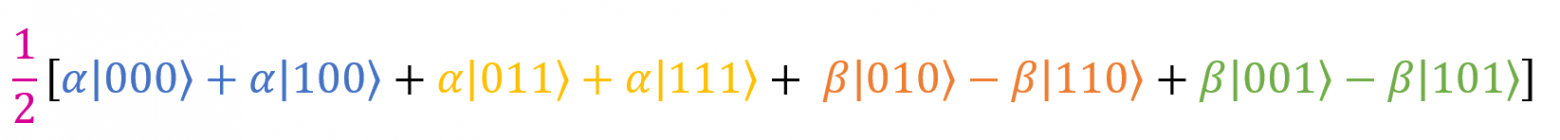
Этап 2. Измерение
Итак, мы запутали бабушкин кубит |G⟩ с кубитом |ψ⟩. Теперь измерим их. Но перед этим результаты нужно привести к виду, более удобному для понимания.
Снова подчищаем результаты
Это последний раз, честное слово. Вот все возможные результаты измерения первого и второго кубита: 00, 01, 10, 11. Пока мы не знаем, каким в каждом из этих случаев будет наш третий кубит. Сгруппируем слагаемые так, чтобы понять, в каком состоянии будет находиться третий кубит, а именно мой кубит |F⟩.
Пока наш результат выглядит так:
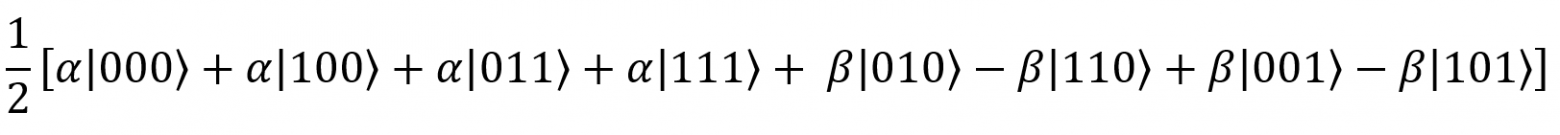
Выделим первый и второй кубит каждого слагаемого:
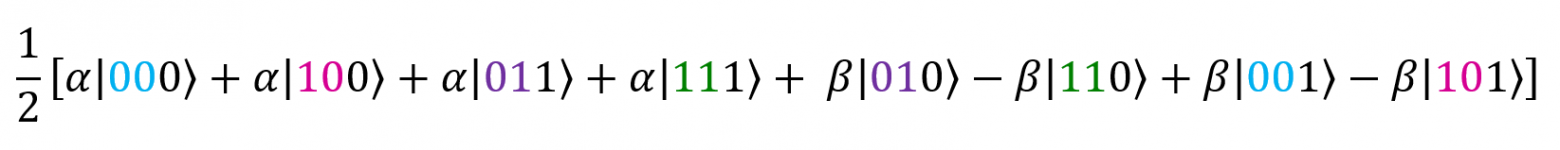
Рассмотрим случаи, в которых первый и второй кубит равны |00〉. Им соответствуют слагаемые
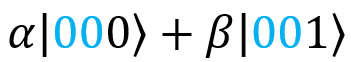. Их можно преобразовать так: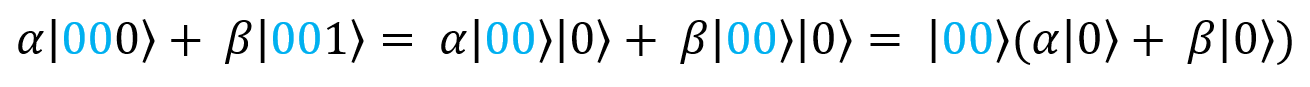 
То же самое можно сделать для случаев |01〉, |10〉 и |11〉.
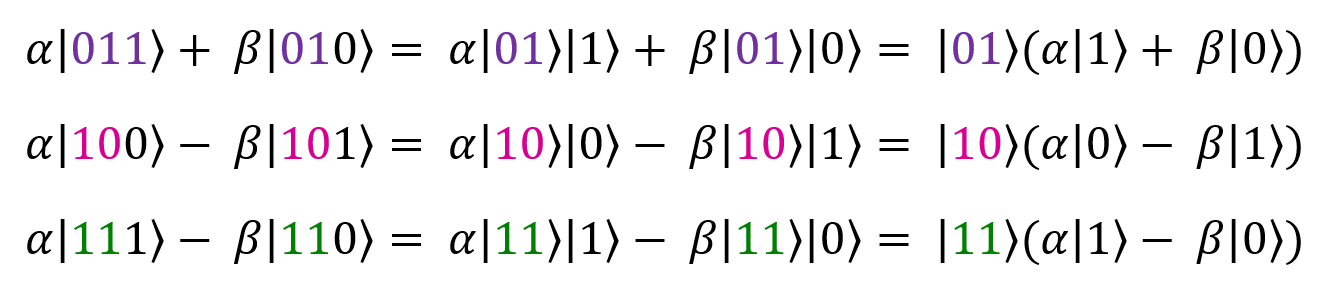
После преобразования выражение принимает следующий вид:
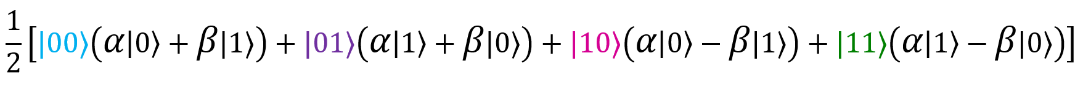
Отлично.
Измерение
Так выглядит наша цепь с добавленными символами измерения. Обратите внимание на двойные черты после символов измерения. Они соответствуют переносу классических битов, которые и являются результатами измерений.
Моя бабушка также измеряет свои два кубита, |G⟩ и |ψ⟩. Как мы уже говорили, всего возможно четыре результата измерения: 00, 01, 10 или 11. При измерении кубита суперпозиция его состояний коллапсирует. Предположим, мы измерили состояние первого кубита |ψ⟩ и получили 0. Суперпозиция коллапсирует, и у нас остаются только те слагаемые, которые согласуются с таким результатом измерения (0), то есть следующие:
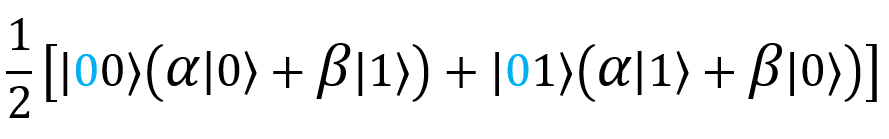
Предположим теперь, что мы измерили состояние второго кубита, |G⟩, и получили 0. Суперпозиция коллапсирует. Остается единственное слагаемое, которое согласуется с обоими результатами измерения (0 и 0), то есть следующее:
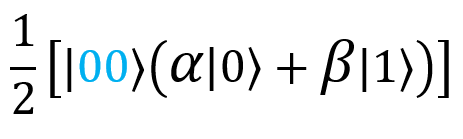
Теперь мы знаем, в каком состоянии находится третий кубит (то есть мой кубит |F⟩): в состоянии
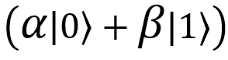.Что, если бы в результате измерения мы получили 01? Вернемся к нашему приведенному результату:
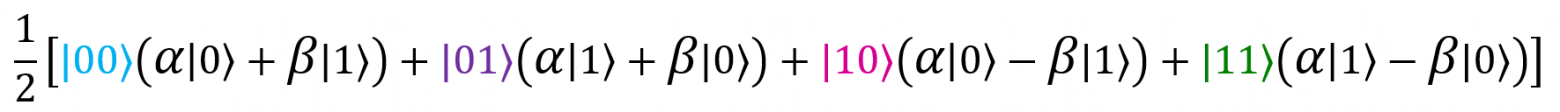
Рассуждая по аналогии, мы поймем, что единственное слагаемое, которое соответствует результату измерения 01 —
, а значит, мой кубит должен находиться в состоянии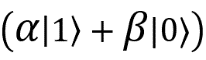 
. Если после измерений бабушка получила результат 10, то я знаю, что третий кубит в состоянии 
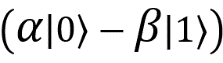, а если она получила 11, то третий кубит равен 
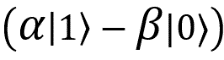.Этот результат можно представить в виде таблицы:
Этап 3. Перевод моего кубита (F) в состояние |ψ⟩
Мы остановились на том, что бабушка измерила состояние своих двух кубитов, позвонила мне и рассказала о результате, так что я знаю состояние моего кубита. Помните, что неизвестное состояние, с которого мы начали, |ψ⟩, было равно
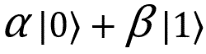. Нам нужно применить к моему кубиту определенные операции, чтобы привести его в это состояние — в состояние, которое мне хотела отправить бабушка (в противном случае я получу нечто совсем иное).Сейчас сделать это будет просто. Взгляните на таблицу выше. Если результат измерений 00, а мой кубит находится в состоянии
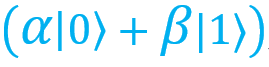, то выполнять какие-либо операции над ним не нужно — он уже в состоянии |ψ⟩. Это самый простой случай.Если результат измерений 01, то мой кубит находится в состоянии
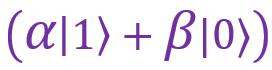. Если сравнить его с состоянием |ψ⟩, станет понятно, что нам нужно поменять местами коэффициенты при |0〉 и |1〉. Для этого просто пропустим мой кубит через вентиль NOT, то есть вентиль X, и получим нужный результат 
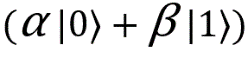.При результате измерений 10 мой кубит находится в состоянии
. Сравним его с |ψ⟩. У нас есть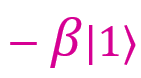 
, а нужно 
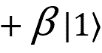. Чтобы сделать желаемое действительным, применим вентиль Z, который меняет знак.И последний вариант — 11. В этом случае мой кубит находится в состоянии
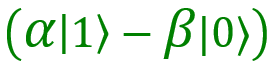. Здесь нужно поменять местами коэффициенты при |0〉 и 1〉, а также знак при 
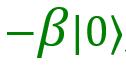. Таким образом, мой кубит нужно пропустить через вентиль X, а потом через Z. Тогда мы получим нужный результат, 
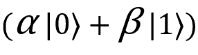. Внесем эти операции в таблицу.
Обратите внимание: если первый бит результата измерения равен 1, то мы применяем вентиль Z, а если второй бит равен 1, то применяем вентиль X. Окончательный вариант цепи показан ниже. Мы добавили вентиль Z, используя верхний провод в качестве управляющего, и вентиль X, для которого управляющим будет второй провод. Управляемым при этом будет мой кубит (потому что именно его нужно обработать с помощью вентилей).
Итак, мы показали, что бабушке достаточно передать всего два классических бита (а именно результаты измерения состояний кубитов |G⟩ и |ψ⟩), чтобы мы могли узнать неизвестное до этого состояние кубита. Благодаря явлению квантового запутывания информация от бабушки помогает узнать значения коэффициентов α и β. При этом нам удалось обойтись без канала квантовой связи. Поэтому такой метод называется квантовой телепортацией.
Подготавливаем и запускаем код
Итак, мы немного разобрались в теории квантовой телепортации. Пора переходить к коду!
Если на каком-либо шаге вам понадобится помощь, готовый код доступен здесь (просто клонируйте или скачайте репозиторий, откройте файл QuantumTeleportation.sln в Visual Studio и переходите к этапу 5).
Этап 1. Создайте проект
Создайте в Visual Studio новый проект типа «Приложение Q#» и присвойте ему какое-нибудь простое и понятное название — например, QuantumTeleportation.
Этап 2. Загрузите копию кода
Загрузите копию кода с примерами квантовых вычислений на свой компьютер. Для этого клонируйте или скачайте репозиторий.
Этап 3. Измените файл Operation.qs
Теперь нужно заменить весь код в файле Operation.qs на код из файла TeleportationSample.qs, который находится в разделе Quantum > Samples > Teleportation здесь.
Этап 4. Измените файл Driver.cs
Замените весь код в файле Driver.cs на содержимое файла Program.cs.
Этап 5. Сохраните и запустите проект
Нажмите на кнопку «start», чтобы запустить код. На экран будут выведены результаты для итераций 0–8. Они должны выглядеть примерно так:
Разбираемся, как этот код работает
На самом деле вы сможете в нем разобраться и без моей помощи — код замечательно прокомментирован. Мы просто сопоставим его с теорией, разобранной выше, — это будет несложно.
Этап 1. Телепортация
В первой части статьи мы говорили о трех кубитах: кубит в неизвестном состоянии |ψ⟩ и два кубита в состоянии Белла (один у бабушки, второй у меня). Этим трем кубитам в операции Teleport (Телепортация) соответствуют кубиты msg (неизвестное состояние, которое мне отправляет бабушка), here (кубит у бабушки) и there (мой кубит F, где |ψ⟩ — пересылаемое состояние).
Как уже обсуждалось, мы с бабушкой заранее подготовили пару кубитов в состоянии Белла. Один из них находится у бабушки, второй — у меня. Поэтому в самом начале нам нужно запутать ее кубит, который называется here, с моим, there. В коде для этого используются вентиль Адамара и вентиль CNOT:
Воспользуемся нашей диаграммой цепи. Я буду добавлять на нее обозначения по мере их появления в коде.
Повторяя операции, описанные в начале статьи, мы запутываем кубит бабушки here с неизвестным квантовым состоянием msg. Вентиль CNOT и вентиль Адамара на диаграмме соответствуют следующим строкам кода:
Затем мы измерили первый и второй кубиты, msg и here. О результатах именно этих измерений бабушка сообщила мне по телефону. Этим событиям соответствуют условия оператора if:
Как мы обсуждали в конце первой части этой публикации, после получения результатов измерения нужно изменить состояние моего кубита так, чтобы оно соответствовало кубиту |ψ⟩, то есть msg. Как мы говорили, если результат измерения первого кубита равен 1, то мой кубит (there) нужно пропустить через вентиль Z. Эта операция показана выше. Если результат измерения второго кубита равен 1, то мой кубит нужно пропустить через вентиль X.
Готово! Теперь мой кубит находится именно в том состоянии, которое мне хотела передать бабушка.
Этап 2. TeleportClassicalMessage
Давайте подумаем, как с помощью только что рассмотренной операции Teleport можно передать сообщение. Бабушка уже вполне освоилась с квантовой телепортацией и теперь посылает мне не неизвестное квантовое состояние, а известное — сообщение длиной в один бит. Предположим, я спросила бабушку, включила ли она чайник. Ответом будет одно из двух возможных сообщений — да или нет.
Вначале выделим регистр на два кубита, булево сообщение, которое мы будем пересылать (msg), и мой кубит, (there), с помощью которого бабушка будет передавать сообщение. Помните, что нумерация элементов регистра начинается с 0 (так же, как в массивах). Результат выглядит так:
Кубит msg, который мы выделили, изначально находится в состоянии |0〉 (это состояние по умолчанию для всех выделяемых кубитов). Сообщение бабушки о том, включен ли чайник, может принимать одно из двух значений — да или нет. Если ответ — нет, то ничего дополнительно делать не надо — такое сообщение соответствует состоянию |0〉, в котором кубит msg находится изначально. Если ответ — да, то есть |1〉, то нам нужно пропустить кубит msg через квантовый вентиль NOT, чтобы перевести его в показанное ниже состояние.
Далее бабушка передает состояние мне с помощью операции Teleport.
Затем мы измеряем состояние моего кубита, there.
В результате я получаю сообщение объемом 1 бит и узнаю, могу ли я рассчитывать на горячий чай. Так десятки лет исследований в сферах квантовой механики и вычислений нашли очень важное применение.
Если вы запустите код, на экран будут выводиться результаты передачи различных булевых состояний, которые содержатся в файле Driver.cs.
На этом мы закончим.
Ресурсы
- Более подробная информация доступна на веб-сайте Microsoft Quantum
- Загрузите Quantum Development Kit
- Подпишитесь на информационный бюллетень Microsoft Quantum
- Узнавайте о новейших разработках из блога Microsoft Quantum
