Принято считать, что две базовые операции «машинного обучения» — это регрессия и классификация. Регрессия — это не только инструмент для выявления параметров зависимости y(x) между рядами данных x и y (чему я уже посвятил несколько статей), но и частный случай техники их сглаживания. В этом примере мы пойдем чуть дальше и рассмотрим, как можно проводить сглаживание, когда вид зависимости y(x) заранее неизвестен, а также, как можно отфильтровать данные, которые контролируются разными эффектами с существенно разными временными характеристиками.
Один из самых популярных алгоритмов сглаживания, применяемый, в частности, в биржевой торговле — это скользящее усреднение (включаю его в цикл статей по машинному обучению с некоторой натяжкой). Рассмотрим скользящее усреднение на примере колебаний курса доллара на протяжении нескольких последних недель (опять-таки в качестве инструмента исследования используя Mathcad). Сами расчеты лежат здесь.
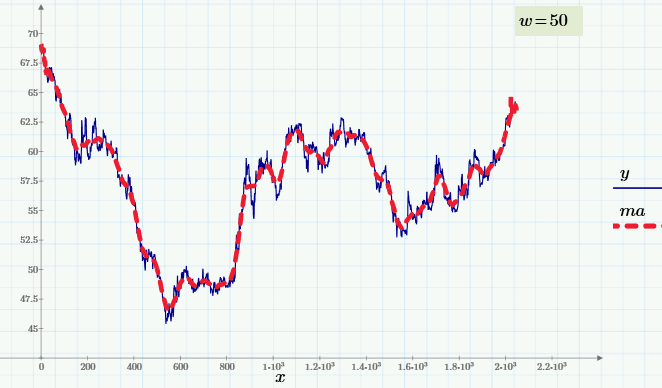
Приведенный график демонстрирует биржевое значение курса доллара к рублю с интервалом в 1 час. Исходные данные представлены синей кривой, а сглаженные — красной. Даже невооруженным глазом видно, что колебания курса имеют несколько характерных частот, что и является предметом одного из направлений технического анализа рынков.
Сглаживание при помощи «скользящего среднего»
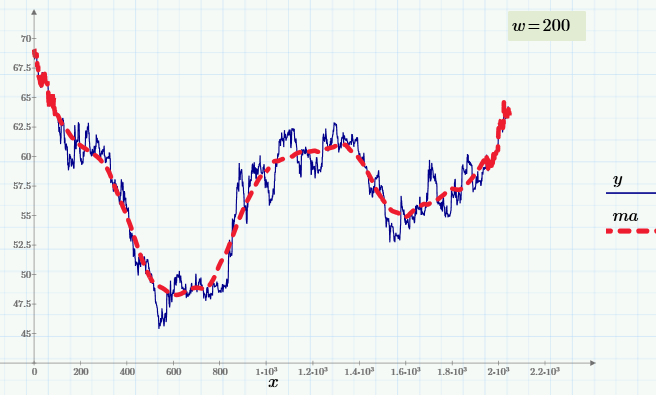
Принцип сглаживания на основе «скользящего среднего» (МА — от англ. «moving average») состоит в расчете для каждого значения аргумента yi среднего значения по соседним w данным.
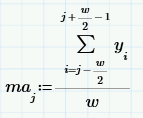
Число w называют окном скользящего усреднения: чем оно больше, тем больше данных участвуют в расчете среднего, соответственно, тем более гладкая кривая получается. На верхнем рисунке окно w=50, а вот как будет выглядеть скользящее усреднение при w=200.
Как меняется Фурье-спектр данных при скользящем усреднении?
Очевидно, что при малых w сглаженные кривые практически повторяют ход изменения данных, а при больших w — отражают лишь закономерность их медленных вариаций. Это типичный пример фильтрации данных, т.е. устранения одной из составляющих зависимости y(xi). Наиболее часто целью фильтрации является подавление быстрых вариаций y(xi), которые обычно обусловлены шумом. В результате из быстроосциллирующей зависимости y(xi) получается другая, сглаженная зависимость, в которой доминирует более низкочастотная составляющая.
Эти рассуждения плавно перевели нас к терминологии спектров. Давайте нарисуем график Фурье-преобразования («Фурье-спектр») исходных данных:
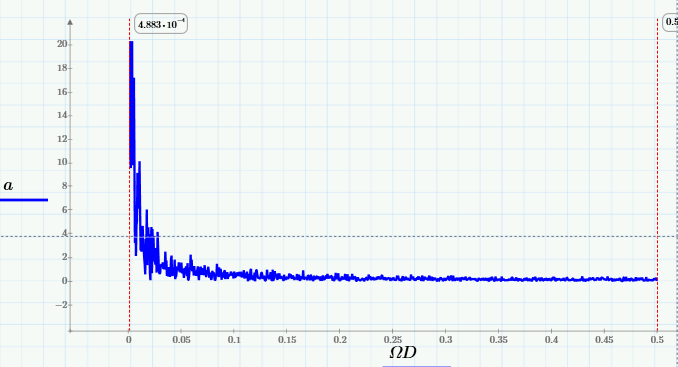
и убедимся в том, что спектр скользящего среднего вырезает из него высокие частоты (начиная примерно с частоты 0.005 Гц):
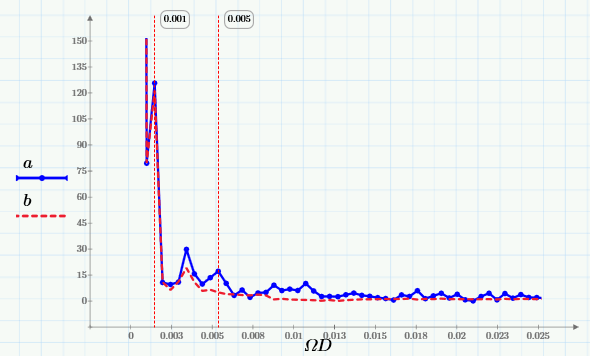
Пояснение: Фурье-спектр суммы синусов и ее МА
Для того чтобы пояснить принцип расчета Фурье-спектра, рассмотрим вместо (случайных) исходных данных простую модель суммы нескольких детерминированных сигналов (синусоид с разной частотой и амплитудой) и псевдослучайного шума:
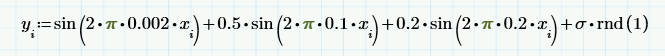
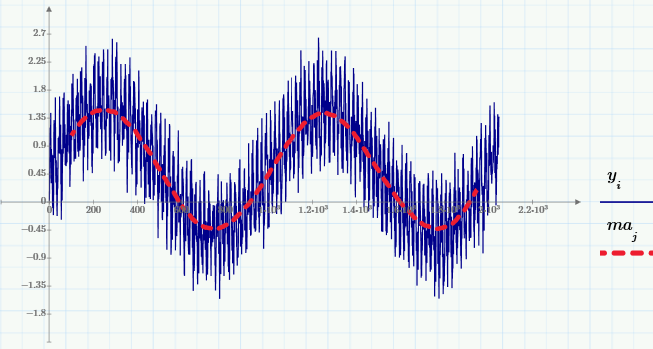
Приведем графики этой суммы и ее МА (с тем же окном w=200):
а также их Фурье-спектры:
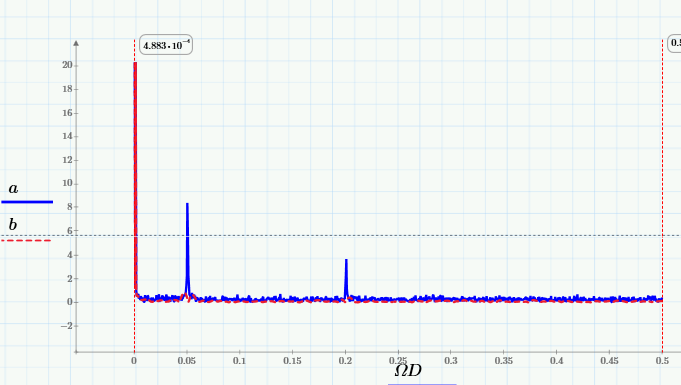
Из них видно, что скользящее усреднение вырезает из сигнала высокие частоты, начиная с частоты 0.005 Гц. Лучше это видно на крупном плане низкочастотной области спектра:
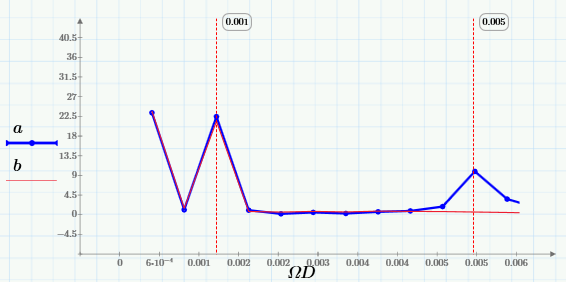
Таким образом, выбирая подходящее окно, можно сдвигать область подавляемых частот в нужную сторону (чем больше w, тем дальше эта граница сдвигается влево).
Полосовая фильтрация
Вернемся к биржевой аналитике и продемонстрируем исключительно простой способ вырезания из исходных данных нужной полосы частот. А именно, в противоположность подавления шума (высокочастотной составляющей) часто рассматривают и противоположную задачу — устранение медленно меняющихся вариаций (иногда эту задачу называют устранением тренда, или детрендингом). При помощи скользящего усреднения ее реализовать очень просто — путем вычитания из сигнала МА (с подобранным окном):
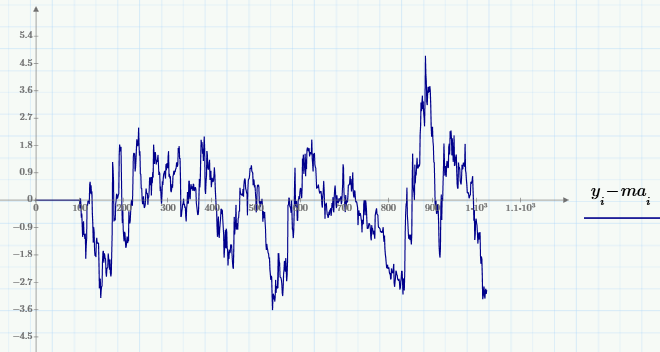
Также интерес представляют смешанные задачи выделения среднемасштабных вариаций путем подавления как более быстрых, так и более медленных вариаций. Одна из возможностей решения связана с применением «полосовой фильтрации», которая реализуется так:
1. Устранение из сигнала y высокочастотной составляющей, имеющее целью получить сглаженный сигнал middle, например, с помощью скользящего усреднения с малым окном (например, w=200).
2. Выделение из сигнала middle низкочастотной составляющей slow, например, путем скользящего усреднения с большим окном w.
3. Вычитание из сигнала middle тренд slow, тем самым выделяя среднемасштабную составляющую исходного сигнала y.
Оставляю заинтересовавшемуся читателю возможность самому реализовать полосовую фильтрацию в Mathcad Express (с небольшой оговоркой, что в бесплатной версии Маткада алгоритм БПФ расчета Фурье-спектров отключен, и с ним поиграться не получится). Сами расчеты находятся здесь.
Литература:
1. Кирьянов Д.В., Кирьянова Е.Н. Вычислительная физика (PDF, гл.1, п.6 и 7). М.: Полибук Мультимедиа, 2006.
2. Бат М. Спектральный анализ в геофизике. М., Наука, 1980.
Один из самых популярных алгоритмов сглаживания, применяемый, в частности, в биржевой торговле — это скользящее усреднение (включаю его в цикл статей по машинному обучению с некоторой натяжкой). Рассмотрим скользящее усреднение на примере колебаний курса доллара на протяжении нескольких последних недель (опять-таки в качестве инструмента исследования используя Mathcad). Сами расчеты лежат здесь.

Приведенный график демонстрирует биржевое значение курса доллара к рублю с интервалом в 1 час. Исходные данные представлены синей кривой, а сглаженные — красной. Даже невооруженным глазом видно, что колебания курса имеют несколько характерных частот, что и является предметом одного из направлений технического анализа рынков.
Сглаживание при помощи «скользящего среднего»
Принцип сглаживания на основе «скользящего среднего» (МА — от англ. «moving average») состоит в расчете для каждого значения аргумента yi среднего значения по соседним w данным.
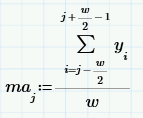
Число w называют окном скользящего усреднения: чем оно больше, тем больше данных участвуют в расчете среднего, соответственно, тем более гладкая кривая получается. На верхнем рисунке окно w=50, а вот как будет выглядеть скользящее усреднение при w=200.

Как меняется Фурье-спектр данных при скользящем усреднении?
Очевидно, что при малых w сглаженные кривые практически повторяют ход изменения данных, а при больших w — отражают лишь закономерность их медленных вариаций. Это типичный пример фильтрации данных, т.е. устранения одной из составляющих зависимости y(xi). Наиболее часто целью фильтрации является подавление быстрых вариаций y(xi), которые обычно обусловлены шумом. В результате из быстроосциллирующей зависимости y(xi) получается другая, сглаженная зависимость, в которой доминирует более низкочастотная составляющая.
Эти рассуждения плавно перевели нас к терминологии спектров. Давайте нарисуем график Фурье-преобразования («Фурье-спектр») исходных данных:

и убедимся в том, что спектр скользящего среднего вырезает из него высокие частоты (начиная примерно с частоты 0.005 Гц):

Пояснение: Фурье-спектр суммы синусов и ее МА
Для того чтобы пояснить принцип расчета Фурье-спектра, рассмотрим вместо (случайных) исходных данных простую модель суммы нескольких детерминированных сигналов (синусоид с разной частотой и амплитудой) и псевдослучайного шума:
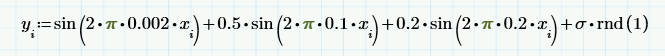
Приведем графики этой суммы и ее МА (с тем же окном w=200):

а также их Фурье-спектры:

Из них видно, что скользящее усреднение вырезает из сигнала высокие частоты, начиная с частоты 0.005 Гц. Лучше это видно на крупном плане низкочастотной области спектра:

Таким образом, выбирая подходящее окно, можно сдвигать область подавляемых частот в нужную сторону (чем больше w, тем дальше эта граница сдвигается влево).
Полосовая фильтрация
Вернемся к биржевой аналитике и продемонстрируем исключительно простой способ вырезания из исходных данных нужной полосы частот. А именно, в противоположность подавления шума (высокочастотной составляющей) часто рассматривают и противоположную задачу — устранение медленно меняющихся вариаций (иногда эту задачу называют устранением тренда, или детрендингом). При помощи скользящего усреднения ее реализовать очень просто — путем вычитания из сигнала МА (с подобранным окном):

Также интерес представляют смешанные задачи выделения среднемасштабных вариаций путем подавления как более быстрых, так и более медленных вариаций. Одна из возможностей решения связана с применением «полосовой фильтрации», которая реализуется так:
1. Устранение из сигнала y высокочастотной составляющей, имеющее целью получить сглаженный сигнал middle, например, с помощью скользящего усреднения с малым окном (например, w=200).
2. Выделение из сигнала middle низкочастотной составляющей slow, например, путем скользящего усреднения с большим окном w.
3. Вычитание из сигнала middle тренд slow, тем самым выделяя среднемасштабную составляющую исходного сигнала y.
Оставляю заинтересовавшемуся читателю возможность самому реализовать полосовую фильтрацию в Mathcad Express (с небольшой оговоркой, что в бесплатной версии Маткада алгоритм БПФ расчета Фурье-спектров отключен, и с ним поиграться не получится). Сами расчеты находятся здесь.
Литература:
1. Кирьянов Д.В., Кирьянова Е.Н. Вычислительная физика (PDF, гл.1, п.6 и 7). М.: Полибук Мультимедиа, 2006.
2. Бат М. Спектральный анализ в геофизике. М., Наука, 1980.