Собеседования по алгоритмам: максимальная конкатенация
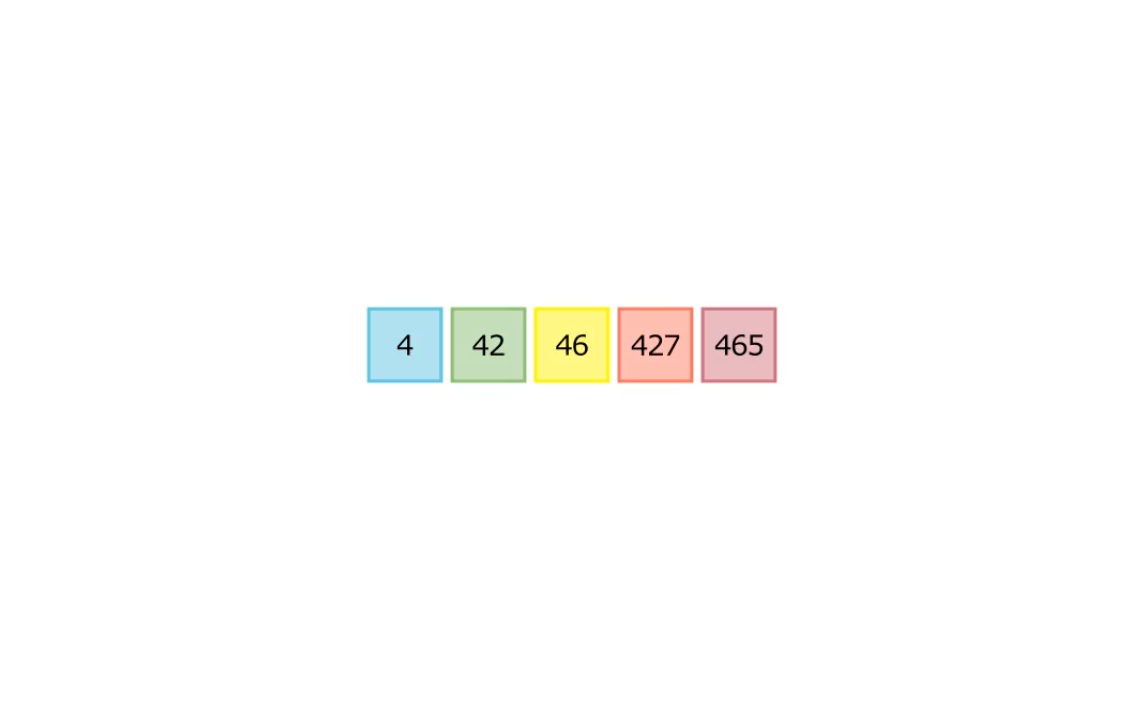
Чему равно самое большое число, которое можно составить из этих пяти карточек? И как написать программу, которая быстро найдёт ответ, получив на вход сто таких карточек?
Исследователь, автор курсов по алгоритмам

Чему равно самое большое число, которое можно составить из этих пяти карточек? И как написать программу, которая быстро найдёт ответ, получив на вход сто таких карточек?
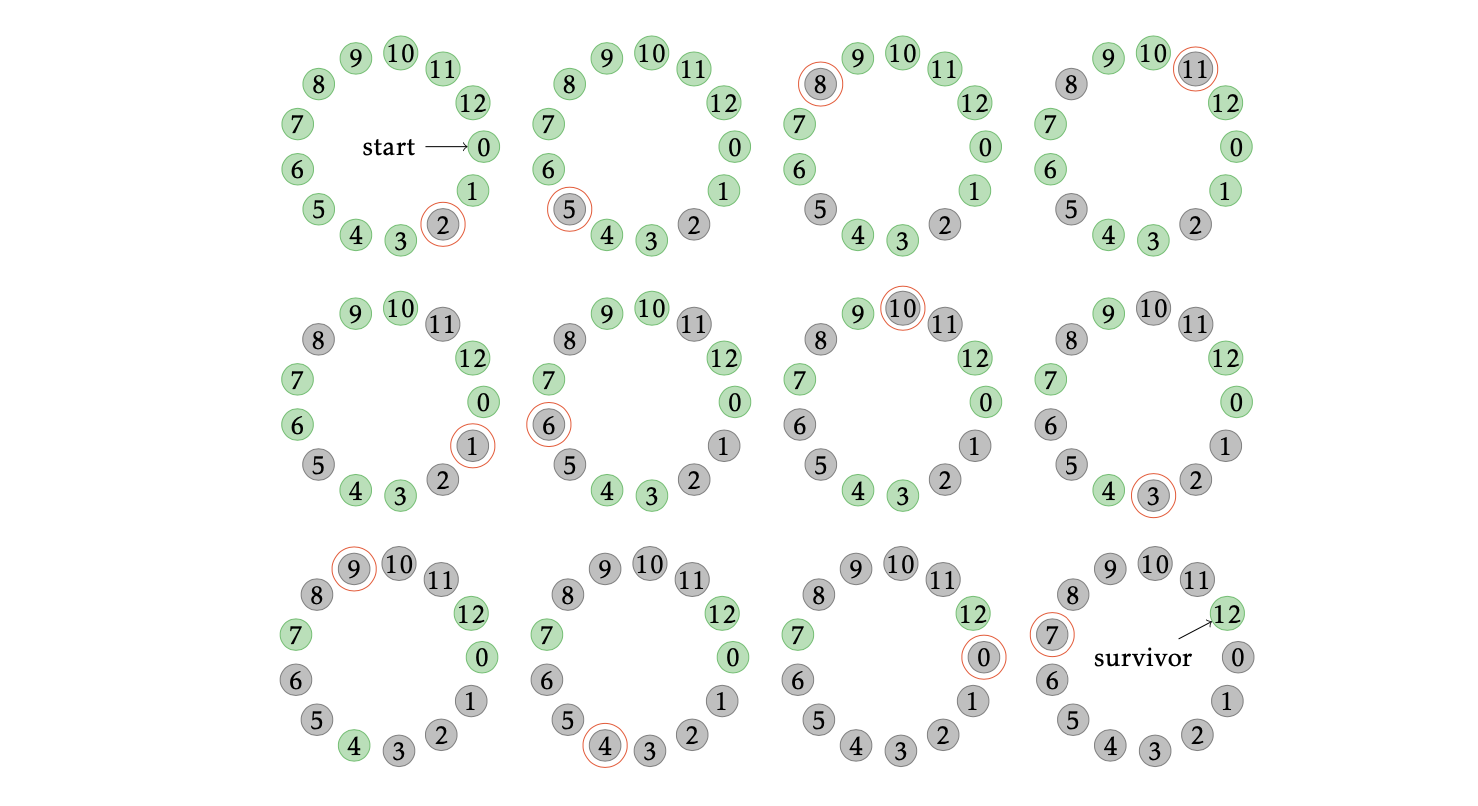
На следующем собеседовании по алгоритмам вам может попасться алгоритмическая задача, основанная на легенде об Иосифе Флавии: стоящие по кругу n мятежников начинают убивать каждого k-го из оставшихся в живых; нужно написать программу, которая получает на вход числа n и k и за время O(n) находит номер последнего оставшегося в живых мятежника. Сможете написать такую программу за тридцать минут? В этой статье мы подробно разберём решение задачи.

Собеседования в крупные IT-компании почти всегда содержат алгоритмическую секцию — даже если вы собеседуетесь на позицию, в работе на которой алгоритмы возникать вряд ли будут. Ниже мы приводим пример задачи, с которой вы можете столкнуться на вашем следующем интервью. Мы расскажем, как эта задача решается, но мы настоятельно рекомендуем вам читать решение только после того, как вы попробуете решить задачу самостоятельно: во-первых, это отличная тренировка; во-вторых, вы лучше запомните решение, если придумаете его сами (не отказывайте себе в этом удовольствии!); в-третьих, даже если вы подумаете над задачей, но не решите её, время не будет потеряно: прочитав потом решение, вы лучше его поймёте и оцените его красоту.




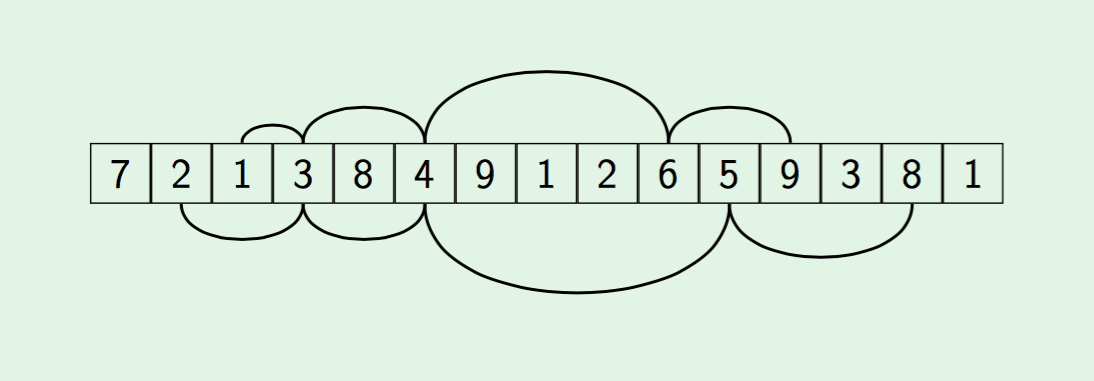

Задача 1. Дан массив A длины (n+1), содержащий натуральные числа от 1 до n. Найти любой повторяющийся элемент за время O(n), не изменяя массив и не используя дополнительной памяти.
Задача 2. Дана матрица nxn, содержащая попарно различные натуральные числа. Требуется найти в ней локальный минимум за время O(n).

 |
Константин Макарычев (Microsoft Research) Молодой, но уже очень успешный учёный. Специалист по приближённым алгоритмам и Unique games conjecture (гипотезе, из которой выводятся результаты о неприближаемости для многих NP-трудных задач). |
 |
Александр Шень (Montpellier Laboratory of Informatics, Robotics, and Microelectronics и ИППИ РАН) Наверное, не нуждается в представлении. Специалист в области теории сложности.Автор многих замечательных учебников — таких, например, как «Программирование: теоремы и задачи». Также является редактором перевода (и, на самом деле, главным переводчиком) первого издания классического учебника Кормена, Лейзерсона, Ривеста «Алгоритмы: построение и анализ». |
 |
Mario Szegedy (Rutgers University) Дважды лауреат Премии Гёделя, присуждающейся ежегодно за выдающиеся статьи в области theoretical computer science. Первый раз — за вклад в доказательство PCP-теоремы (вероятностно проверяемых доказательств) и её применение к результатам о неприближаемости, второй — за работы в области streaming algorithms. |
 |
Ryan Williams (Stanford University) Тоже молодая звезда. Его недавний результат о том, что класс NEXP не содержится в классе ACC0, называют одним из самых значительных достижений в области схемной сложности за последние 20 лет. И это далеко не единственный его результат. Ещё, например, он показал, как найти максимальный разрез в графе быстрее полного перебора с неожиданным и элегантным использованием быстрого умножения матриц. |
 теперь умеют умножать за
теперь умеют умножать за 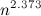 . Другими словами, доказано, что
. Другими словами, доказано, что 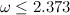 , где
, где 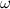 — экспонента умножения матриц. Доказала это совсем недавно Вирджиния Василевска-Вильямс, улучшив тем самым оценку
— экспонента умножения матриц. Доказала это совсем недавно Вирджиния Василевска-Вильямс, улучшив тем самым оценку 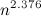 , полученную Копперсмитом и Виноградом в 1987 году. Я напишу про важность этого алгоритма совсем немножко. Тем, кому интересно узнать побольше, предлагается почитать посты Скотта Ааронсона, Ричарда Липтона и Билла Гасарша.
, полученную Копперсмитом и Виноградом в 1987 году. Я напишу про важность этого алгоритма совсем немножко. Тем, кому интересно узнать побольше, предлагается почитать посты Скотта Ааронсона, Ричарда Липтона и Билла Гасарша.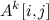 — количество (не обязательно простых!) путей длины k между вершинами i и j. Эта простая идея позволяет за время
— количество (не обязательно простых!) путей длины k между вершинами i и j. Эта простая идея позволяет за время 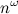 проверить, есть ли в графе треугольник (3-клика): нужно возвести матрицу смежности в куб (для этого потребуется два умножения матриц) и посмотреть на диагональ. Отметим, что речь здесь именно о теоретических оценках, поскольку продвинутые алгоритмы умножения матриц хоть и обгоняют асимптотически простой кубический алгоритм, но на практике дают ускорение только на огромных размерах матриц.
проверить, есть ли в графе треугольник (3-клика): нужно возвести матрицу смежности в куб (для этого потребуется два умножения матриц) и посмотреть на диагональ. Отметим, что речь здесь именно о теоретических оценках, поскольку продвинутые алгоритмы умножения матриц хоть и обгоняют асимптотически простой кубический алгоритм, но на практике дают ускорение только на огромных размерах матриц.
