
Поднявшаяся в этом топике дискуссия о криптостойкости многократного применения хеша над паролем (проскальзывавшая, кстати, и в других форумах), подтолкнула меня к этому немного математическому топику. Суть проблемы возникает из идеи многократной (1.000 и более раз) обработки пароля перед хранением каким-либо криптостойким алгоритмом (чаще всего хеш-функцией) с целью получить медленный алгоритм проверки, тем самым эффективно противостоящий brute force-у в случае перехвата или кражи злоумышленником этого значения. Как совершенно верно отметили хабрапользователи Scratch (автор первой статьи), mrThe и IlyaPodkopaev, идея не нова и ею пользуются разработчики оборудования Cisco, архиватора RAR и многие другие. Но, поскольку хеширование – операция сжимающая множество значений, возникает вполне закономерный вопрос – а не навредим ли мы стойкости системы? Попытка дать ответ на этот вопрос –
Снижение стойкости будем рассматривать в двух моделях угроз:
- перебор злоумышленником случайных входных наборов байт в надежде найти коллизию из-за сужения пространства значений («полный перебор»);
- перебор по словарю.
Начнем с первого, более теоретического, вопроса: «сможет ли такое огромное пространство значений современной хеш-функции 2128 (MD5), 2160 (SHA-1), 2256 (ГОСТ Р 34.11, SHA-256) в результате многократного применения сузиться до такой степени, что коллизию к нему можно будет подобрать простым случайным поиском ?».
Начало
Одним из основных свойств/требований к криптостойким хеш-функциям является очень хорошая равномерность распределения выходных результатов. Это позволяет оперировать в потребующихся далее оценках обычной теорией вероятности и комбинаторикой.
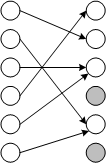
Возьмем входное множество из N элементов и каждому из его объектов сопоставим в выходном множестве также из N объектов случайным образом какой-либо элемент (см. рис.). Очевидно, что несколько отображений покажут на одинаковые элементы, а, следовательно, останутся и элементы, к которым не подходит ни одной стрелки:
Вероятность того, что конкретный элемент выходного множества НЕ будет выбран конкретным отображением (стрелкой) равна
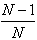 , соответственно, вероятность того, что он НЕ будет выбран ни одной из N стрелок равна
, соответственно, вероятность того, что он НЕ будет выбран ни одной из N стрелок равна  или что тоже самое
или что тоже самое  (благодаря свойству криптостойкой хеш-функции все N отображений – события независимые в первом приближении).
(благодаря свойству криптостойкой хеш-функции все N отображений – события независимые в первом приближении).Предел
 является следствием второго замечательного предела и равен
является следствием второго замечательного предела и равен  , т.е. примерно 0,3679. Это вероятность того, что элемент в выходном множестве «станет серым». Попутно отметим, что при больших N (больше 232) степень «ухудшения» не зависит от разрядности хеш-функции. В итоге после первого повтора хеширования от пространства значений останется только около 63%. Если дальше всё пойдет также, то это будет катастрофой – всего за 150 итераций мы «съедим» 100 бит выходного пространства, оставив, например, для MD5 только 2128-100=228 вариантов. К счастью, это не так.
, т.е. примерно 0,3679. Это вероятность того, что элемент в выходном множестве «станет серым». Попутно отметим, что при больших N (больше 232) степень «ухудшения» не зависит от разрядности хеш-функции. В итоге после первого повтора хеширования от пространства значений останется только около 63%. Если дальше всё пойдет также, то это будет катастрофой – всего за 150 итераций мы «съедим» 100 бит выходного пространства, оставив, например, для MD5 только 2128-100=228 вариантов. К счастью, это не так.Детально
Как только входное множество начинает быть заполненным не полностью (т.е. после второй итерации в первой модели угроз или сразу же во второй модели угроз (с атакой по словарю)), начинают работать другие формулы и другие закономерности. Это хорошо видно на том же рисунке для случая, если во входном множестве было всего 3 «активных» элемента. Вероятность «потерять» элемент (сузить выходное множество) резко уменьшается, т.к. теперь гораздо реже два и более отображения встречаются на одном и том же элементе.

Пусть во входном множестве было активно только kN элементов, где 0<k<1. Тогда вероятность НЕ выбора конкретного элемента равна
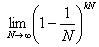 , что по тому же следствию равно
, что по тому же следствию равно  , а сужение выходного множества на этой итерации составит всего
, а сужение выходного множества на этой итерации составит всего  . Вот таблица первых 6 итераций:
. Вот таблица первых 6 итераций:| Номер итерации, i | Доля множества значений, k |
|---|---|
| 1 | 1,0000 |
| 2 | 0,6321 |
| 3 | 0,4685 |
| 4 | 0,3740 |
| 5 | 0,3120 |
| 6 | 0,2680 |
Конечно, доля активных элементов продолжает с каждой итерацией уменьшаться, но не так быстро и катастрофично как в самом начале.
Для того чтобы оценить степень снижения стойкости для большого количества итераций удобнее изучать не само число k, а обратное ему – во сколько раз сократилось выходное множество, причем сразу в логарифмической шкале по основанию 2, чтобы единицами измерения стали биты:
 . Именно это число будет характеризовать снижение стойкости к полному перебору – его необходимо вычесть из разрядности выбранной хеш-функции, чтобы получить разрядность эквивалентно стойкой хеш-функции. График зависимости r до 50.000 итераций приведен на рисунке:
. Именно это число будет характеризовать снижение стойкости к полному перебору – его необходимо вычесть из разрядности выбранной хеш-функции, чтобы получить разрядность эквивалентно стойкой хеш-функции. График зависимости r до 50.000 итераций приведен на рисунке: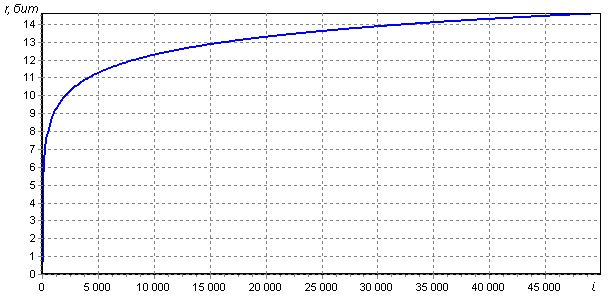
Точки, в которых график пересекает целые значения r, сведены в таблицу:
| Снижение стойкости, r (бит) | Кол-во итераций, i |
|---|---|
| 4 | 30 |
| 5 | 61 |
| 6 | 125 |
| 7 | 253 |
| 8 | 509 |
| 9 | 1.020 |
| 10 | 2.044 |
| 11 | 4.092 |
| 12 | 8.188 |
| 13 | 16.379 |
| 14 | 32.763 |
| 15 | 65.531 |
| 16 | 131.067 |
| ... | ... |
| 20 | 2.097.146 |
| ... | ... |
| 24 | 33.554.425 |
Как видим, снижение стойкости с определенного момента нарастает очень медленно. Более того, количество итераций в точности следует степеням двойки:
 . Во всех случаях, когда наблюдаются подобные закономерности, их можно доказать аналитически, но я уже не ставил это своей целью. Таким образом, не снижая стойкость алгоритма более 16 бит (а по моему твердому убеждению для 128-битных хеш-функций – это никак не скажется на практической их стойкости на ближайшие скажем 25 лет), можно выполнить 130.000 итераций хеширования пароля. Для 256-битных хеш-функций (SHA-256, ГОСТ Р 34.11, RIPEMD-256 и т.п.), очевидно, эта планка еще во много раз выше.
. Во всех случаях, когда наблюдаются подобные закономерности, их можно доказать аналитически, но я уже не ставил это своей целью. Таким образом, не снижая стойкость алгоритма более 16 бит (а по моему твердому убеждению для 128-битных хеш-функций – это никак не скажется на практической их стойкости на ближайшие скажем 25 лет), можно выполнить 130.000 итераций хеширования пароля. Для 256-битных хеш-функций (SHA-256, ГОСТ Р 34.11, RIPEMD-256 и т.п.), очевидно, эта планка еще во много раз выше.Проверка адекватности модели
Как всегда после большого количества теоретических измышлений, возникает желание хоть как то оценить, насколько далека полученная теория от практики. В качестве подопытной хеш-функции мною были взяты первые 16 бит от MD5 (криптостойкая хеш-функция позволяет выбирать любой набор бит результата для формирования усеченной хеш-функции с аналогичными свойствами, хотя и, естественно, меньшей стойкости – соответственно своей новой разрядности). На вход алгоритма подаются все возможные значения от 0 до 0xFFFF, над каждым из значений проводится i итераций, каждая итерация заключается в вычислении первых 16 бит MD5-результата (получается 16-разрядная хеш-функция). «Результаты опытов» приведены в таблице:
| Планируемое снижение стойкости, r (бит) | Кол-во итераций, i | Ожидаемое кол-во элементов в множестве | Наблюдаемое кол-во элементов в множестве |
|---|---|---|---|
| 4 | 30 | 216-4=4.096 | 3.819 |
| 6 | 125 | 216-6=1.024 | 831 |
| 8 | 509 | 216-8=256 | 244 |
Конечно, при таком малом значении N и особенно kN начинает сразу сказываться тот факт, что все выкладки выше приведены для пределов (для N сравнимых и больших 2128 – там всё хорошо). Но даже и здесь общая тенденция прослеживается и приемлемо укладывается в полученные выше формулы.
Следствие – стойкость к словарной атаке
Пришло время проанализировать, «ощутимо ли сужение области значений в тех случаях, когда в качестве парольной фразы выбран словарный или легко конструируемый пароль?». Очевидно, что в этом случае «активное» входное множество значений уже чрезвычайно сужено – оно находится в зависимости от методик подбора в диапазоне от 216 до 248. Таким образом, мы сразу попадаем в «разряженную» ситуацию – в правую часть графика. Здесь вероятность отображения двух разных входных элементов на один и тот же выходной чрезвычайно мала. Миллионы и миллионы операций практически нисколько не изменят количество элементов в выходном множестве. Отсеются единицы/десятки – ни о каком практическом снижении стойкости речи не идет.
Выводы
Описанную схему защиты от brute force-а можно свободно применять на практике практически без ограничений со стороны криптографической стойкости. Рекомендуемые верхние пределы количества итераций (разрешенное снижение стойкости r выбрано субъективно в размере 1/8 разрядности хеш-функции) приведены в таблице:
| Разрядность хеш-функции (бит) | Разрешенное снижение стойкости, r (бит) | Верхний предел разрешенного количества итераций, i |
|---|---|---|
| 128 | 16 | 130.000 |
| 160 | 20 | 2.000.000 |
| 192 | 24 | 32.000.000 |
| 224 | 28 | 500.000.000 |
| 256 | 32 | 8.000.000.000 |
