Декодирование JPEG для чайников

[FF D8]

Вам когда-нибудь хотелось узнать как устроен jpg-файл? Сейчас разберемся! Прогревайте ваш любимый компилятор и hex-редактор, будем декодировать это:

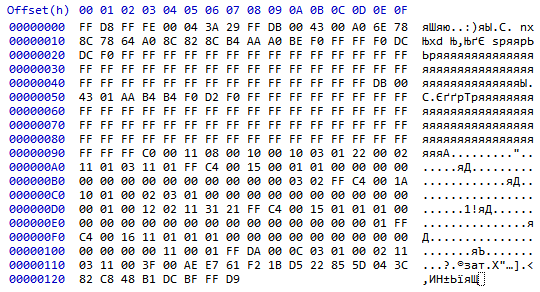
Специально взял рисунок поменьше. Это знакомый, но сильно пережатый favicon Гугла:

Последующее описание упрощено, и приведенная информация не полная, но зато потом будет легко понять спецификацию.

Даже не зная, как происходит кодирование, мы уже можем кое-что извлечь из файла.

[FF D8] — маркер начала. Он всегда находится в начале всех jpg-файлов.

Следом идут байты [FF FE]. Это маркер, означающий начало секции с комментарием. Следующие 2 байта [00 04] — длина секции (включая эти 2 байта). Значит в следующих двух [3A 29] — сам комментарий. Это коды символов ":" и ")", т.е. обычного смайлика. Вы можете увидеть его в первой строке правой части hex-редактора.

Немного теории

Очень кратко:

• Обычно изображение преобразуется из цветового пространства RGB в YCbCr.
• Часто каналы Cb и Cr прореживают, то есть блоку пикселей присваивается усредненное значение. Например, после прореживания в 2 раза по вертикали и горизонтали, пиксели будут иметь такое соответствие:

• Затем значения каналов разбиваются на блоки 8x8 (все видели эти квадратики на слишком сжатом изображении).
• Каждый блок подвергается дискретно-косинусному преобразованию (ДКП), являющемся разновидностью дискретного преобразования Фурье. Получим матрицу коэффициетов 8x8. Причем левый верхний коэффициент называется DC-коффициентом (он самый важный и является усредненным значением всех значений), а оставшиеся 63 — AC-коэффициентами.
• Получившиеся коэффициенты квантуются, т.е. каждый умножается на коэффициент матрицы квантования (каждый кодировщик обычно использует свою матрицу квантования).
• Затем они кодируются кодами Хаффмана.

Закодированные данные располагаются поочередно, небольшими частями:

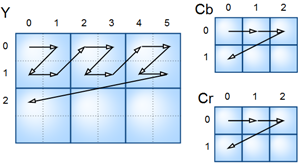
Каждый блок Y_ij, Cb_ij, Cr_ij — это матрица коэффициентов ДКП (так же 8x8), закодированная кодами Хаффмана. В файле они располагаются в таком порядке: Y₀₀Y₁₀Y₀₁Y₁₁Cb₀₀Cr₀₀Y₂₀...

Чтение файла

Файл поделен на секторы, предваряемые маркерами. Маркеры имеют длину 2 байта, причем первый байт [FF]. Почти все секторы хранят свою длину в следующих 2 байта после маркера. Для удобства подсветим маркеры:

Маркер [FF DB]: DQT — таблица квантования

• [00 43] Длина: 0x43 = 67 байт
• [0_] Длина значений в таблице: 0 (0 — 1 байт, 1 — 2 байта)
• [_0] Идентификатор таблицы: 0

Оставшимися 64-мя байтами нужно заполнить таблицу 8x8.

[A0 6E 64 A0 F0 FF FF FF]
[78 78 8C BE FF FF FF FF]
[8C 82 A0 F0 FF FF FF FF]
[8C AA DC FF FF FF FF FF]
[B4 DC FF FF FF FF FF FF]
[F0 FF FF FF FF FF FF FF]
[FF FF FF FF FF FF FF FF]
[FF FF FF FF FF FF FF FF]

Приглядитесь, в каком порядке заполнены значения таблицы. Этот порядок называется zigzag order:

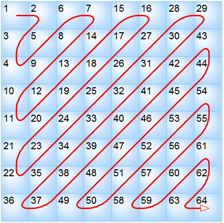
Маркер [FF C0]: SOF0 — Baseline DCT

Этот маркер называется SOF0, и означает, что изображение закодировано базовым методом. Он очень распространен. Но в интернете не менее популярен знакомый вам progressive-метод, когда сначала загружается изображение с низким разрешением, а потом и нормальная картинка. Это позволяет понять что там изображено, не дожидаясь полной загрузки. Спецификация определяет еще несколько, как мне кажется, не очень распространенных методов.

• [00 11] Длина: 17 байт.
• [08] Precision: 8 бит. В базовом методе всегда 8. Это разрядность значений каналов.
• [00 10] Высота рисунка: 0x10 = 16
• [00 10] Ширина рисунка: 0x10 = 16
• [03] Количество каналов: 3. Чаще всего это Y, Cb, Cr или R, G, B

1-й канал:

• [01] Идентификатор: 1
• [2_] Горизонтальное прореживание (H1): 2
• [_2] Вертикальное прореживание (V1): 2
• [00] Идентификатор таблицы квантования: 0

2-й канал:

• [02] Идентификатор: 2
• [1_] Горизонтальное прореживание (H2): 1
• [_1] Вертикальное прореживание (V2): 1
• [01] Идентификатор таблицы квантования: 1

3-й канал:

• [03] Идентификатор: 3
• [1_] Горизонтальное прореживание (H3): 1
• [_1] Вертикальное прореживание (V3): 1
• [01] Идентификатор таблицы квантования: 1

Находим H_max=2 и V_max=2. Канал i будет прорежен в H_max/H_i раз по горизонтали и V_max/V_i раз по вертикали.

Маркер [FF C4]: DHT (таблица Хаффмана)

Эта секция хранит коды и значения, полученные кодированием Хаффмана.

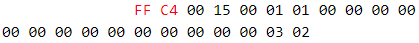
• [00 15] Длина: 21 байт
• [0_] Класс: 0 (0 — таблица DC коэффициентов, 1 — таблица AC коэффициентов).
• [_0] Идентификатор таблицы: 0

Следующие 16 значений:

Длина кода Хаффмана: 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16
Количество кодов:  [01 01 00 00 00 00 00 00 00 00 00 00 00 00 00 00]

Количество кодов означает количество кодов такой длины. Обратите внимание, что секция хранит только длины кодов, а не сами коды. Мы должны найти коды сами. Итак, у нас есть один код длины 1 и один — длины 2. Итого 2 кода, больше кодов в этой таблице нет.
С каждым кодом сопоставлено значение, в файле они перечислены следом. Значения однобайтовые, поэтому читаем 2 байта:

• [03] — значение 1-го кода
• [02] — значение 2-го кода

Далее в файле можно видеть еще 3 маркера [FF C4], я пропущу разбор соответствующих секций, он аналогичен вышеприведенному.

Построение дерева кодов Хаффмана

Мы должны построить бинарное дерево по таблице, которую мы получили в секции DHT. А уже по этому дереву мы узнаем каждый код. Значения добавляем в том порядке, в каком указаны в таблице. Алгоритм прост: в каком бы узле мы ни находились, всегда пытаемся добавить значение в левую ветвь. А если она занята, то в правую. А если и там нет места, то возвращаемся на уровень выше, и пробуем оттуда. Остановиться нужно на уровне равном длине кода. Левым ветвям соответствует значение 0, правым — 1.

Деревья для всех таблиц этого примера:

В кружках — значения кодов, под кружками — сами коды (поясню, что мы получили их, пройдя путь от вершины до каждого узла). Именно такими кодами закодировано само содержимое рисунка.

Маркер [FF DA]: SOS (Start of Scan)

Байт [DA] в маркере означает — «ДА! Наконец-то то мы перешли к финальной секции!». Однако секция символично называется SOS.

• [00 0C] Длина: 12 байт.
• [03] Количество каналов. У нас 3, по одному на Y, Cb, Cr.

1-й канал:

• [01] Идентификатор канала: 1 (Y)
• [0_] Идентификатор таблицы Хаффмана для DC коэффициентов: 0
• [_0] Идентификатор таблицы Хаффмана для AC коэффициентов: 0

2-й канал:

• [02] Идентификатор канала: 2 (Cb)
• [1_] Идентификатор таблицы Хаффмана для DC коэффициентов: 1
• [_1] Идентификатор таблицы Хаффмана для AC коэффициентов: 1

3-й канал:

• [03] Идентификатор канала: 3 (Cr)
• [1_] Идентификатор таблицы Хаффмана для DC коэффициентов: 1
• [_1] Идентификатор таблицы Хаффмана для AC коэффициентов: 1

[00], [3F], [00] — Start of spectral or predictor selection, End of spectral selection, Successive approximation bit position. Эти значения используются только для прогрессивного режима, что выходит за рамки статьи.

Отсюда и до конца (маркера [FF D9]) закодированные данные.

Закодированные данные

Последующие значения нужно рассматривать как битовый поток. Первых 33 бит будет достаточно, чтобы построить первую таблицу коэффициентов:

Нахождение DC-коэффициента

1) Читаем последовательность битов (если встретим 2 байта [FF 00], то это не маркер, а просто байт [FF]). После каждого бита сдвигаемся по дереву Хаффмана (с соответствующим идентификатором) по ветви 0 или 1, в зависимости от прочитанного бита. Останавливаемся, если оказались в конечном узле.

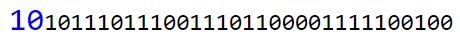
2) Берем значение узла. Если оно равно 0, то коэффициент равен 0, записываем в таблицу и переходим к чтению других коэффициентов. В нашем случае — 02. Это значение — длина коэффициента в битах. Т. е. читаем следующие 2 бита, это и будет коэффициент:

3) Если первая цифра значения в двоичном представлении — 1, то оставляем как есть: DC = <значение>. Иначе преобразуем: DC = <значение>-2^<длина значения>+1. Записываем коэффициент в таблицу в начало зигзага — левый верхний угол.

Нахождение AC-коэффициентов

1) Аналогичен п. 1, нахождения DC коэффициента. Продолжаем читать последовательность:

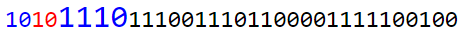
2) Берем значение узла. Если оно равно 0, это означает, что оставшиеся значения матрицы нужно заполнить нулями. Дальше закодирована уже следующая матрица. В нашем случае значение узла: 0x31.

• Первый полубайт: 0x3 — именно столько нулей мы должны добавить в матрицу. Это 3 нулевых коэффициента.
• Второй полубайт: 0x1 — длина коэффициента в битах. Читаем следующий бит.

1. Аналогичен п. 3 нахождения DC-коэффициента.

Читать AC-коэффициенты нужно пока не наткнемся на нулевое значение кода, либо пока не заполнится матрица.
В нашем случае мы получим:

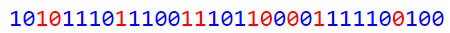
и матрицу:

[2  0  3 0 0 0 0 0]
[0  1  2 0 0 0 0 0]
[0 -1 -1 0 0 0 0 0]
[1  0  0 0 0 0 0 0]
[0  0  0 0 0 0 0 0]
[0  0  0 0 0 0 0 0]
[0  0  0 0 0 0 0 0]
[0  0  0 0 0 0 0 0]

Вы заметили, что значения заполнены в том же зигзагообразном порядке? Причина использования такого порядка простая — так как чем больше значения v и u, тем меньшей значимостью обладает коэффициент Svu в дискретно-косинусном преобразовании. Поэтому, при высоких степенях сжатия малозначащие коэффициенты обнуляют, тем самым уменьшая размер файла.

Аналогично получаем еще 3 матрицы Y-канала…

[-4  1 1 1 0 0 0 0] [ 5 -1  1 0 0 0 0 0] [-4  2  2 1 0 0 0 0]
[ 0  0 1 0 0 0 0 0] [-1 -2 -1 0 0 0 0 0] [-1  0 -1 0 0 0 0 0]
[ 0 -1 0 0 0 0 0 0] [ 0 -1  0 0 0 0 0 0] [-1 -1  0 0 0 0 0 0]
[ 0  0 0 0 0 0 0 0] [-1  0  0 0 0 0 0 0] [ 0  0  0 0 0 0 0 0]
[ 0  0 0 0 0 0 0 0] [ 0  0  0 0 0 0 0 0] [ 0  0  0 0 0 0 0 0]
[ 0  0 0 0 0 0 0 0] [ 0  0  0 0 0 0 0 0] [ 0  0  0 0 0 0 0 0]
[ 0  0 0 0 0 0 0 0] [ 0  0  0 0 0 0 0 0] [ 0  0  0 0 0 0 0 0]
[ 0  0 0 0 0 0 0 0] [ 0  0  0 0 0 0 0 0] [ 0  0  0 0 0 0 0 0]

Но! Закодированные DC-коэффициенты — это не сами DC-коэффициенты, а их разности между коэффициентами предыдущей таблицы (того же канала)! Нужно поправить матрицы:

• DC для 2-ой: 2 + (-4) = -2
• DC для 3-ой: -2 + 5 = 3
• DC для 4-ой: 3 + (-4) = -1

[-2  1 1 1 0 0 0 0] [ 3 -1  1 0 0 0 0 0] [-1  2  2 1 0 0 0 0]
[ 0  0 1 0 0 0 0 0] [-1 -2 -1 0 0 0 0 0] [-1  0 -1 0 0 0 0 0]
[ 0 -1 0 0 0 0 0 0] [ 0 -1  0 0 0 0 0 0] [-1 -1  0 0 0 0 0 0]
[ 0  0 0 0 0 0 0 0] [-1  0  0 0 0 0 0 0] [ 0  0  0 0 0 0 0 0]
[ 0  0 0 0 0 0 0 0] [ 0  0  0 0 0 0 0 0] [ 0  0  0 0 0 0 0 0]
[ 0  0 0 0 0 0 0 0] [ 0  0  0 0 0 0 0 0] [ 0  0  0 0 0 0 0 0]
[ 0  0 0 0 0 0 0 0] [ 0  0  0 0 0 0 0 0] [ 0  0  0 0 0 0 0 0]
[ 0  0 0 0 0 0 0 0] [ 0  0  0 0 0 0 0 0] [ 0  0  0 0 0 0 0 0]

Теперь порядок. Это правило действует до конца файла.

… и по матрице для Cb и Cr:

[-1 0 0 0 0 0 0 0] [0  0 0 0 0 0 0 0]
[ 1 1 0 0 0 0 0 0] [1 -1 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0] [1  0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0] [0  0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0] [0  0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0] [0  0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0] [0  0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0] [0  0 0 0 0 0 0 0]

Вычисления

Квантование

Вы помните, что матрица проходит этап квантования? Элементы матрицы нужно почленно перемножить с элементами матрицы квантования. Осталось выбрать нужную. Сначала мы просканировали первый канал. Он использует матрицу квантования 0 (у нас она первая из двух). Итак, после перемножения получаем 4 матрицы Y-канала:

[320    0  300 0 0 0 0 0] [-320  110 100 160 0 0 0 0]
[  0  120  280 0 0 0 0 0] [   0    0 140   0 0 0 0 0]
[  0 -130 -160 0 0 0 0 0] [   0 -130   0   0 0 0 0 0]
[140    0    0 0 0 0 0 0] [   0    0   0   0 0 0 0 0]
[  0    0    0 0 0 0 0 0] [   0    0   0   0 0 0 0 0]
[  0    0    0 0 0 0 0 0] [   0    0   0   0 0 0 0 0]
[  0    0    0 0 0 0 0 0] [   0    0   0   0 0 0 0 0]
[  0    0    0 0 0 0 0 0] [   0    0   0   0 0 0 0 0]

[ 480 -110  100 0 0 0 0 0] [-160  220  200 160 0 0 0 0]
[-120 -240 -140 0 0 0 0 0] [-120    0 -140   0 0 0 0 0]
[   0 -130    0 0 0 0 0 0] [-140 -130    0   0 0 0 0 0]
[-140    0    0 0 0 0 0 0] [   0    0    0   0 0 0 0 0]
[   0    0    0 0 0 0 0 0] [   0    0    0   0 0 0 0 0]
[   0    0    0 0 0 0 0 0] [   0    0    0   0 0 0 0 0]
[   0    0    0 0 0 0 0 0] [   0    0    0   0 0 0 0 0]
[   0    0    0 0 0 0 0 0] [   0    0    0   0 0 0 0 0]

… и по матрице для Cb и Cr.

[-170   0 0 0 0 0 0 0] [  0    0 0 0 0 0 0 0]
[ 180 210 0 0 0 0 0 0] [180 -210 0 0 0 0 0 0]
[   0   0 0 0 0 0 0 0] [240    0 0 0 0 0 0 0]
[   0   0 0 0 0 0 0 0] [  0    0 0 0 0 0 0 0]
[   0   0 0 0 0 0 0 0] [  0    0 0 0 0 0 0 0]
[   0   0 0 0 0 0 0 0] [  0    0 0 0 0 0 0 0]
[   0   0 0 0 0 0 0 0] [  0    0 0 0 0 0 0 0]
[   0   0 0 0 0 0 0 0] [  0    0 0 0 0 0 0 0]

Обратное дискретно-косинусное преобразование

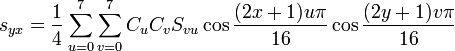
Формула не должна доставить сложностей. S_vu — наша полученная матрица коэффициентов. u — столбец, v — строка. C_x = 1/√2 для x = 0, а в остальных случаях = 1. s_yx — непосредственно значения каналов.

Приведу результат вычисления только первой матрицы канала Y (после обязательного округления):

[138  92 27 -17 -17 28  93 139]
[136  82  5 -51 -55 -8  61 111]
[143  80 -9 -77 -89 -41 32  86]
[157  95  6 -62 -76 -33 36  86]
[147 103 37 -12 -21  11 62 100]
[ 87  72 50  36  37  55 79  95]
[-10   5 31  56  71  73 68  62]
[-87 -50  6  56  79  72 48  29]

и для Cb Cr:

[  60  52  38  20   0 -18 -32 -40] [ 19  27  41  60  80  99 113 120]
[  48  41  29  13  -3 -19 -31 -37] [  0   6  18  34  51  66  78  85]
[  25  20  12   2  -9 -19 -27 -32] [-27 -22 -14  -4   7  17  25  30]
[  -4  -6  -9 -13 -17 -20 -23 -25] [-43 -41 -38 -34 -30 -27 -24 -22]
[ -37 -35 -33 -29 -25 -21 -18 -17] [-35 -36 -39 -43 -47 -51 -53 -55]
[ -67 -63 -55 -44 -33 -22 -14 -10] [ -5  -9 -17 -28 -39 -50 -58 -62]
[ -90 -84 -71 -56 -39 -23 -11  -4] [ 32  26  14  -1 -18 -34 -46 -53]
[-102 -95 -81 -62 -42 -23  -9  -1] [ 58  50  36  18  -2 -20 -34 -42]

Ко всем полученным значениям нужно прибавить по 128, а затем ограничить их диапазон от 0 до 255:

Y  = min(max(0, Y  + 128), 255)
Cb = min(max(0, Cb + 128), 255)
Cr = min(max(0, Cr + 128), 255)

Например: 138 → 266 → 255, 92 → 220 → 220 и т. д.

YCbCr в RGB

4 матрицы Y, и по одной Cb и Cr, так как мы прореживали каналы и 4 пикселям Y соответствует по одному Cb и Cr. Поэтому вычислять так: YCbCrToRGB(Y[y,x], Cb[y/2, x/2], Cr[y/2, x/2]):

function YCbCrToRGB(Y, Cb, Cr)
{
    R = round(Y                      + 1.402   * (Cr-128))
    G = round(Y - 0.34414 * (Cb-128) - 0.71414 * (Cr-128))
    B = round(Y + 1.772   * (Cb-128)                     )

    R = min(max(0, R), 255)
    G = min(max(0, G), 255)
    B = min(max(0, B), 255)

    return R, G, B
}

// Псевдокод для нашего рисунка
for (y = 0; y < 16; ++y)
    for (x = 0; x < 16; ++x)
        R, G, B = YCbCrToRGB(Y[y,x], Cb[y/2, x/2], Cr[y/2, x/2])

Вот полученные таблицы для каналов R, G, B для левого верхнего квадрата 8x8 нашего примера:

R:
255 249 195 149 169 215 255 255
255 238 172 116 131 179 255 255
255 209 127  58  64 112 209 255
255 224 143  73  76 120 212 255
217 193 134  84  86 118 185 223
177 162 147 132 145 162 201 218
 57  74 101 125 144 146 147 142
  0  18  76 125 153 146 128 108

G:
220 186 118  72  67 113 172 205
220 175  95  39  29  77 139 190
238 192 100  31  16  64 132 185
238 207 116  46  28  72 135 186
255 242 175 125 113 145 193 231
226 211 188 173 172 189 209 226
149 166 192 216 230 232 225 220
 73 110 167 216 239 232 206 186

B:
255 255 250 204 179 225 255 255
255 255 227 171 141 189 224 255
255 255 193 124  90 138 186 239
255 255 209 139 102 146 189 240
255 255 203 153 130 162 195 233
255 244 216 201 189 206 211 228
108 125 148 172 183 185 173 168
 32  69 123 172 192 185 154 134

Конец

Вообще я не специалист по JPEG, поэтому вряд ли смогу ответить на все вопросы. Просто когда я писал свой декодер, мне часто приходилось сталкиваться с различными непонятными проблемами. И когда изображение выводилось некорректно, я не знал где допустил ошибку. Может неправильно проинтерпретировал биты, а может неправильно использовал ДКП. Очень не хватало пошагового примера, поэтому, надеюсь, эта статья поможет при написании декодера. Думаю, она покрывает описание базового метода, но все-равно нельзя обойтись только ей. Предлагаю вам ссылки, которые помогли мне:

• ru.wikipedia.org/JPEG — для поверхностного ознакомления
• en.wikipedia.org/JPEG — гораздо более толковая статья о процессах кодирования/декодирования
• JPEG Standard (JPEG ISO/IEC 10918-1 ITU-T Recommendation T.81) — не обойтись без 186-страничной спецификации
• impulseadventure.com/photo — Хорошие подробные статьи. По примерам я разобрался как строить деревья Хаффмана и использовать их при чтении соответствующей секции
• JPEGsnoop — На том же сайте есть отличная утилита, которая вытаскивает всю информацию jpeg-файла

[FF D9]