Предлагаемый ниже нерекурсивный алгоритм несколько отличается от изложенных в книге Липского [1] и обнаруженных мной в русскоязычном сегменте интернета. Надеюсь будет интересно.
Кратко постановка задачи. Имеется множество размерности N. Необходимо получить все N! возможных перестановок.
Далее, для простоты, используем в качестве множества целые числа (1..N). Вместо чисел можно использовать любые объекты, т.к. операций сравнения элементов множества в алгоритме нет.
Для хранения промежуточных данных сформируем структуру данных следующего вида:
и заполним ее первоначальными значениями
Номер элемента в массиве masiv будем далее называть уровнем.
В список первого уровня заносим все элементы множества. На первом уровне размерность списка равна N и сам список не изменяется по всему ходу выполнения алгоритма. При первичном заполнении все указатели в массиве устанавливаются на первый элемент в списке.
На каждом следующем уровне его список формируется на основании списка предыдущего уровня, но без одного элемента, который помечен указателем. На предпоследнем уровне (N-2) список содержит три элемента. На последнем уровне (N-1) список содержит два элемента. Список нижнего уровня формируется как список предыдущего уровня без элемента, на который указывает указатель предыдущего уровня.
В результате первичного заполнения получены две первых перестановки.Это общий массив сформированный на верхних уровнях ( 1… (N-2)) из элементов списка на которые указывают указатели.
и из списка последнего уровня- две пары элементов в разном порядке ( два хвостика 1 2 и 2 1)
Все дальнейшие перестановки формируются также, всегда с предпоследнего уровня (N-2),
Порядок получения последующих перестановок состоит в том, что находясь на предпоследнем уровне (N-2) и сформировав две перестановки пытаемся увеличить указатель выбранного элемента на 1.
Если это возможно, то на последнем уровне меняем список и повторяемся.
Если на предпоследнем уровне увеличить указатель не удается (перебраны все возможные варианты ), то поднимаемся до уровня на котором увеличение указателя (перемещение вправо) возможно. Условие окончания работы алгоритма — указатель на первом уровне выходит за N.
После сдвига указателя вправо меняем список под ним и двигаемся вниз до предпоследнего уровня (N-2) также обновляя списки и устанавливая указатели выбранного элемента в 1.
Более наглядно и понятно работа алгоритма представлена на рисунке ниже ( для размерности множества N =5). Номер на рисунке соответствует уровню в описании. Возможно даже, что кроме рисунка для понимания алгоритма ничего и не надо.
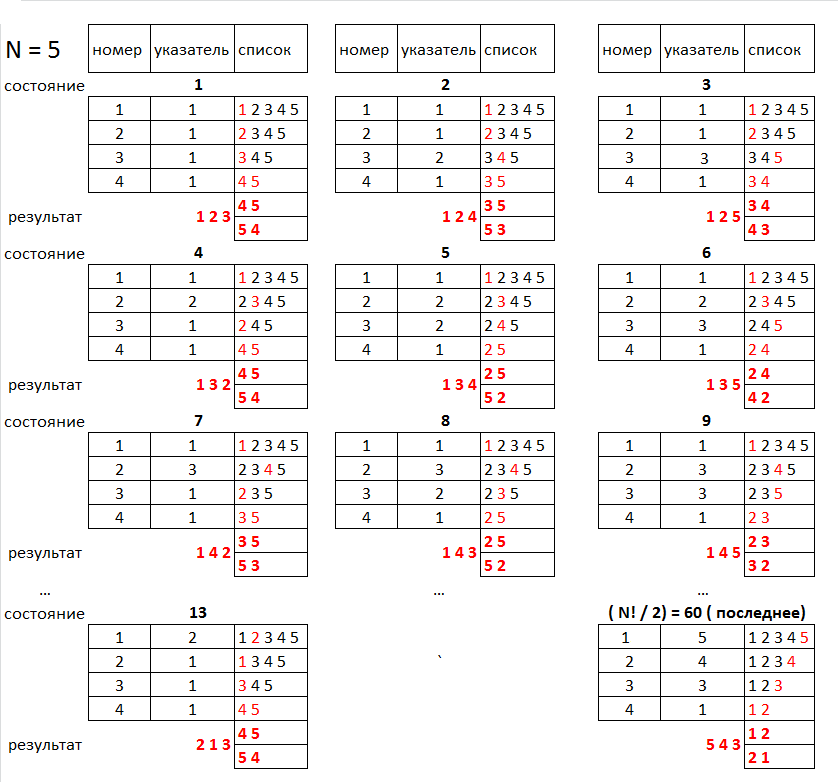
Конечно, при реализации алгоритма можно было использовать и обычный двухмерный массив, тем более что для небольших N выигрыш объема памяти ничего не дает, а на больших N мы можем не дождаться окончания работы алгоритма.
Один из способов реализации алгоритма на VBA ниже. Для его запуска можно создать книгу Excel с макросами, создать модуль на вкладке разработчик VB и скопировать текст в модуль. После запуска generate() на Лист1 будут выведены все перестановки.
Ссылки:
[1] В.Липский. Комбинаторика для программистов. -Москва, издательство Мир, 1988.
Кратко постановка задачи. Имеется множество размерности N. Необходимо получить все N! возможных перестановок.
Далее, для простоты, используем в качестве множества целые числа (1..N). Вместо чисел можно использовать любые объекты, т.к. операций сравнения элементов множества в алгоритме нет.
Для хранения промежуточных данных сформируем структуру данных следующего вида:
type dtree ukaz as integer ' номер выбранного элемента в списке spisok() as integer ' список доступных значений end type
и заполним ее первоначальными значениями
Dim masiv(N-) As dtree ' размерность массива = N-1 For ii = 1 To N - 1 masiv(ii).ukaz = 1 ReDim masiv(ii).spisok(N + 1 - ii) ' устанавливаем размерность списка For kk = 1 To (N + 1 - ii) masiv(ii).spisok(kk) = kk + ii - 1 Next Next
Номер элемента в массиве masiv будем далее называть уровнем.
В список первого уровня заносим все элементы множества. На первом уровне размерность списка равна N и сам список не изменяется по всему ходу выполнения алгоритма. При первичном заполнении все указатели в массиве устанавливаются на первый элемент в списке.
На каждом следующем уровне его список формируется на основании списка предыдущего уровня, но без одного элемента, который помечен указателем. На предпоследнем уровне (N-2) список содержит три элемента. На последнем уровне (N-1) список содержит два элемента. Список нижнего уровня формируется как список предыдущего уровня без элемента, на который указывает указатель предыдущего уровня.
В результате первичного заполнения получены две первых перестановки.Это общий массив сформированный на верхних уровнях ( 1… (N-2)) из элементов списка на которые указывают указатели.
For ii = 1 To N-2 massiv(ii).spisok(ukaz) Next
и из списка последнего уровня- две пары элементов в разном порядке ( два хвостика 1 2 и 2 1)
+ massiv(N-1).spisok(1) + massiv(N-1).spisok(2) + massiv(N-1).spisok(2) + massiv(N-1).spisok(1)
Все дальнейшие перестановки формируются также, всегда с предпоследнего уровня (N-2),
Порядок получения последующих перестановок состоит в том, что находясь на предпоследнем уровне (N-2) и сформировав две перестановки пытаемся увеличить указатель выбранного элемента на 1.
Если это возможно, то на последнем уровне меняем список и повторяемся.
Если на предпоследнем уровне увеличить указатель не удается (перебраны все возможные варианты ), то поднимаемся до уровня на котором увеличение указателя (перемещение вправо) возможно. Условие окончания работы алгоритма — указатель на первом уровне выходит за N.
После сдвига указателя вправо меняем список под ним и двигаемся вниз до предпоследнего уровня (N-2) также обновляя списки и устанавливая указатели выбранного элемента в 1.
Более наглядно и понятно работа алгоритма представлена на рисунке ниже ( для размерности множества N =5). Номер на рисунке соответствует уровню в описании. Возможно даже, что кроме рисунка для понимания алгоритма ничего и не надо.

Конечно, при реализации алгоритма можно было использовать и обычный двухмерный массив, тем более что для небольших N выигрыш объема памяти ничего не дает, а на больших N мы можем не дождаться окончания работы алгоритма.
Один из способов реализации алгоритма на VBA ниже. Для его запуска можно создать книгу Excel с макросами, создать модуль на вкладке разработчик VB и скопировать текст в модуль. После запуска generate() на Лист1 будут выведены все перестановки.
VBA для Excel
Option Explicit Type dtree tek_elem_ukaz As Integer spisok() As Integer End Type Dim masiv() As dtree Dim start_print As Integer Dim N As Integer Sub generate() Dim ii As Integer, kk As Integer, jj As Integer Dim uroven As Integer Лист1.Cells.Clear N = 5 start_print = 1 ReDim masiv(N - 1) ' первичное заполнение For ii = 1 To N - 1 masiv(ii).tek_elem_ukaz = 1 ReDim masiv(ii).spisok(N + 1 - ii) For kk = 1 To (N + 1 - ii) masiv(ii).spisok(kk) = kk + ii - 1 Next Next uroven = N - 2 Do ' результат Call print_rezult(uroven) ' на последнем уровне можно сдвинуться вправо If masiv(uroven).tek_elem_ukaz <= (N - uroven) Then ' делаем шаг вправо ' меняем тек элемент masiv(uroven).tek_elem_ukaz = masiv(uroven).tek_elem_ukaz + 1 ' меняем массив снизу Call zap_niz(uroven) Else ' делаем шаг вверх до первого уровня, где можно сдвинуться вправо Do While uroven > 1 And masiv(uroven).tek_elem_ukaz > (N - uroven) uroven = uroven - 1 Loop If uroven = 1 And masiv(1).tek_elem_ukaz = N Then MsgBox "stop calc" Exit Sub ' напечатали все End If ' делаем шаг вправо на первом снизу доступном уровне masiv(uroven).tek_elem_ukaz = masiv(uroven).tek_elem_ukaz + 1 Call zap_niz(uroven) ' заполнение нижних уровней Do While uroven < N - 2 uroven = uroven + 1 masiv(uroven + 1).tek_elem_ukaz = 1 ' меняем массив снизу For kk = 2 To N - uroven + 1 masiv(uroven + 1).spisok(kk - 1) = masiv(uroven).spisok(kk) Next Loop End If Loop End Sub Sub print_rezult(ukaz As Integer) Dim ii As Integer For ii = 1 To ukaz With masiv(ii) Лист1.Cells(start_print, ii) = .spisok(.tek_elem_ukaz) Лист1.Cells(start_print + 1, ii) = .spisok(.tek_elem_ukaz) End With Next With masiv(ukaz + 1) Лист1.Cells(start_print, ukaz + 1) = .spisok(1) Лист1.Cells(start_print, ukaz + 2) = .spisok(2) start_print = start_print + 1 Лист1.Cells(start_print, ukaz + 1) = .spisok(2) Лист1.Cells(start_print, ukaz + 2) = .spisok(1) start_print = start_print + 1 End With End Sub Sub zap_niz(ukaz As Integer) ' заполнение нижнего уровня Dim ii As Integer, wsp1 As Integer ' меняем тек элемент wsp1 = masiv(ukaz).tek_elem_ukaz masiv(ukaz + 1).tek_elem_ukaz = 1 ' меняем массив снизу For ii = 1 To wsp1 - 1 masiv(ukaz + 1).spisok(ii) = masiv(ukaz).spisok(ii) Next For ii = wsp1 + 1 To N - ukaz + 1 masiv(ukaz + 1).spisok(ii - 1) = masiv(ukaz).spisok(ii) Next End Sub
Ссылки:
[1] В.Липский. Комбинаторика для программистов. -Москва, издательство Мир, 1988.
