В данной публикации я хотел бы представить ряд идей и опыт практического воплощения элемента теории Хаоса — фрактального преобразования в проекте разработке нового алгоритма сжатия аудио данных.
Чего вы не найдёте здесь:
Что вы найдёте здесь:
Думаю, что для большинства читателей этой публикации данная задача покажется странной. Обычно, понятие фрактала связывают с красивыми картинками — результатами выполнения фрактальных преобразований, именуемыми также фрактальными (или «странными») аттракторами. Однако, внимательное изучение фрактальных преобразований позволяет понять, что фракталы это не только красивые изображения. Фрактальные преобразования определяют проекции элементов в замкнутом множестве. Таким множествами могут быть цветные точки в 2.5 D пространстве, набор точек на 2 D плоскости, или набор дискретных выборок аудио потока в 1.5 D пространстве.
Я заинтересовался фрактальными преобразованиями с момента написания диссертации на соискания степени кандидата технических наук. Тема диссертации была — «Алгоритмы сокращения вычислительной сложности фрактального анализа в системах обработки визуальных данных». Диссертация была с успехом защищена и принята к публикации LAP LAMBERT Academic Publishing. Иногда встречаю ссылки на неё на сайтах Amazon и Ozon.
Я потратил много времени на изучение как теоретических основ, так и практических результатов исследований фрактальных преобразований и обнаружил только две попытки развития фрактальных преобразований до уровня индустриальных стандартов:
Однако, данные попытки не привели к значительному успеху. Причиной провалов послужила значительная вычислительная сложность.
Построение изображений на основе фрактальных преобразований не представляет математической сложности. Известный фрактал (фрактальное множество) Манделброта строится исходя из следующего преобразования:
Z(n+1) = Zn^2 + C where n = 1, 2, 3,…

Таким образом, очень сложная визуализация может быть достигнута очень простым выражением. Это приводит к следующему вопросу — возможно ли построить реальное изображение посредством фрактального преобразования? Данный вопрос был разрешён утвердительно. Более точно, можно найти такое фрактальное преобразование, которое способно построить изображение с искажениями меньшем или равными любому предопределённому значению. Это означает, что сгенерированное изображение может отличаться от оригинального на величину, неотличимую зрителем благодаря избыточности визуальной информации изображения. Таким образом, фрактальное кодирование изображения является технологией обработки изображения с потерей качества.
В книге — Amazon или Ozon можно найти точное доказательства применимости фрактального преобразования к задачам обработки изображений – теорема «Коллажа» Майкла Брансли.
Вы можете спросить – как выполнить фрактальное кодирование (или более точно – фрактальный анализ)? Визуализация фрактального множества Мандельброта весьма впечатляет, но оно было разработано после многих лет исследований. Попытка найти подходящее фрактальное преобразование путём простого перебора бесперспективна. Решение данной проблемы было предложено Майклом Брансли и его аспирантами (Майклом Брансли в дальнейшем основал Iterated Systems Incorporated). Они предложили блочную схему фрактального преобразования. С точки зрения выполнения фрактальных преобразований не существует различий в применимости фрактальных преобразований к множеству точек или к множеству блоков точек — partitioned iterated function systems (PIFS). Подобная схема базируется на извлечении копии точек из одной части множества точек, применении преобразований к копии и вставка результат в другую часть множества – это отличает данный подход от фрактальных преобразований для отдельных точек. PIFS схему можно представить в следующем виде:
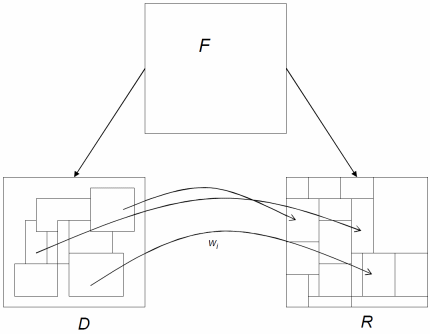
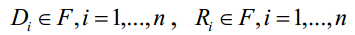
где F – оригинальное множество точек, D и R множества областей точек из F, — преобразование одной области из множества D и область множества R. Множества
— преобразование одной области из множества D и область множества R. Множества  и определяют искомые фрактальные преобразования. Важно отметить, что если фрактальное преобразование для фрактального множества Мандельброта базируется на одном уравнении фрактального преобразования и идеи глобального самоподобия (то есть подобие всего множества любой его части), то PIFS схема базируется на группе фрактальных преобразований и идеи локальном подобии отдельных областей множества.
и определяют искомые фрактальные преобразования. Важно отметить, что если фрактальное преобразование для фрактального множества Мандельброта базируется на одном уравнении фрактального преобразования и идеи глобального самоподобия (то есть подобие всего множества любой его части), то PIFS схема базируется на группе фрактальных преобразований и идеи локальном подобии отдельных областей множества.
Вы можете спросить – как это относится к реальным изображениям? На реальных изображениях маловероятно найти глобальное самоподобие, но возможно установить подобие между разными областями реального изображения при условии допустимого отклонения. Если результирующий объём памяти для хранения системы уравнений фрактальных преобразований меньше объёма памяти для хранения оригинального изображения – то получается сжатие изображения с потерями. Данный подход обработки изображений отличается от классической идеи линейной интерполяции сигналов.
Для понимания данного различия требуется обратить внимание на три главных свойства фрактальных преобразований:
По аналогии с фрактальным преобразованием множества Манделброта, PIFS преобразование для реальных изображений можно представит в следующем виде:
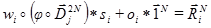
где – преобразование в пространстве точек изображения,
– преобразование в пространстве точек изображения, 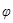 – сжимающее преобразование вектора с длинной
– сжимающее преобразование вектора с длинной 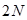 в вектор с длинной
в вектор с длинной 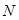 , но что означают переменные
, но что означают переменные 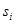 и
и 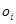 ? Переменные
? Переменные  и
и 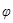 описывают преобразование на плоскости, но каждая точка реального изображения имеет специальное значение – интенсивность собственной яркости которая должна быть рассмотрена как часть пространства фрактального преобразования:
описывают преобразование на плоскости, но каждая точка реального изображения имеет специальное значение – интенсивность собственной яркости которая должна быть рассмотрена как часть пространства фрактального преобразования: 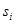 – сжимающее преобразование яркости и
– сжимающее преобразование яркости и 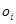 – смещение интенсивности яркости (по аналогии уравнении прямой – f(y) = y*s+o).
– смещение интенсивности яркости (по аналогии уравнении прямой – f(y) = y*s+o).
Что делать с этом уравнением? Очень просто – выполнить данное выражение для всех групп преобразований ( ,
, 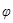 ,
, 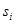 ,
, 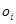 ) что должно заполнить множество R, заполняющее все изображение F. И ещё раз, и ещё раз (рекурсивное выполнение), до бесконечности. В реальности, всё намного проще – после каждого рекурсивного выполнения итерации синтеза фрактального множества расстояние между точками уменьшается (сжимающее свойство фрактального преобразования), но если для аналитического пространства нет ограничений в делимости, то для дискретного пространства цифровых изображений новые точки будут попадать в отсечённое пространство между соседними выборками. Это случится после
) что должно заполнить множество R, заполняющее все изображение F. И ещё раз, и ещё раз (рекурсивное выполнение), до бесконечности. В реальности, всё намного проще – после каждого рекурсивного выполнения итерации синтеза фрактального множества расстояние между точками уменьшается (сжимающее свойство фрактального преобразования), но если для аналитического пространства нет ограничений в делимости, то для дискретного пространства цифровых изображений новые точки будут попадать в отсечённое пространство между соседними выборками. Это случится после 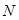 рекурсивных итераций PIFS.
рекурсивных итераций PIFS.
Ожидаемый вопрос – как найти упомянутые коэффициенты ,
, 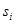 ,
, 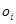 для системы фрактальных преобразований? Задача подобного поиска может быть автоматизирована исходя из следующего уравнения:
для системы фрактальных преобразований? Задача подобного поиска может быть автоматизирована исходя из следующего уравнения:
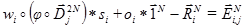
задача поиска заключается в поиске пары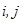 , которая минимизирует длину вектора отклонения
, которая минимизирует длину вектора отклонения 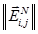 . Если установить экстремальное значение допустимого отклонения равное 0, то можно вывести следующие приближения для
. Если установить экстремальное значение допустимого отклонения равное 0, то можно вывести следующие приближения для 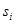 и
и 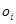 :
:
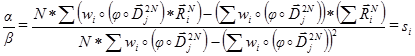
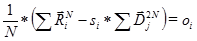
Данные выражения позволяют рассчитать оптимальные значения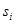 и
и 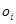 , но неизвестными переменными остаются
, но неизвестными переменными остаются  и пары
и пары 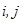 . К сожалению, на настоящий момент отсутствуют аналитические решения для этих переменных – остаётся только задавать множества
. К сожалению, на настоящий момент отсутствуют аналитические решения для этих переменных – остаётся только задавать множества  и пар
и пар 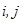 , и перебирать их комбинации для минимизации
, и перебирать их комбинации для минимизации 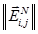 уравнения:
уравнения:
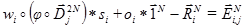
Для эффективной минимизации требуется задавать большие диапазоны значений множества и пар
и пар 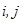 , что ведёт к «комбинаторному взрыву» – необходимости к перебору сотен тысяч всевозможных комбинаций, на что требуется часы работы компьютерного процессора. Именно эта проблема и не позволяет перейти фрактальному анализу изображений из области экзотических исследований в сферу индустриальных стандартов.
, что ведёт к «комбинаторному взрыву» – необходимости к перебору сотен тысяч всевозможных комбинаций, на что требуется часы работы компьютерного процессора. Именно эта проблема и не позволяет перейти фрактальному анализу изображений из области экзотических исследований в сферу индустриальных стандартов.
Предвижу вопрос – всё выше описанное интересно, но причём тут звук и сжатие звуковых данных? Я полагаю многие уже поняли, что для фрактального анализа природа множеств не имеет значения – множество пикселей на плоскости или множество выборок из звукового потока. Если накапливать выборки входного звукового потока в буфере и затем обрабатывать их как отдельные множества, то можно сформировать систем фрактальных преобразований, из которых можно синтезировать фрактальные множества, приближённые к оригинальным выборкам звукового потока. Что и было реализованно в моём проекте, который включает кодер ROAD и декодер (в форме плагина для Winamp) — тестовые аудио файлы: Origa — Inner Universe 4Samples.road.wav и Alpha — Revolution in Paradise 4Samples.road.wav. Новый алгоритм сжатия звуковых данных позволил разработать формат с пятью уникальными свойствами:
Многие математические концепции имеют физические интерпретации. К примеру –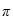 и окружность круга или натуральный логарифм и спиральная раковина моллюска. Часто указывают на связь фрактальных множеств с ростом кристалов или деревьев. Однако я бы хотел бы представить мою собственную интерпретацию фрактальных преобразований.
и окружность круга или натуральный логарифм и спиральная раковина моллюска. Часто указывают на связь фрактальных множеств с ростом кристалов или деревьев. Однако я бы хотел бы представить мою собственную интерпретацию фрактальных преобразований.
Я предлагаю рассмотреть базовое выражение фрактального преобразования PIFS:
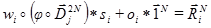
Данное выражение можно представить в виде следующей схемы:
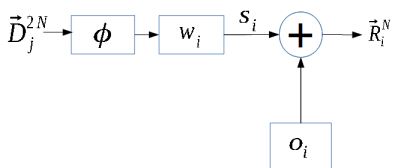
Учитывая тот факт, что указанное выражение описывает операции с векторами, рассмотрим схему операций над каждым элементом вектора:
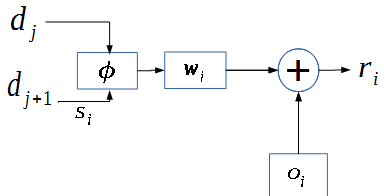
Я полагаю что многие читатели увидят схожесть данной схемы со схемой искусственного нейрона:
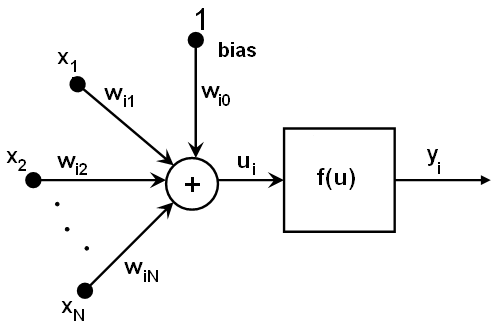
преобразования и
и 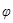 можно рассматривать как функцию сложения по входу,
можно рассматривать как функцию сложения по входу, 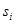 – чувствительность искусственного нейрона по входу,
– чувствительность искусственного нейрона по входу, 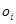 – уровень смещения — возбуждения искусственного нейрона. Внимательный читатель может указать, что чувствительность искусственного нейрона определяется для каждого входа, в то время как
– уровень смещения — возбуждения искусственного нейрона. Внимательный читатель может указать, что чувствительность искусственного нейрона определяется для каждого входа, в то время как 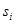 определяется как скаляр для всех входов. Также читатель укажет на необходимость на выходе функции для определения состояния искусственного нейрона в терминах Бинарной (Булевой) логики: активен или неактивен. Но являются ли такие требования важными? Допустимо ли, что бы чувствительность искусственного нейрона для всех входов была одинакова? Да, существуют алгоритмы обучения искусственных нейронных сетей с подобным правилом. Допустимо ли не бинарное значение на выходе искусственного нейрона? В начале развития теории искусственных нейронных сетей, когда схемы строились на транзисторах, конденсаторах и резисторах, и от них требовалось решать несложные задачи из области распознавания – к примеру распознавание почтовых индексов на почтовых конвертах и открытках с помощью перцептрона. Но с развитием нечёткой логики и открытием преимуществ «нечётких решений» (soft decisions) над «чёткими решениями» (hard decisions) необходимость подобной функции можно поставит под сомнение.
определяется как скаляр для всех входов. Также читатель укажет на необходимость на выходе функции для определения состояния искусственного нейрона в терминах Бинарной (Булевой) логики: активен или неактивен. Но являются ли такие требования важными? Допустимо ли, что бы чувствительность искусственного нейрона для всех входов была одинакова? Да, существуют алгоритмы обучения искусственных нейронных сетей с подобным правилом. Допустимо ли не бинарное значение на выходе искусственного нейрона? В начале развития теории искусственных нейронных сетей, когда схемы строились на транзисторах, конденсаторах и резисторах, и от них требовалось решать несложные задачи из области распознавания – к примеру распознавание почтовых индексов на почтовых конвертах и открытках с помощью перцептрона. Но с развитием нечёткой логики и открытием преимуществ «нечётких решений» (soft decisions) над «чёткими решениями» (hard decisions) необходимость подобной функции можно поставит под сомнение.
Что же получиться, если взглянуть на фрактальные преобразования с точки зрения теории искусственных нейронных сетей? Каждые элемент вектора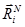 может быть рассмотрен как один искусственный нейрон. В этом случае векторе
может быть рассмотрен как один искусственный нейрон. В этом случае векторе 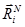 может быть рассмотрен как слой искусственных нейронов с общими свойствами. Однако, таких «слоёв» может быть несколько тысяч для небольшого изображения. Преобразование на плоскости
может быть рассмотрен как слой искусственных нейронов с общими свойствами. Однако, таких «слоёв» может быть несколько тысяч для небольшого изображения. Преобразование на плоскости  может быть интерпретировано как трассировка связей между искусственными нейронами. Искусственная нейронная сеть с трассировкой связей–топологии между слоями искусственных нейронов для каждой индивидуальной задачи – звучит весьма необычно, не так ли? Какими особенностями могут могут обладать подобные искусственные нейронные сети:
может быть интерпретировано как трассировка связей между искусственными нейронами. Искусственная нейронная сеть с трассировкой связей–топологии между слоями искусственных нейронов для каждой индивидуальной задачи – звучит весьма необычно, не так ли? Какими особенностями могут могут обладать подобные искусственные нейронные сети:
Как можно назвать подобную искусственную нейронную сеть – рекурсивная, масштабируемая, асинхронная, не детерминированная искусственная нейронная сеть с трассировкой топологии и «мягким» решением. Интересным фактом является то, что уже существует искусственная нейронная сеть с подобными свойствами — искусственная нейронная сеть Хопфилда. Эта искусственная нейронная сеть Хопфилда также рекурсивна, также сходиться к устойчивому состоянию и может быть асинхронна. Однако она включает один слой, не включает трассировку топологии и не формирует «мягкое» решение. Интересно то, что фрактальные преобразования, как и искусственная нейронная сеть Хопфилда обладают общими свойствами фильтрации – восстановления повреждённых образов (конечно, фрактальные преобразования могут работать с реальными изображениями):



Вы можете видеть, что после удаления нескольких элементов фрактальные преобразования могут построить изображение, близкое к исходному после одной итерации. Однако изображение «Роза», которое сильно отличается от оригинального создаёт, весьма хаотичное распределение интенсивности пикселей. Это вполне соответствует свойству фильтрации – восстановления повреждённых образов.
На этом можно закончить данную статью. Надеюсь, высказанные идеи обратят ваше внимание на экзотическую область фрактальных преобразований.
Чего вы не найдёте здесь:
- Сложных уравнений. Цель данной публикации является представление идей и видение задачи. И как любое видение оно во многом абстрактно;
- Каких либо генераторов фрактальных изображений. Такие изображения выглядят интересно, но мня интересуют реальные задачи.
Что вы найдёте здесь:
- Краткий обзор применения фрактальных преобразований к задаче сжатия данных с потерями;
- Необычная интерпретация фрактальных преобразований;
- Ссылки на реальный код компрессора и декомпрессора аудио данных посредством фрактальных преобразований (декомпрессор представлен в форме плагина для аудио плейера Winamp);
- Описание нового формата для хранения сжатых аудио данных с пятью уникальными свойствами, отличающими новый формат от многих хорошо известных индустриальных аудио форматов.
Думаю, что для большинства читателей этой публикации данная задача покажется странной. Обычно, понятие фрактала связывают с красивыми картинками — результатами выполнения фрактальных преобразований, именуемыми также фрактальными (или «странными») аттракторами. Однако, внимательное изучение фрактальных преобразований позволяет понять, что фракталы это не только красивые изображения. Фрактальные преобразования определяют проекции элементов в замкнутом множестве. Таким множествами могут быть цветные точки в 2.5 D пространстве, набор точек на 2 D плоскости, или набор дискретных выборок аудио потока в 1.5 D пространстве.
Я заинтересовался фрактальными преобразованиями с момента написания диссертации на соискания степени кандидата технических наук. Тема диссертации была — «Алгоритмы сокращения вычислительной сложности фрактального анализа в системах обработки визуальных данных». Диссертация была с успехом защищена и принята к публикации LAP LAMBERT Academic Publishing. Иногда встречаю ссылки на неё на сайтах Amazon и Ozon.
Я потратил много времени на изучение как теоретических основ, так и практических результатов исследований фрактальных преобразований и обнаружил только две попытки развития фрактальных преобразований до уровня индустриальных стандартов:
- Video codec — 'ClearVideo' by company Iterated System Incorporated.
- Image/video codec — 'FIASCO' by Ullrich Hafner.
Однако, данные попытки не привели к значительному успеху. Причиной провалов послужила значительная вычислительная сложность.
Математические основы
Построение изображений на основе фрактальных преобразований не представляет математической сложности. Известный фрактал (фрактальное множество) Манделброта строится исходя из следующего преобразования:
Z(n+1) = Zn^2 + C where n = 1, 2, 3,…

Таким образом, очень сложная визуализация может быть достигнута очень простым выражением. Это приводит к следующему вопросу — возможно ли построить реальное изображение посредством фрактального преобразования? Данный вопрос был разрешён утвердительно. Более точно, можно найти такое фрактальное преобразование, которое способно построить изображение с искажениями меньшем или равными любому предопределённому значению. Это означает, что сгенерированное изображение может отличаться от оригинального на величину, неотличимую зрителем благодаря избыточности визуальной информации изображения. Таким образом, фрактальное кодирование изображения является технологией обработки изображения с потерей качества.
В книге — Amazon или Ozon можно найти точное доказательства применимости фрактального преобразования к задачам обработки изображений – теорема «Коллажа» Майкла Брансли.
PIFS
Вы можете спросить – как выполнить фрактальное кодирование (или более точно – фрактальный анализ)? Визуализация фрактального множества Мандельброта весьма впечатляет, но оно было разработано после многих лет исследований. Попытка найти подходящее фрактальное преобразование путём простого перебора бесперспективна. Решение данной проблемы было предложено Майклом Брансли и его аспирантами (Майклом Брансли в дальнейшем основал Iterated Systems Incorporated). Они предложили блочную схему фрактального преобразования. С точки зрения выполнения фрактальных преобразований не существует различий в применимости фрактальных преобразований к множеству точек или к множеству блоков точек — partitioned iterated function systems (PIFS). Подобная схема базируется на извлечении копии точек из одной части множества точек, применении преобразований к копии и вставка результат в другую часть множества – это отличает данный подход от фрактальных преобразований для отдельных точек. PIFS схему можно представить в следующем виде:

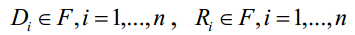
где F – оригинальное множество точек, D и R множества областей точек из F,
 — преобразование одной области из множества D и область множества R. Множества
— преобразование одной области из множества D и область множества R. Множества  и определяют искомые фрактальные преобразования. Важно отметить, что если фрактальное преобразование для фрактального множества Мандельброта базируется на одном уравнении фрактального преобразования и идеи глобального самоподобия (то есть подобие всего множества любой его части), то PIFS схема базируется на группе фрактальных преобразований и идеи локальном подобии отдельных областей множества.
и определяют искомые фрактальные преобразования. Важно отметить, что если фрактальное преобразование для фрактального множества Мандельброта базируется на одном уравнении фрактального преобразования и идеи глобального самоподобия (то есть подобие всего множества любой его части), то PIFS схема базируется на группе фрактальных преобразований и идеи локальном подобии отдельных областей множества. Вы можете спросить – как это относится к реальным изображениям? На реальных изображениях маловероятно найти глобальное самоподобие, но возможно установить подобие между разными областями реального изображения при условии допустимого отклонения. Если результирующий объём памяти для хранения системы уравнений фрактальных преобразований меньше объёма памяти для хранения оригинального изображения – то получается сжатие изображения с потерями. Данный подход обработки изображений отличается от классической идеи линейной интерполяции сигналов.
Для понимания данного различия требуется обратить внимание на три главных свойства фрактальных преобразований:
- фрактальное преобразование является рекурсивным – оно основано на идее неограниченного применении данного преобразования к множеству;
- фрактальное преобразование является сжимающим – это значит, результат всегда меньше оригинала;
- пространство фрактальное преобразование компактно – все преобразования над множеством отражается на само множество (самоподобие).
По аналогии с фрактальным преобразованием множества Манделброта, PIFS преобразование для реальных изображений можно представит в следующем виде:
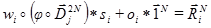
где
 – преобразование в пространстве точек изображения,
– преобразование в пространстве точек изображения, 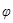 – сжимающее преобразование вектора с длинной
– сжимающее преобразование вектора с длинной 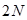 в вектор с длинной
в вектор с длинной 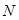 , но что означают переменные
, но что означают переменные 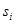 и
и 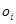 ? Переменные
? Переменные  и
и 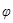 описывают преобразование на плоскости, но каждая точка реального изображения имеет специальное значение – интенсивность собственной яркости которая должна быть рассмотрена как часть пространства фрактального преобразования:
описывают преобразование на плоскости, но каждая точка реального изображения имеет специальное значение – интенсивность собственной яркости которая должна быть рассмотрена как часть пространства фрактального преобразования: 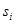 – сжимающее преобразование яркости и
– сжимающее преобразование яркости и 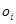 – смещение интенсивности яркости (по аналогии уравнении прямой – f(y) = y*s+o).
– смещение интенсивности яркости (по аналогии уравнении прямой – f(y) = y*s+o). Что делать с этом уравнением? Очень просто – выполнить данное выражение для всех групп преобразований (
 ,
, 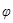 ,
, 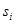 ,
, 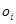 ) что должно заполнить множество R, заполняющее все изображение F. И ещё раз, и ещё раз (рекурсивное выполнение), до бесконечности. В реальности, всё намного проще – после каждого рекурсивного выполнения итерации синтеза фрактального множества расстояние между точками уменьшается (сжимающее свойство фрактального преобразования), но если для аналитического пространства нет ограничений в делимости, то для дискретного пространства цифровых изображений новые точки будут попадать в отсечённое пространство между соседними выборками. Это случится после
) что должно заполнить множество R, заполняющее все изображение F. И ещё раз, и ещё раз (рекурсивное выполнение), до бесконечности. В реальности, всё намного проще – после каждого рекурсивного выполнения итерации синтеза фрактального множества расстояние между точками уменьшается (сжимающее свойство фрактального преобразования), но если для аналитического пространства нет ограничений в делимости, то для дискретного пространства цифровых изображений новые точки будут попадать в отсечённое пространство между соседними выборками. Это случится после 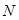 рекурсивных итераций PIFS.
рекурсивных итераций PIFS. Ожидаемый вопрос – как найти упомянутые коэффициенты
 ,
, 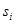 ,
, 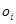 для системы фрактальных преобразований? Задача подобного поиска может быть автоматизирована исходя из следующего уравнения:
для системы фрактальных преобразований? Задача подобного поиска может быть автоматизирована исходя из следующего уравнения: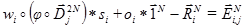
задача поиска заключается в поиске пары
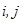 , которая минимизирует длину вектора отклонения
, которая минимизирует длину вектора отклонения 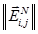 . Если установить экстремальное значение допустимого отклонения равное 0, то можно вывести следующие приближения для
. Если установить экстремальное значение допустимого отклонения равное 0, то можно вывести следующие приближения для 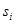 и
и 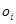 :
: 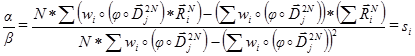
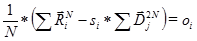
Данные выражения позволяют рассчитать оптимальные значения
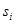 и
и 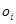 , но неизвестными переменными остаются
, но неизвестными переменными остаются  и пары
и пары 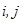 . К сожалению, на настоящий момент отсутствуют аналитические решения для этих переменных – остаётся только задавать множества
. К сожалению, на настоящий момент отсутствуют аналитические решения для этих переменных – остаётся только задавать множества  и пар
и пар 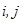 , и перебирать их комбинации для минимизации
, и перебирать их комбинации для минимизации 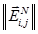 уравнения:
уравнения: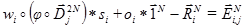
Для эффективной минимизации требуется задавать большие диапазоны значений множества
 и пар
и пар 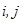 , что ведёт к «комбинаторному взрыву» – необходимости к перебору сотен тысяч всевозможных комбинаций, на что требуется часы работы компьютерного процессора. Именно эта проблема и не позволяет перейти фрактальному анализу изображений из области экзотических исследований в сферу индустриальных стандартов.
, что ведёт к «комбинаторному взрыву» – необходимости к перебору сотен тысяч всевозможных комбинаций, на что требуется часы работы компьютерного процессора. Именно эта проблема и не позволяет перейти фрактальному анализу изображений из области экзотических исследований в сферу индустриальных стандартов.Аудио
Предвижу вопрос – всё выше описанное интересно, но причём тут звук и сжатие звуковых данных? Я полагаю многие уже поняли, что для фрактального анализа природа множеств не имеет значения – множество пикселей на плоскости или множество выборок из звукового потока. Если накапливать выборки входного звукового потока в буфере и затем обрабатывать их как отдельные множества, то можно сформировать систем фрактальных преобразований, из которых можно синтезировать фрактальные множества, приближённые к оригинальным выборкам звукового потока. Что и было реализованно в моём проекте, который включает кодер ROAD и декодер (в форме плагина для Winamp) — тестовые аудио файлы: Origa — Inner Universe 4Samples.road.wav и Alpha — Revolution in Paradise 4Samples.road.wav. Новый алгоритм сжатия звуковых данных позволил разработать формат с пятью уникальными свойствами:
- Предпрослушивание. Данный термин звучит странно, но я решил использовать его по аналогии с термином «Предпросмотр» из описания формата сжатия изображения JPEG2000. Но что это может значить для аудио файла? Если взглянуть на выражение для расчёта коэффициента
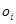 , то можно увидеть что оно рассчитывается на основе усреднения значений соседних выборок. В результате, через подстановку можно получить следующее выражение:
, то можно увидеть что оно рассчитывается на основе усреднения значений соседних выборок. В результате, через подстановку можно получить следующее выражение:
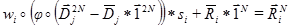
Это выражение показывает важный факт – часть коэффициентов фрактальных преобразований можно рассматривать как усреднённое значение пикселей изображения или выборок звукового потока. Это значение является «точкой роста» фрактального множества. Фрактальные преобразования нуждаются в подобных точках. Однако, при использовании PIFS для анализа звуковых данных можно ограничить размеры областей в 4 точки–выборки – это позволяет получить усреднённый звуковой поток в низкочастотной области (к примеру для оригинальной частоты звукового потока в 48000 Гц, усреднённый поток имеет частоту в 12000 Гц). В результате, сжатый поток можно прослушать с ухудшенным качеством без декодирования. Полагаю что данное свойство можно определить как «Предпрослушивание».
- Частичная совместимость. Из возможности организации отдельного низкочастотного потока звуковых данных из коэффициентов фрактальных преобразований возникает вопрос – как это реализовать? Можно резервировать отдельный участок потока данных, но факт что данный поток является несжатым потоком данных, приводит к идее, что данный поток может быть дополнительно сжат другим алгоритмом и упакован в известный индустриальный формат. В этом случае файл может быть воспроизведён в аудио проигрывателе, совместимым с индустриальным форматом с ухудшенным качеством. Данную идею можно реализовать в форме стека компрессоров. В моём проекте был выбран формат WAVE от Майкрософт. Этот формат не включает сжатие, но позволяет на практике реализовать стек форматов и частичную совместимость:
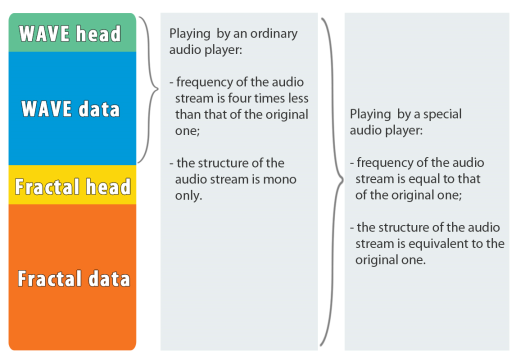
- Разгон. Идея данного свойства заключается в увеличении частоты декодированного аудио потока. Понять идею реализации данного свойства можно если рассмотреть почему данное свойство невозможно реализовать во многих индустриальных форматах. К примеру рассмотри формат mp3 – при попытке удвоения частоты декодированного аудио потока требуется увеличить базис обратного дискретно-косинусного преобразования с 128 до 256, но сжатые данные включают данные только для 128. Это приводит к проблеме неполноты базиса ортогонального преобразования. Подобная проблема возникает и с форматами на основе линейного предсказания. Однако, для фрактального анализа дело обстоит иначе. Рассмотренные ранее коэффициенты
 ,
, 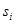 ,
, 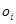 не связаны с размером базиса преобразования:
не связаны с размером базиса преобразования: 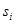 и
и 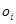 – скаляры интенсивности,
– скаляры интенсивности,  – преобразование в пространстве – смещение, отражение и т.п… Близкой аналогией являются растровые и векторные форматы изображений: если в растровых форматах предполагается наличие одного аппроксимирующего базиса и исследуется его реакция на дискретное изображение, то в векторных форматах изображение синтезируется из системы уравнений. По аналогии, большинство индустриальных форматов сжатия звуковых данных исследуют реакцию аппроксимирующего базиса на входные звуковые данные и при декодировании восстанавливают звуковые данные по реакции из принципа обратимости аппроксимирующего базиса с конечной импульсной характеристикой. В тоже время, как фрактальный аппроксимирующий базис является рекурсивным с бесконечной импульсной характеристикой, синтезирующий результирующее фрактальное множество. Это важное отличие – коэффициенты
– преобразование в пространстве – смещение, отражение и т.п… Близкой аналогией являются растровые и векторные форматы изображений: если в растровых форматах предполагается наличие одного аппроксимирующего базиса и исследуется его реакция на дискретное изображение, то в векторных форматах изображение синтезируется из системы уравнений. По аналогии, большинство индустриальных форматов сжатия звуковых данных исследуют реакцию аппроксимирующего базиса на входные звуковые данные и при декодировании восстанавливают звуковые данные по реакции из принципа обратимости аппроксимирующего базиса с конечной импульсной характеристикой. В тоже время, как фрактальный аппроксимирующий базис является рекурсивным с бесконечной импульсной характеристикой, синтезирующий результирующее фрактальное множество. Это важное отличие – коэффициенты  ,
, 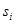 ,
, 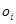 определяют уравнения PIFS. В результате, возможно выбирать размер базиса и синтезировать больше выборок звукового потока в единицу времени чем было в оригинальном звуковом потоке. Подобный результат можно наблюдать при масштабировании векторных форматов изображений. Данное свойство реализовано в плагине для Winamp.
определяют уравнения PIFS. В результате, возможно выбирать размер базиса и синтезировать больше выборок звукового потока в единицу времени чем было в оригинальном звуковом потоке. Подобный результат можно наблюдать при масштабировании векторных форматов изображений. Данное свойство реализовано в плагине для Winamp.

- Расширение динамического диапазона. Это логичное продолжение свойства увеличения частоты декодированного звукового потока – при увеличении разрядности потока с 16 бит до 32 бит новые выборки звукового потока будут синтезированы в расширенном диапазоне.
- Недетерминированное декодирование. Система PIFS предполагает множество фрактальных преобразований устанавливающих локальные подобия. Исходя из ранее рассмотренных выражений можно сделать вывод, что каждое из множества фрактальных преобразований может быть выполнено независимо, но возникает вопрос – в каком порядке их следует выполнять? Логично выполнять в порядке, в котором был проведён фрактальный анализ, но данное заключение ошибочно – каждое фрактальное преобразование эквивалентно любому другому из множества. Данная идея выражена в реализации выбора очередного фрактального преобразования генератором случайных чисел. Для большинства индустриальных форматов обратимость алгоритмов сжатия является главным требованием, но фрактальные преобразования избавлены от подобного условия.
Интерпретация
Многие математические концепции имеют физические интерпретации. К примеру –
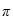 и окружность круга или натуральный логарифм и спиральная раковина моллюска. Часто указывают на связь фрактальных множеств с ростом кристалов или деревьев. Однако я бы хотел бы представить мою собственную интерпретацию фрактальных преобразований.
и окружность круга или натуральный логарифм и спиральная раковина моллюска. Часто указывают на связь фрактальных множеств с ростом кристалов или деревьев. Однако я бы хотел бы представить мою собственную интерпретацию фрактальных преобразований. Я предлагаю рассмотреть базовое выражение фрактального преобразования PIFS:
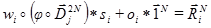
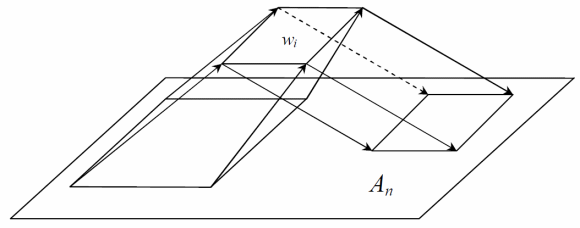
Данное выражение можно представить в виде следующей схемы:

Учитывая тот факт, что указанное выражение описывает операции с векторами, рассмотрим схему операций над каждым элементом вектора:

Я полагаю что многие читатели увидят схожесть данной схемы со схемой искусственного нейрона:

преобразования
 и
и 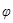 можно рассматривать как функцию сложения по входу,
можно рассматривать как функцию сложения по входу, 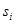 – чувствительность искусственного нейрона по входу,
– чувствительность искусственного нейрона по входу, 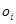 – уровень смещения — возбуждения искусственного нейрона. Внимательный читатель может указать, что чувствительность искусственного нейрона определяется для каждого входа, в то время как
– уровень смещения — возбуждения искусственного нейрона. Внимательный читатель может указать, что чувствительность искусственного нейрона определяется для каждого входа, в то время как 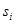 определяется как скаляр для всех входов. Также читатель укажет на необходимость на выходе функции для определения состояния искусственного нейрона в терминах Бинарной (Булевой) логики: активен или неактивен. Но являются ли такие требования важными? Допустимо ли, что бы чувствительность искусственного нейрона для всех входов была одинакова? Да, существуют алгоритмы обучения искусственных нейронных сетей с подобным правилом. Допустимо ли не бинарное значение на выходе искусственного нейрона? В начале развития теории искусственных нейронных сетей, когда схемы строились на транзисторах, конденсаторах и резисторах, и от них требовалось решать несложные задачи из области распознавания – к примеру распознавание почтовых индексов на почтовых конвертах и открытках с помощью перцептрона. Но с развитием нечёткой логики и открытием преимуществ «нечётких решений» (soft decisions) над «чёткими решениями» (hard decisions) необходимость подобной функции можно поставит под сомнение.
определяется как скаляр для всех входов. Также читатель укажет на необходимость на выходе функции для определения состояния искусственного нейрона в терминах Бинарной (Булевой) логики: активен или неактивен. Но являются ли такие требования важными? Допустимо ли, что бы чувствительность искусственного нейрона для всех входов была одинакова? Да, существуют алгоритмы обучения искусственных нейронных сетей с подобным правилом. Допустимо ли не бинарное значение на выходе искусственного нейрона? В начале развития теории искусственных нейронных сетей, когда схемы строились на транзисторах, конденсаторах и резисторах, и от них требовалось решать несложные задачи из области распознавания – к примеру распознавание почтовых индексов на почтовых конвертах и открытках с помощью перцептрона. Но с развитием нечёткой логики и открытием преимуществ «нечётких решений» (soft decisions) над «чёткими решениями» (hard decisions) необходимость подобной функции можно поставит под сомнение. Что же получиться, если взглянуть на фрактальные преобразования с точки зрения теории искусственных нейронных сетей? Каждые элемент вектора
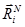 может быть рассмотрен как один искусственный нейрон. В этом случае векторе
может быть рассмотрен как один искусственный нейрон. В этом случае векторе 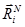 может быть рассмотрен как слой искусственных нейронов с общими свойствами. Однако, таких «слоёв» может быть несколько тысяч для небольшого изображения. Преобразование на плоскости
может быть рассмотрен как слой искусственных нейронов с общими свойствами. Однако, таких «слоёв» может быть несколько тысяч для небольшого изображения. Преобразование на плоскости  может быть интерпретировано как трассировка связей между искусственными нейронами. Искусственная нейронная сеть с трассировкой связей–топологии между слоями искусственных нейронов для каждой индивидуальной задачи – звучит весьма необычно, не так ли? Какими особенностями могут могут обладать подобные искусственные нейронные сети:
может быть интерпретировано как трассировка связей между искусственными нейронами. Искусственная нейронная сеть с трассировкой связей–топологии между слоями искусственных нейронов для каждой индивидуальной задачи – звучит весьма необычно, не так ли? Какими особенностями могут могут обладать подобные искусственные нейронные сети:- Рекурсивность – результат работы искусственной нейронной сети становится входными данными для неё самой до установления равновесного состояния – называемого для фрактальных преобразований «аттрактором».
- Спиральная топология – условие локального самоподобия.
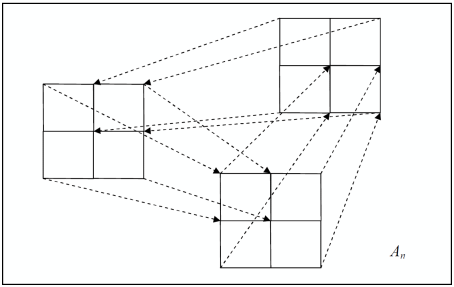
- Случайный выбор последовательности выполнения преобразований — слоёв.
- Предпрослушивание – возможность установки исходного уровня искусственной нейронной сети из реального источника: изображение или звук низкого качества.
- Разгон – простое масштабирование существующей искусственной нейронной сети путём добавления или удаления искусственных нейронов из каждого слоя без необходимости пересчёта конфигурации искусственной нейронной сети. Это позволяет создавать более детальное состояние сети с генерацией новых деталей.
Как можно назвать подобную искусственную нейронную сеть – рекурсивная, масштабируемая, асинхронная, не детерминированная искусственная нейронная сеть с трассировкой топологии и «мягким» решением. Интересным фактом является то, что уже существует искусственная нейронная сеть с подобными свойствами — искусственная нейронная сеть Хопфилда. Эта искусственная нейронная сеть Хопфилда также рекурсивна, также сходиться к устойчивому состоянию и может быть асинхронна. Однако она включает один слой, не включает трассировку топологии и не формирует «мягкое» решение. Интересно то, что фрактальные преобразования, как и искусственная нейронная сеть Хопфилда обладают общими свойствами фильтрации – восстановления повреждённых образов (конечно, фрактальные преобразования могут работать с реальными изображениями):



Вы можете видеть, что после удаления нескольких элементов фрактальные преобразования могут построить изображение, близкое к исходному после одной итерации. Однако изображение «Роза», которое сильно отличается от оригинального создаёт, весьма хаотичное распределение интенсивности пикселей. Это вполне соответствует свойству фильтрации – восстановления повреждённых образов.
Заключение
На этом можно закончить данную статью. Надеюсь, высказанные идеи обратят ваше внимание на экзотическую область фрактальных преобразований.
