Инвариант дистанции (квадрат расстояния) между элементами можно обобщить, если умножать разность элементов не на саму себя, а на другую разность элементов. Полученное значение будет отражать скалярное произведение упорядоченных пар.

Координаты вектора могут быть получены на как разность координат элементов, но обратное неверное — по координатам вектора невозможно восстановить координаты образовавших его элементов. Координаты двух элементов несут в себе больше информации, чем координаты вектора. Поэтому из элементов можно образовать пару — улучшенный аналог вектора. Такой набор из двух элементов называют упорядоченной парой.
Каждой упорядоченной паре можно сопоставить вектор — разность элементов, образующих пару. Для двух векторов можно определить скалярное произведение, которое можно также рассматривать как характеристику четырех элементов пространства.
Для уменьшения громоздкости в данной части будем обозначать элементы строчными символами. Пара — это совокупность двух элементов: . Вектор, соответствующий паре, — это разность элементов пары:
. Вектор, соответствующий паре, — это разность элементов пары:

Норма элемента — это его скалярное произведение с самим собой:

Это же определение можно использовать для вектора пары, которая, как известно, отражает квадрат расстояния между элементами пары:

Если заданы две разных пары и
и  , то можно определить скалярное произведение между соответствующими векторами:
, то можно определить скалярное произведение между соответствующими векторами:

Индексы задают одну пару, а индексы
задают одну пару, а индексы  — другую.
— другую.
Выражение (3.4) определяет скаляр, зависящий от взаимного положения 4-х элементов. Важно, что данный скаляр может быть выражен через расстояния между элементами .
.
Как известно, расстояние между элементами связано со скалярным произведением между ними:
 .
.
Раскрывая произведение (3.4) с учетом (3.5), получаем:

Это общая формула скалярного произведения пар. Порядок индексов важен — задает пары и направление соответствующих им векторов.
Выражения, подобные (3.6), часто возникают в разных местах математики. Связано это с общностью вывода данной формулы. Отметим, что мы использовали только самые общие свойства алгебраического выражения. Поэтому в качестве элементов могут использоваться любые объекты, для которых определена операция произведения. Тождество будет справедливо и для них, в общей форме оно выглядит так:

Если пары имеют общую вершину , то формула (3.6) упрощается:
, то формула (3.6) упрощается:


Формула (3.7) — это теорема косинусов для треугольника. Здесь пары, между которыми определена взаимная норма, имеют общий элемент k — смежные пары.
На 3-х вершинах можно определить три скалярных произведения. Их сумма выражается через сумму дистанций между вершинами:

Квадрат скалярного произведения на 3-х вершинах связан с площадью образуемого ими треугольника (формула Герона):
(формула Герона):

В общем случае вершины пар могут не лежать в одной плоскости, поэтому данному определению скалярного произведения не всегда можно сопоставить косинус угла между направлениями.
Перечислим свойства скалярного произведения (3.6).
1) Не зависит от перестановки пар:

2) Антисимметрично относительно перестановки элементов в паре или
или  :
:

3) Для 4-х элементов существует только два независимых скалярных произведения пар ввиду тождества:

Математики увидят в формуле (3.9.3) первое тождество Бьянки. Из чего можно сделать вывод, что структуры тензора кривизны (Римана) и скалярного произведения пар — подобны.
4) Норма независимых пар может быть выражена через разность норм смежных пар:

Этим тождеством воспользуемся в следующей статье.
5) Дистанция между элементами и
и  может быть выражена через значения скалярных произведений смежных и независимых пар:
может быть выражена через значения скалярных произведений смежных и независимых пар:

В качестве элементов, образующих пару, могут быть выбраны вершины базиса. Тогда скалярное произведение пар становится тензором — набором скалярных произведений между всеми возможными парами элементов данного базиса. Чтобы отличать тензоры от скаляров будем использовать для первых заглавные буквы. То есть вместо скаляра для элементов базиса получаем тензор
для элементов базиса получаем тензор  .
.
Скалярное произведение пар, образованных элементами базиса, может быть выражено через свойства лапласиана базиса.
Если заданы две пары вершин и
и  , то значение их скалярного произведения можно получить делением кофактора 2-го порядка
, то значение их скалярного произведения можно получить делением кофактора 2-го порядка  на скалярный потенциал лапласиана
на скалярный потенциал лапласиана  :
:

Кофактором называется определитель минора квадратной матрицы (с учетом знака). Скалярный потенциал
называется определитель минора квадратной матрицы (с учетом знака). Скалярный потенциал  — это кофактор 1-го порядка от лапласиана (см. (1.12) из первой статьи).
— это кофактор 1-го порядка от лапласиана (см. (1.12) из первой статьи).
Таким образом необходимо из матрицы лапласиана удалить столбцы, соответствующие одному вектору (в формуле это -й столбцы), и строки, соответствующие другому (
-й столбцы), и строки, соответствующие другому ( ), после чего разделить определитель получившегося минора на скалярный потенциал
), после чего разделить определитель получившегося минора на скалярный потенциал  . Если удаляемые столбцы и строки лапласиана — одни и те же, то получим значение дистанции между узлами.
. Если удаляемые столбцы и строки лапласиана — одни и те же, то получим значение дистанции между узлами.
Между любыми парами вершин графа можно определить их взаимную норму — скалярное произведение. Поскольку граф обычно задан лапласианом, то для расчета можно использовать формулу (3.10.1).

Пусть, например, в качестве образующих вершин двух пар выбраны — и
и  . Тогда скалярное произведение между данными парами дается формулой (3.6):
. Тогда скалярное произведение между данными парами дается формулой (3.6):

Для графа, представляющего собой электрическую цепь, значение скалярного произведения отражает понятие обобщенного сопротивления в электрической цепи. Для измерения такого («кажущегося») сопротивления источник тока (напряжение) прикладывается к одним узлам (A и B), а разность потенциалов измеряется между другими (M и N). Взаимная норма (скалярное произведение) пар равна нулю, если внешняя разность потенциалов не приводит к разности потенциалов на измеряемой паре.
Граф не обязательно должен быть дискретным,- грунт является примером сплошного (непрерывного) графа, на котором можно проводить измерения скалярного произведения между выбранными элементами.
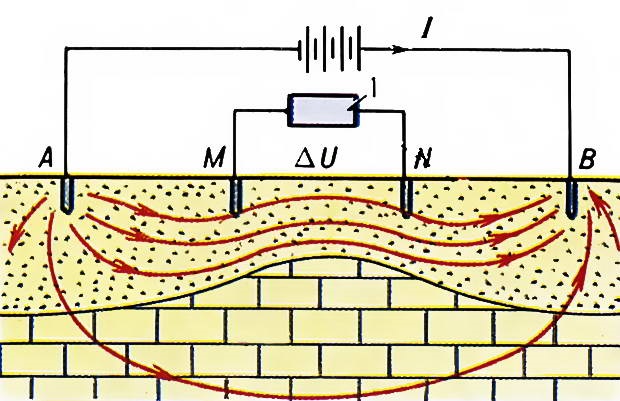
Схема установки для исследования методом сопротивления: A и B – питающие заземления; M и N – измерительные заземления; 1 – измерительный прибор (из книги «Электроразведка», Якубовский Ю. B., M., 1980).
На рисунке показана схема измерения скалярного произведения пар и
и  на грунте.
на грунте.
В следующей статье разберем подробнее, почему отношение заданной и измеряемой разностей потенциалов узлов оказалось связанным со скалярным произведением пар.
Подматрицу значений взаимных норм (скалярных произведений) пар можно получить обращением минора лапласиана. Обозначим лапласиан, из которого удалены -я строка и
-я строка и  -й столбец, как
-й столбец, как  . Тогда имеет место тождество:
. Тогда имеет место тождество:

Отметим, что в матрице отсутствуют
отсутствуют  -я строка и
-я строка и  -й столбец.
-й столбец.
Если известна матрица скалярных произведений пар , то можно восстановить дистанционную матрицу
, то можно восстановить дистанционную матрицу  на основании преобразования дистанции. Вначале расширяем подматрицу
на основании преобразования дистанции. Вначале расширяем подматрицу  отсутствующей строкой
отсутствующей строкой  и столбцом
и столбцом  с нулевыми значениями. К полученной матрице применяем преобразование дистанции:
с нулевыми значениями. К полученной матрице применяем преобразование дистанции:

которое в нашем случае принимает вид тождества (3.9.5):

Совокупность формул (3.10.2) и (3.10.3) — один из способов получить дистанционную матрицу по заданному лапласиану. Удаляем из лапласиана какой-либо из узлов (пусть будет ) и обращаем. Получаем матрицу скалярных произведений пар
) и обращаем. Получаем матрицу скалярных произведений пар  (ее другое название — фундаментальная матрица, см. следующую часть). Значение индекса
(ее другое название — фундаментальная матрица, см. следующую часть). Значение индекса  фиксировано — базовая вершина. В матрице
фиксировано — базовая вершина. В матрице  первая вершина пар находится в базовом узле
первая вершина пар находится в базовом узле  , а вторая пробегает по остальным вершинам базиса.
, а вторая пробегает по остальным вершинам базиса.
Далее применяем к матрице преобразование дистанции (3.10.3).
преобразование дистанции (3.10.3).
Если в графе изменить значение проводимости ребра (элемент лапласиана), то очевидно, что изменятся и все дистанции между вершинами (нормы векторов) . При увеличении проводимости дистанции должны сократиться (уменьшиться). Подарок богов в том, что можно оценить изменение дистанций не только качественно, но и количественно. Обозначим производную матрицы дистанций по лапласиану как
. При увеличении проводимости дистанции должны сократиться (уменьшиться). Подарок богов в том, что можно оценить изменение дистанций не только качественно, но и количественно. Обозначим производную матрицы дистанций по лапласиану как

Тензор — это матрица Якоби, то есть выражение изменений значений дистанционной матрицы
— это матрица Якоби, то есть выражение изменений значений дистанционной матрицы  при изменении значений лапласиана
при изменении значений лапласиана  . Оказывается, что данный тензор выражается через квадрат скалярного произведения пар:
. Оказывается, что данный тензор выражается через квадрат скалярного произведения пар:

То есть изменение величины связи узлов приводит к изменению дистанции между узлами
приводит к изменению дистанции между узлами  пропорционально величине скалярного произведения пар
пропорционально величине скалярного произведения пар  и
и  .
.
Тензор квадратов скалярного произведения обратим. Представим выражение (3.11) в следующем эквивалентном виде:
обратим. Представим выражение (3.11) в следующем эквивалентном виде:

Данную формулу можно трактовать как отклик на воздействие
на воздействие  . Тензор
. Тензор  играет роль передаточной функции (реакции на воздействие).
играет роль передаточной функции (реакции на воздействие).
Возможна и обратная ситуация, при которой воздействие и отклик меняются местами. Прямая и обратная передаточные функции связаны соотношением:
передаточные функции связаны соотношением:

Снова удача — тензор можно выразить через лапласиан:
можно выразить через лапласиан:

Значения тензора назовем квадросвязностью.
назовем квадросвязностью.
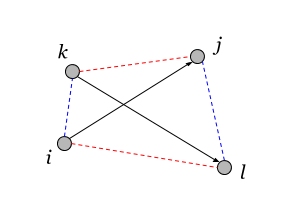
Значения тензора определены через значения лапласиана для 4-х вершин. Будем считать данные вершины вершинами графа. Допустим, что все 4 вершины различны:
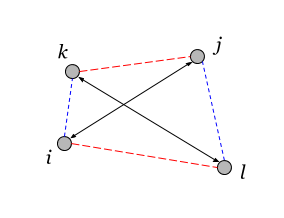
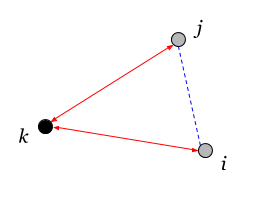
Здесь векторами обозначены пары вершин, между которыми считается квадросвязность. Пары имеют отличную от нуля квадросвязность только тогда, когда их вершины попарно связаны (необходимые связи показаны на рисунке одинаковым цветом). Если все связи в графе положительны, то квадросвязность между разными вершинами также всегда больше или равна нулю.
Если пары имеют общую вершину, то смысл квадросвязности меняется. Это связано с тем, что диагональные элементы лапласиана не равны нулю (как в дистанционной матрице), а отражают общую связность (проводимость) узла.

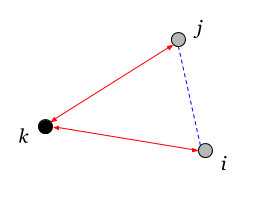
Пары вершин могут совпадать — диагональные элементы тензора квадросвязности.

Здесь характеризует связь двух узлов i и j. Считается как сумма произведения их суммарной проводимости (степени вершины)
характеризует связь двух узлов i и j. Считается как сумма произведения их суммарной проводимости (степени вершины)  и квадрата связи между узлами
и квадрата связи между узлами  .
.
Несмотря на то, что формально для тензора могут вычисляться элементы вида
могут вычисляться элементы вида  (одна из пар вырождена), данные (вырожденные) элементы являются линейно-зависимыми от остальных. Могут быть вычислены через сумму тензора по одному из индексов пары:
(одна из пар вырождена), данные (вырожденные) элементы являются линейно-зависимыми от остальных. Могут быть вычислены через сумму тензора по одному из индексов пары:

___
Подведем итоги. Рассмотрено полезное во всех отношениях понятие скалярного произведения пар элементов. В следующей статье поработаем с подпространством графа — что это такое, и каковы его свойства.
Оглавление
1. Симплексы и графы
2. Определение ди- и би-координат
3. Скалярное произведение пар
4. Пространство графа
5. Преобразование базиса
6. Граф-звезда
2. Определение ди- и би-координат
3. Скалярное произведение пар
4. Пространство графа
5. Преобразование базиса
6. Граф-звезда

Упорядоченная пара
Координаты вектора могут быть получены на как разность координат элементов, но обратное неверное — по координатам вектора невозможно восстановить координаты образовавших его элементов. Координаты двух элементов несут в себе больше информации, чем координаты вектора. Поэтому из элементов можно образовать пару — улучшенный аналог вектора. Такой набор из двух элементов называют упорядоченной парой.
Каждой упорядоченной паре можно сопоставить вектор — разность элементов, образующих пару. Для двух векторов можно определить скалярное произведение, которое можно также рассматривать как характеристику четырех элементов пространства.
Скалярное произведение
Для уменьшения громоздкости в данной части будем обозначать элементы строчными символами. Пара — это совокупность двух элементов:
Норма элемента — это его скалярное произведение с самим собой:
Это же определение можно использовать для вектора пары, которая, как известно, отражает квадрат расстояния между элементами пары:
Если заданы две разных пары
Индексы
Выражение (3.4) определяет скаляр, зависящий от взаимного положения 4-х элементов. Важно, что данный скаляр может быть выражен через расстояния между элементами
Как известно, расстояние между элементами связано со скалярным произведением между ними:
Раскрывая произведение (3.4) с учетом (3.5), получаем:
Это общая формула скалярного произведения пар. Порядок индексов важен — задает пары и направление соответствующих им векторов.
Выражения, подобные (3.6), часто возникают в разных местах математики. Связано это с общностью вывода данной формулы. Отметим, что мы использовали только самые общие свойства алгебраического выражения. Поэтому в качестве элементов могут использоваться любые объекты, для которых определена операция произведения. Тождество будет справедливо и для них, в общей форме оно выглядит так:
Пары с общей вершиной — смежные пары
Если пары имеют общую вершину
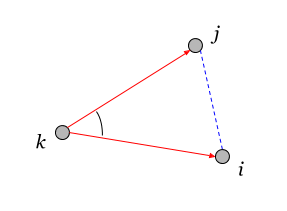
Формула (3.7) — это теорема косинусов для треугольника. Здесь пары, между которыми определена взаимная норма, имеют общий элемент k — смежные пары.
На 3-х вершинах можно определить три скалярных произведения. Их сумма выражается через сумму дистанций между вершинами:
Квадрат скалярного произведения на 3-х вершинах связан с площадью образуемого ими треугольника
Независимые пары — четыре разных вершины
В общем случае вершины пар могут не лежать в одной плоскости, поэтому данному определению скалярного произведения не всегда можно сопоставить косинус угла между направлениями.
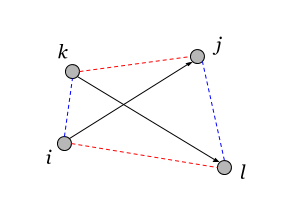
Перечислим свойства скалярного произведения (3.6).
1) Не зависит от перестановки пар:
2) Антисимметрично относительно перестановки элементов в паре
3) Для 4-х элементов существует только два независимых скалярных произведения пар ввиду тождества:
Математики увидят в формуле (3.9.3) первое тождество Бьянки. Из чего можно сделать вывод, что структуры тензора кривизны (Римана) и скалярного произведения пар — подобны.
4) Норма независимых пар может быть выражена через разность норм смежных пар:
Этим тождеством воспользуемся в следующей статье.
5) Дистанция между элементами
Пары на элементах базиса
В качестве элементов, образующих пару, могут быть выбраны вершины базиса. Тогда скалярное произведение пар становится тензором — набором скалярных произведений между всеми возможными парами элементов данного базиса. Чтобы отличать тензоры от скаляров будем использовать для первых заглавные буквы. То есть вместо скаляра
Скалярное произведение и кофакторы лапласиана
Скалярное произведение пар, образованных элементами базиса, может быть выражено через свойства лапласиана базиса.
Если заданы две пары вершин
Кофактором
Таким образом необходимо из матрицы лапласиана удалить столбцы, соответствующие одному вектору (в формуле это
Скалярное произведение пар на графе
Между любыми парами вершин графа можно определить их взаимную норму — скалярное произведение. Поскольку граф обычно задан лапласианом, то для расчета можно использовать формулу (3.10.1).
Пусть, например, в качестве образующих вершин двух пар выбраны —
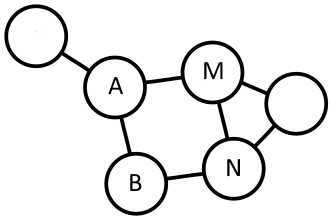
Для графа, представляющего собой электрическую цепь, значение скалярного произведения отражает понятие обобщенного сопротивления в электрической цепи. Для измерения такого («кажущегося») сопротивления источник тока (напряжение) прикладывается к одним узлам (A и B), а разность потенциалов измеряется между другими (M и N). Взаимная норма (скалярное произведение) пар равна нулю, если внешняя разность потенциалов не приводит к разности потенциалов на измеряемой паре.
Граф не обязательно должен быть дискретным,- грунт является примером сплошного (непрерывного) графа, на котором можно проводить измерения скалярного произведения между выбранными элементами.

Схема установки для исследования методом сопротивления: A и B – питающие заземления; M и N – измерительные заземления; 1 – измерительный прибор (из книги «Электроразведка», Якубовский Ю. B., M., 1980).
На рисунке показана схема измерения скалярного произведения пар
В следующей статье разберем подробнее, почему отношение заданной и измеряемой разностей потенциалов узлов оказалось связанным со скалярным произведением пар.
Обращение минора лапласиана
Подматрицу значений взаимных норм (скалярных произведений) пар можно получить обращением минора лапласиана. Обозначим лапласиан, из которого удалены
Отметим, что в матрице
Если известна матрица скалярных произведений пар
которое в нашем случае принимает вид тождества (3.9.5):
Совокупность формул (3.10.2) и (3.10.3) — один из способов получить дистанционную матрицу по заданному лапласиану. Удаляем из лапласиана какой-либо из узлов (пусть будет
Далее применяем к матрице
Квадрат скалярного произведения, матрица Якоби
Если в графе изменить значение проводимости ребра (элемент лапласиана), то очевидно, что изменятся и все дистанции между вершинами (нормы векторов)
Тензор
То есть изменение величины связи узлов
Тензор квадросвязности вершин
Тензор квадратов скалярного произведения
Данную формулу можно трактовать как отклик
Возможна и обратная ситуация, при которой воздействие и отклик меняются местами. Прямая и обратная
Снова удача — тензор
Значения тензора
Свойства тензора квадросвязности
Значения тензора определены через значения лапласиана для 4-х вершин. Будем считать данные вершины вершинами графа. Допустим, что все 4 вершины различны:
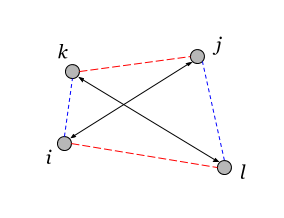
Здесь векторами обозначены пары вершин, между которыми считается квадросвязность. Пары имеют отличную от нуля квадросвязность только тогда, когда их вершины попарно связаны (необходимые связи показаны на рисунке одинаковым цветом). Если все связи в графе положительны, то квадросвязность между разными вершинами также всегда больше или равна нулю.
Если пары имеют общую вершину, то смысл квадросвязности меняется. Это связано с тем, что диагональные элементы лапласиана не равны нулю (как в дистанционной матрице), а отражают общую связность (проводимость) узла.
Пары вершин могут совпадать — диагональные элементы тензора квадросвязности.
Здесь
Несмотря на то, что формально для тензора
___
Подведем итоги. Рассмотрено полезное во всех отношениях понятие скалярного произведения пар элементов. В следующей статье поработаем с подпространством графа — что это такое, и каковы его свойства.