При написании статьи о разработке детектора аномалий я реализовывал один из алгоритмов, который называется "Инкрементальный растущий нейронный газ".
В советской литературе российском сегменте Интернета эта тема освещена достаточно слабо, и нашлась только одна статья, да и то с прикладным применением данного алгоритма.
Итак, что же такое — алгоритм инкрементального растущего нейронного газа?
Введение
IGNG, как и GNG, является адаптивным алгоритмом кластеризации.
Сам алгоритм описан в статье Прудента и Еннаджи за 2005-й год.
Также как и в GNG, существует множество векторов данных , либо генерирующая функция
, которая предоставляет вектора из произвольно распределённых данных (параметр
— время, либо номер сэмпла в выборке).
Дополнительных ограничений на данные алгоритм не накладывает.
Зато, внутри сильно отличается от GNG.
Данный алгоритм также любопытен ещё и тем, что он чуть точнее, чем GNG моделирует нейрогенез.
Описание алгоритма
Алгоритм разбивает множество данных на кластеры.
По сравнению с GNG, его преимуществом является более высокая скорость сходимости.
Идеи, на которых основан алгоритм:
- Теория адаптивного резонанса: сначала ищется ближайший нейрон, и если разница не превышает порога ("параметра бдительности"), производится корректировка весов или, иначе, изменение координаты нейрона в пространстве данных. Если порог не был преодолен, создаются новые нейроны, лучше приближающие значение сэмпла данных.
- Как связи, так и нейроны имеют параметр возраст (у GNG — только связи), который сначала равен нулю, но увеличивается по мере обучения.
- Нейрон появляется не сразу: сначала появляется эмбрион (или зародышевый нейрон), возраст которого увеличивается с каждой итерацией, пока он не созреет. После обучения, в классификации принимают участие только зрелые нейроны.
Основной цикл
Работа начинается с пустого графа. Параметр инициализируется среднеквадратическим отклонением по обучающей выборке:
Где: — среднее между координатами по выборке.
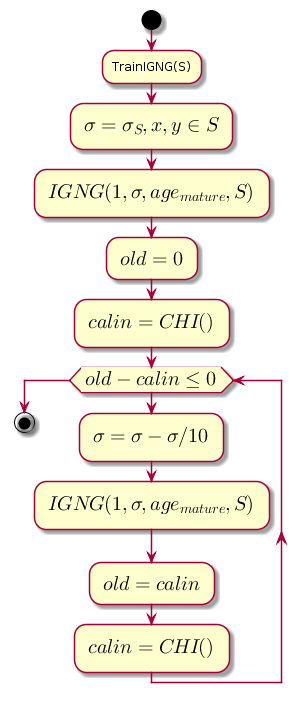
Основной цикл на каждом шаге уменьшает значение , которое является порогом близости, и высчитывает разницу между предыдущим уровнем качества кластеризации и уровнем, который был получен после кластеризации процедурой IGNG.
@startuml
start
:TrainIGNG(S);
:<latex>\sigma = \sigma_S,x,y \in S</latex>;
:<latex>IGNG(1, \sigma, age_{mature}, S)</latex>;
:<latex>old = 0</latex>;
:<latex>calin = CHI()</latex>;
while (<latex>old - calin \leq 0</latex>)
:<latex>\sigma=\sigma - \sigma / 10</latex>;
:<latex>IGNG(1, \sigma, age_{mature}, S)</latex>;
:<latex>old = calin</latex>;
:<latex>calin = CHI()</latex>;
endwhile
stop
@endumlCHI — это индекс Калинского-Харабаза, показывающий качество кластеризации:
Где:
— количество сэмплов данных.
— количество кластеров (в данном случае, количество нейронов).
— матрица внутренней дисперсии (сумма квадратов расстояний между координатами нейронов и средним по всем данным).
— матрица внешней дисперсии (сумма квадратов расстояний между всеми данными и ближайшим нейроном).
Чем больше значение индекса, тем лучше, потому если разность между индексами после кластеризации и до неё будет отрицательной, возможно считать, что индекс стал положительным и превысил предыдущий, т.е. кластеризация успешно выполнена.
Процедура IGNG
Это основная процедура алгоритма.
Она делится на три взаимоисключающих этапа:
- Нейронов не найдено.
- Найден один, удовлетворяющий условиям нейрон.
- Найдено два, удовлетворяющих условиям нейрона.
Если одно из условий проходит, другие этапы не выполняются.
Сначала ищется нейрон лучше всего приближайющий сэмпл данных:
Здесь — функция расчёта расстояния, которая обычно является Евклидовой метрикой.
Если нейрон не найден, либо он слишком далеко от данных, т.е. не удовлетворяет критерию приближённости , создаётся новый эмбриональный нейрон с координатами равными координатам сэмпла в пространстве данных.

Если же проверка на приближённость прошла, производится поиск второго нейрона аналогичным способом и проверка его на приближённость к сэмплу данных.
Если второй нейрон не найден, он создаётся.

Если были найдены два нейрона, удовлетворяющие условию близости к сэмплу данных, их координаты корректируются по следующей формуле:
Где:
— шаг адаптации.
— номер нейрона.
— функция соседства нейрона
с нейроном победителем (в данном случае, она вернёт 1 для прямых соседей, 0 в ином случае, потому шаг адаптации, для расчёта
будет ненулевым только для прямых соседей).
Иными словами, координата (вес) нейрона-победителя изменяются на , а всех его прямых соседей (тех, которые с ним связаны одним ребром графа) на
, где
— координата соответствующего нейрона до изменения.
Затем создаётся связь между двумя нейронами-победителями, а если она уже была создана, её возраст обнуляется.
Возраст всех других связей увеличивается.
Все связи, возраст которых превысил константу , удаляются.
После чего удаляются все изолированные (те, у которых нет связи с другими) зрелые нейроны.
Возраст непосредственных нейронов-соседей нейрона-победителя увеличивается.
Если возраст какого-либо из зародышевых нейронов превышает , он становится зрелым нейроном.
Окончательный граф содержит только зрелые нейроны.
Условием завершения процедуры IGNG ниже возможно считать фиксированное количество циклов.
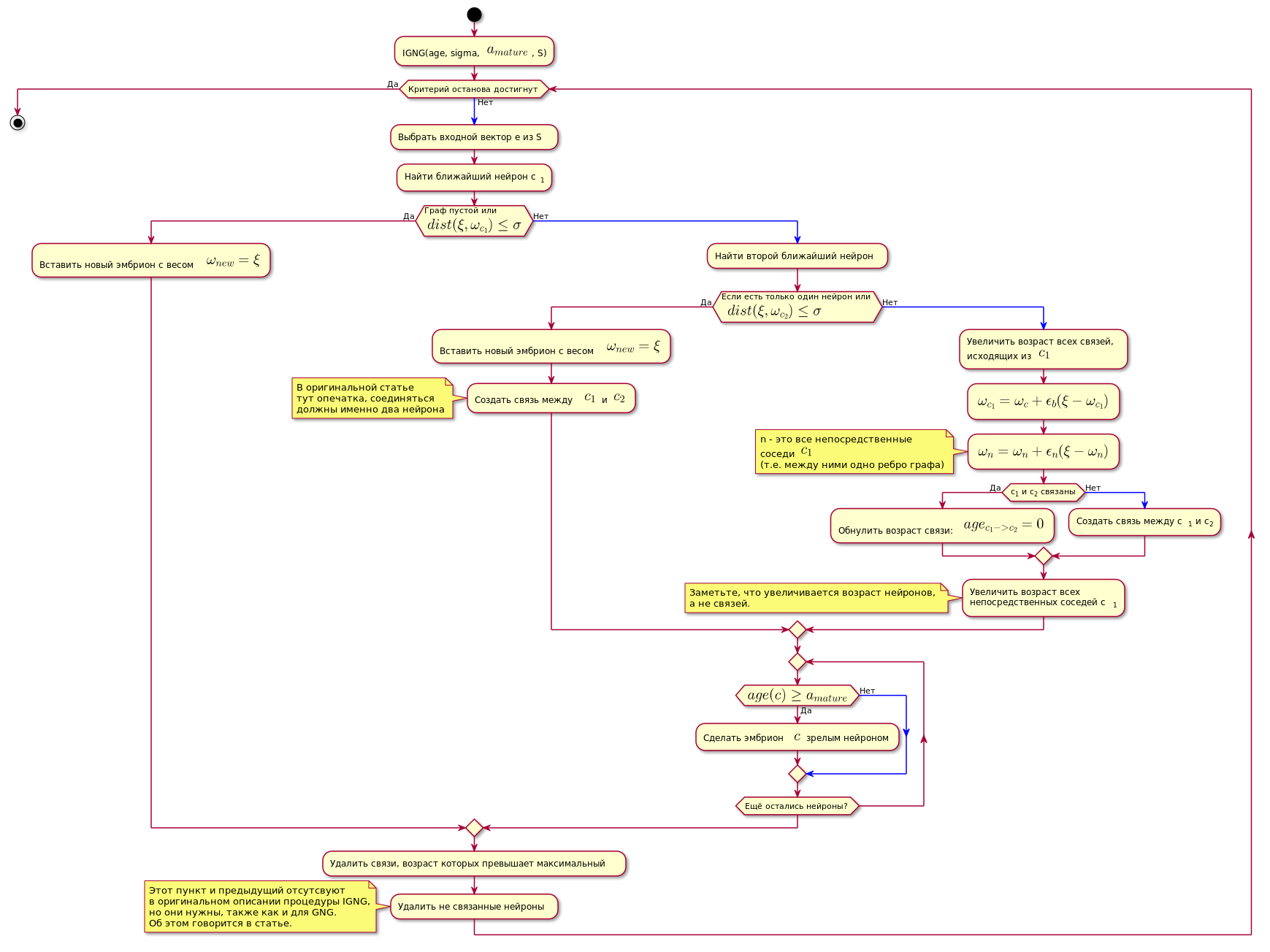
Ниже показан алгоритм (рисунок кликабелен):
@startuml
skinparam nodesep 10
skinparam ranksep 20
start
:IGNG(age, sigma, <latex>a_{mature}</latex>, S);
while (Критерий останова достигнут) is (Нет)
-[#blue]->
:Выбрать входной вектор e из S;
:Найти ближайший нейрон c<sub>1</sub>;
if (Граф пустой или\n<latex>dist(\xi, \omega_{c_1}) \leq \sigma</latex>) then (Да)
:Вставить новый эмбрион с весом <latex>\omega_{new} = \xi</latex>;
else (Нет)
-[#blue]->
:Найти второй ближайший нейрон;
if (Если есть только один нейрон или\n <latex>dist(\xi, \omega_{c_2}) \leq \sigma</latex>) then (Да)
:Вставить новый эмбрион с весом <latex>\omega_{new} = \xi</latex>;
:Создать связь между <latex>c_1</latex> и <latex>c_2</latex>;
note
В оригинальной статье
тут опечатка, соединяться
должны именно два нейрона
end note
else (Нет)
-[#blue]->
:Увеличить возраст всех связей,\nисходящих из <latex>c_1</latex>;
:<latex>\omega_{c_1} = \omega_c + \epsilon_b(\xi - \omega_{c_1})</latex>;
:<latex>\omega_n = \omega_n + \epsilon_n(\xi - \omega_n)</latex>;
note
n - это все непосредственные
соседи <latex>c_1</latex>
(т.е. между ними одно ребро графа)
end note
if (c<sub>1</sub> и c<sub>2</sub> связаны) then (Да)
:Обнулить возраст связи: <latex>age_{c_1 -> c_2} = 0</latex>;
else (Нет)
-[#blue]->
:Создать связь между c<sub>1</sub> и c<sub>2</sub>;
endif
:Увеличить возраст всех\nнепосредственных соседей c<sub>1</sub>;
note
Заметьте, что увеличивается возраст нейронов,
а не связей.
end note
endif
repeat
if (<latex>age(c) \geq a_{mature}</latex>) then (Да)
:Сделать эмбрион $<!-- math>c</math -->$ зрелым нейроном;
else (Нет)
-[#blue]->
endif
repeat while (Ещё остались нейроны?)
endif
:Удалить связи, возраст которых превышает максимальный;
:Удалить не связанные нейроны;
note
Этот пункт и предыдущий отсутсвуют
в оригинальном описании процедуры IGNG,
но они нужны, также как и для GNG.
Об этом говорится в статье.
endnote
endwhile (Да)
stop
@endumlРеализация
Реализация сети выполнена на Python, с использованием библиотеки графов NetworkX. Вырезка кода из прототипа в предыдущей статье приведена ниже. Там же есть краткие пояснения к коду.
Если кого-то интересует полный код, вот ссылка на репозиторий.
Пример работы алгоритма:

class NeuralGas():
__metaclass__ = ABCMeta
def __init__(self, data, surface_graph=None, output_images_dir='images'):
self._graph = nx.Graph()
self._data = data
self._surface_graph = surface_graph
# Deviation parameters.
self._dev_params = None
self._output_images_dir = output_images_dir
# Nodes count.
self._count = 0
if os.path.isdir(output_images_dir):
shutil.rmtree('{}'.format(output_images_dir))
print("Ouput images will be saved in: {0}".format(output_images_dir))
os.makedirs(output_images_dir)
self._start_time = time.time()
@abstractmethod
def train(self, max_iterations=100, save_step=0):
raise NotImplementedError()
def number_of_clusters(self):
return nx.number_connected_components(self._graph)
def detect_anomalies(self, data, threshold=5, train=False, save_step=100):
anomalies_counter, anomaly_records_counter, normal_records_counter = 0, 0, 0
anomaly_level = 0
start_time = self._start_time = time.time()
for i, d in enumerate(data):
risk_level = self.test_node(d, train)
if risk_level != 0:
anomaly_records_counter += 1
anomaly_level += risk_level
if anomaly_level > threshold:
anomalies_counter += 1
#print('Anomaly was detected [count = {}]!'.format(anomalies_counter))
anomaly_level = 0
else:
normal_records_counter += 1
if i % save_step == 0:
tm = time.time() - start_time
print('Abnormal records = {}, Normal records = {}, Detection time = {} s, Time per record = {} s'.
format(anomaly_records_counter, normal_records_counter, round(tm, 2), tm / i if i else 0))
tm = time.time() - start_time
print('{} [abnormal records = {}, normal records = {}, detection time = {} s, time per record = {} s]'.
format('Anomalies were detected (count = {})'.format(anomalies_counter) if anomalies_counter else 'Anomalies weren\'t detected',
anomaly_records_counter, normal_records_counter, round(tm, 2), tm / len(data)))
return anomalies_counter > 0
def test_node(self, node, train=False):
n, dist = self._determine_closest_vertice(node)
dev = self._calculate_deviation_params()
dev = dev.get(frozenset(nx.node_connected_component(self._graph, n)), dist + 1)
dist_sub_dev = dist - dev
if dist_sub_dev > 0:
return dist_sub_dev
if train:
self._dev_params = None
self._train_on_data_item(node)
return 0
@abstractmethod
def _train_on_data_item(self, data_item):
raise NotImplementedError()
@abstractmethod
def _save_img(self, fignum, training_step):
"""."""
raise NotImplementedError()
def _calculate_deviation_params(self, distance_function_params={}):
if self._dev_params is not None:
return self._dev_params
clusters = {}
dcvd = self._determine_closest_vertice
dlen = len(self._data)
#dmean = np.mean(self._data, axis=1)
#deviation = 0
for node in self._data:
n = dcvd(node, **distance_function_params)
cluster = clusters.setdefault(frozenset(nx.node_connected_component(self._graph, n[0])), [0, 0])
cluster[0] += n[1]
cluster[1] += 1
clusters = {k: sqrt(v[0]/v[1]) for k, v in clusters.items()}
self._dev_params = clusters
return clusters
def _determine_closest_vertice(self, curnode):
"""."""
pos = nx.get_node_attributes(self._graph, 'pos')
kv = zip(*pos.items())
distances = np.linalg.norm(kv[1] - curnode, ord=2, axis=1)
i0 = np.argsort(distances)[0]
return kv[0][i0], distances[i0]
def _determine_2closest_vertices(self, curnode):
"""Where this curnode is actually the x,y index of the data we want to analyze."""
pos = nx.get_node_attributes(self._graph, 'pos')
l_pos = len(pos)
if l_pos == 0:
return None, None
elif l_pos == 1:
return pos[0], None
kv = zip(*pos.items())
# Calculate Euclidean distance (2-norm of difference vectors) and get first two indexes of the sorted array.
# Or a Euclidean-closest nodes index.
distances = np.linalg.norm(kv[1] - curnode, ord=2, axis=1)
i0, i1 = np.argsort(distances)[0:2]
winner1 = tuple((kv[0][i0], distances[i0]))
winner2 = tuple((kv[0][i1], distances[i1]))
return winner1, winner2
class IGNG(NeuralGas):
"""Incremental Growing Neural Gas multidimensional implementation"""
def __init__(self, data, surface_graph=None, eps_b=0.05, eps_n=0.0005, max_age=5,
a_mature=1, output_images_dir='images'):
"""."""
NeuralGas.__init__(self, data, surface_graph, output_images_dir)
self._eps_b = eps_b
self._eps_n = eps_n
self._max_age = max_age
self._a_mature = a_mature
self._num_of_input_signals = 0
self._fignum = 0
self._max_train_iters = 0
# Initial value is a standard deviation of the data.
self._d = np.std(data)
def train(self, max_iterations=100, save_step=0):
"""IGNG training method"""
self._dev_params = None
self._max_train_iters = max_iterations
fignum = self._fignum
self._save_img(fignum, 0)
CHS = self.__calinski_harabaz_score
igng = self.__igng
data = self._data
if save_step < 1:
save_step = max_iterations
old = 0
calin = CHS()
i_count = 0
start_time = self._start_time = time.time()
while old - calin <= 0:
print('Iteration {0:d}...'.format(i_count))
i_count += 1
steps = 1
while steps <= max_iterations:
for i, x in enumerate(data):
igng(x)
if i % save_step == 0:
tm = time.time() - start_time
print('Training time = {} s, Time per record = {} s, Training step = {}, Clusters count = {}, Neurons = {}, CHI = {}'.
format(round(tm, 2),
tm / (i if i and i_count == 0 else len(data)),
i_count,
self.number_of_clusters(),
len(self._graph),
old - calin)
)
self._save_img(fignum, i_count)
fignum += 1
steps += 1
self._d -= 0.1 * self._d
old = calin
calin = CHS()
print('Training complete, clusters count = {}, training time = {} s'.format(self.number_of_clusters(), round(time.time() - start_time, 2)))
self._fignum = fignum
def _train_on_data_item(self, data_item):
steps = 0
igng = self.__igng
# while steps < self._max_train_iters:
while steps < 5:
igng(data_item)
steps += 1
def __long_train_on_data_item(self, data_item):
"""."""
np.append(self._data, data_item)
self._dev_params = None
CHS = self.__calinski_harabaz_score
igng = self.__igng
data = self._data
max_iterations = self._max_train_iters
old = 0
calin = CHS()
i_count = 0
# Strictly less.
while old - calin < 0:
print('Training with new normal node, step {0:d}...'.format(i_count))
i_count += 1
steps = 0
if i_count > 100:
print('BUG', old, calin)
break
while steps < max_iterations:
igng(data_item)
steps += 1
self._d -= 0.1 * self._d
old = calin
calin = CHS()
def _calculate_deviation_params(self, skip_embryo=True):
return super(IGNG, self)._calculate_deviation_params(distance_function_params={'skip_embryo': skip_embryo})
def __calinski_harabaz_score(self, skip_embryo=True):
graph = self._graph
nodes = graph.nodes
extra_disp, intra_disp = 0., 0.
# CHI = [B / (c - 1)]/[W / (n - c)]
# Total numb er of neurons.
#ns = nx.get_node_attributes(self._graph, 'n_type')
c = len([v for v in nodes.values() if v['n_type'] == 1]) if skip_embryo else len(nodes)
# Total number of data.
n = len(self._data)
# Mean of the all data.
mean = np.mean(self._data, axis=1)
pos = nx.get_node_attributes(self._graph, 'pos')
for node, k in pos.items():
if skip_embryo and nodes[node]['n_type'] == 0:
# Skip embryo neurons.
continue
mean_k = np.mean(k)
extra_disp += len(k) * np.sum((mean_k - mean) ** 2)
intra_disp += np.sum((k - mean_k) ** 2)
return (1. if intra_disp == 0. else
extra_disp * (n - c) /
(intra_disp * (c - 1.)))
def _determine_closest_vertice(self, curnode, skip_embryo=True):
"""Where this curnode is actually the x,y index of the data we want to analyze."""
pos = nx.get_node_attributes(self._graph, 'pos')
nodes = self._graph.nodes
distance = sys.maxint
for node, position in pos.items():
if skip_embryo and nodes[node]['n_type'] == 0:
# Skip embryo neurons.
continue
dist = euclidean(curnode, position)
if dist < distance:
distance = dist
return node, distance
def __get_specific_nodes(self, n_type):
return [n for n, p in nx.get_node_attributes(self._graph, 'n_type').items() if p == n_type]
def __igng(self, cur_node):
"""Main IGNG training subroutine"""
# find nearest unit and second nearest unit
winner1, winner2 = self._determine_2closest_vertices(cur_node)
graph = self._graph
nodes = graph.nodes
d = self._d
# Second list element is a distance.
if winner1 is None or winner1[1] >= d:
# 0 - is an embryo type.
graph.add_node(self._count, pos=copy(cur_node), n_type=0, age=0)
winner_node1 = self._count
self._count += 1
return
else:
winner_node1 = winner1[0]
# Second list element is a distance.
if winner2 is None or winner2[1] >= d:
# 0 - is an embryo type.
graph.add_node(self._count, pos=copy(cur_node), n_type=0, age=0)
winner_node2 = self._count
self._count += 1
graph.add_edge(winner_node1, winner_node2, age=0)
return
else:
winner_node2 = winner2[0]
# Increment the age of all edges, emanating from the winner.
for e in graph.edges(winner_node1, data=True):
e[2]['age'] += 1
w_node = nodes[winner_node1]
# Move the winner node towards current node.
w_node['pos'] += self._eps_b * (cur_node - w_node['pos'])
neighbors = nx.all_neighbors(graph, winner_node1)
a_mature = self._a_mature
for n in neighbors:
c_node = nodes[n]
# Move all direct neighbors of the winner.
c_node['pos'] += self._eps_n * (cur_node - c_node['pos'])
# Increment the age of all direct neighbors of the winner.
c_node['age'] += 1
if c_node['n_type'] == 0 and c_node['age'] >= a_mature:
# Now, it's a mature neuron.
c_node['n_type'] = 1
# Create connection with age == 0 between two winners.
graph.add_edge(winner_node1, winner_node2, age=0)
max_age = self._max_age
# If there are ages more than maximum allowed age, remove them.
age_of_edges = nx.get_edge_attributes(graph, 'age')
for edge, age in iteritems(age_of_edges):
if age >= max_age:
graph.remove_edge(edge[0], edge[1])
# If it causes isolated vertix, remove that vertex as well.
#graph.remove_nodes_from(nx.isolates(graph))
for node, v in nodes.items():
if v['n_type'] == 0:
# Skip embryo neurons.
continue
if not graph.neighbors(node):
graph.remove_node(node)
def _save_img(self, fignum, training_step):
"""."""
title='Incremental Growing Neural Gas for the network anomalies detection'
if self._surface_graph is not None:
text = OrderedDict([
('Image', fignum),
('Training step', training_step),
('Time', '{} s'.format(round(time.time() - self._start_time, 2))),
('Clusters count', self.number_of_clusters()),
('Neurons', len(self._graph)),
(' Mature', len(self.__get_specific_nodes(1))),
(' Embryo', len(self.__get_specific_nodes(0))),
('Connections', len(self._graph.edges)),
('Data records', len(self._data))
])
draw_graph3d(self._surface_graph, fignum, title=title)
graph = self._graph
if len(graph) > 0:
draw_graph3d(graph, fignum, clear=False, node_color=(1, 0, 0), title=title,
text=text)
mlab.savefig("{0}/{1}.png".format(self._output_images_dir, str(fignum)))
#mlab.close(fignum)