На протяжении многих лет я слежу за снукером, как за спортом. В нем есть всё: гипнотизирующая красота интеллектуальной игры, элегантность ударов киём и психологическая напряжённость соревнования. Но есть одна вещь, которая мне не нравится — его рейтинговая система.
Её основной недостаток заключается в том, что она учитывает только факт турнирного достижения без учёта "сложности" матчей. Такого недостатка лишена модель Эло, которая следит за "силой" игроков и обновляет её в зависимости от результатов матчей и "силы" соперника. Однако, и она подходит не идеально: считается, что все матчи проходят в равных условиях, а в снукере они играются до определённого количества выигранных фреймов (партий). Для учёта этого факта, я рассмотрел другую модель, которую назвал ЭлоБета.
В данной статье изучается качество моделей Эло и ЭлоБета на результатах снукерных матчей. Важно отметить, что основными целями являются оценка "силы" игроков и создание "справедливого" рейтинга, а не построение прогностических моделей для получения выгоды.
Текущий снукерный рейтинг основан на достижениях игрока в турнирах с их разной "весомостью". Давным давно учитывались только Чемпионаты Мира. После появления множества других соревнований была разработана таблица очков, которые игрок мог заработать, дойдя до определённой стадии турнира. Сейчас рейтинг имеет вид "скользящей" суммы призовых денег, которые игрок заработал в течение (приблизительно) крайних двух календарных лет.
У этой системы есть два главных преимущества: она простая (выигрывай много денег — поднимайся в рейтинге) и прогнозируемая (хочешь подняться на определённое место — выиграй определённое количество денег, при прочих равных). Проблема состоит в том, что при таком способе не учитывается сила (навык, форма) соперников. Обычным контр-аргументом является: "Если игрок достиг поздней стадии турнира, тогда он/она по определению является сильным игроком на текущий момент" ("слабые игроки не выигрывают турниры"). Звучит достаточно убедительно. Однако в снукере, как и в любом спорте, должна учитываться роль случая: если игрок "слабее", то это не означает, что он/она никогда не может выиграть в матче против игрока "сильнее". Просто это случается реже, чем обратный сценарий. Именно здесь выходит на сцену модель Эло.
Идея модели Эло заключается в том, что каждый игрок ассоциируется с числовым рейтингом. Вводится предположение о том, что результат игры между двумя игроками может быть предсказан, основываясь на разнице их рейтингов: большие значения означают большую вероятность победы "сильного" (с более высоким рейтингом) игрока. Рейтинг Эло основан на текущей "силе", вычисленной на основании результатов матчей с другими игроками. Это избегает основного недостатка текущей официальной рейтинговой системы. Такой подход также позволяет обновлять рейтинг игрока в течение турнира, чтобы численно реагировать на его хорошее выступление.
Имея практический опыт с рейтингом Эло, мне кажется, что он должен хорошо показать себя в снукере. Однако, есть одно препятствие: он создан для соревнований с единым типом матча. Конечно, существуют вариации для учёта преимуществ домашнего поля в футболе и первого хода в шахматах (обе в виде добавления фиксированного количества рейтинговых очков игроку с преимуществом). В снукере же матчи играются в формате "best of N": побеждает игрок, который первый выиграет фреймов (партий). Мы также будем называть этот формат "до
побед".
Интуитивно, победа в матче до 10 побед (финал серьёзного турнира) должна даваться сложнее "слабому" игроку, чем победа в матче до 4 побед (первый раунд текущих турниров Home Nations). Это учитывается в предложенной мной модели ЭлоБета.
Идея использования рейтинга Эло в снукере отнюдь не нова. Например, есть следующие работы:
- Snooker Analyst использует "Эло подобную" (больше похожую на модель Брэдли–Терри) рейтинговую систему. Идея заключается в обновлении рейтинга основываясь на разнице между "реальным" и "ожидаемым" количествами выигранных фреймов. Такой подход вызывает вопросы. Конечно, большая разница в количестве фреймов, скорее всего, демонстрирует большую разницу в силе, однако изначально у игрока не стоит такой задачи. В снукере цель "всего лишь" выиграть матч, т.е. выиграть определённое количество фреймов раньше соперника.
- Данное обсуждение на форуме с реализацией базовой модели Эло.
- Это и это реальные применения в любительском снукере.
- Возможно, существуют другие работы, которые я пропустил. Буду очень признателен за любую информацию по данной теме.
Обзор
Данная статья предназначена для пользователей языка R, заинтересованных в изучении рейтинга Эло, и для любителей снукера. Все эксперименты написаны с идеей быть воспроизводимыми. Код спрятан под спойлерами, имеет комментарии и использует пакеты tidyverse, так что может быть сам по себе интересен для чтения пользователям R. Предполагается последовательное выполнение всего представленного кода. Одним файлом его можно найти здесь.
Статья организована следующим образом:
- Раздел Модели описывает подходы Эло и ЭлоБета с реализацией в R.
- Раздел Эксперимент описывает детали и мотивацию вычисления: какие данные и методология используются (и почему), а также какие получены результаты.
- Раздел Изучение рейтингов ЭлоБета содержит результаты применения модели ЭлоБета к реальным снукерным данным. Он будет больше интересен любителям снукера.
Нам понадобится следующая инициализация.
# Пакеты для манипуляций с данными
suppressPackageStartupMessages(library(dplyr))
library(tidyr)
library(purrr)
# Пакет для визуализации
library(ggplot2)
# Пакет для рейтингов
suppressPackageStartupMessages(library(comperank))
theme_set(theme_bw())
# Не должно понадобиться. Просто на всякий случай.
set.seed(20180703)Модели
Обе модели основаны на следующих предположениях:
- Существует фиксированное множество игроков, которые должны быть проранжированы от "сильнейшего" (первое место) к "слабейшему" (последнее место).
- Ранжирование осуществляется ассоциированием игрока
с числовым рейтингом
: число, отображающее "силу" игрока (большее значение — сильнее игрок).
- Чем больше разница рейтингов перед матчем, тем менее вероятна победа "слабого" игрока (с меньшим рейтингом).
- Рейтинги обновляются после каждого матча на основании его результата и рейтингов до него.
- Победа над соперником "сильнее" должна сопровождаться большим приростом рейтинга, чем победа над соперником "слабее". При поражении верно обратное.
Эло
#' @details Данная функция векторизована по всем своим аргументам. Использование
#' `...` критично для возможности передачи других аргументов в будущем.
#'
#' @return Вероятность того, что игрок 1 (с рейтингом `rating1`) выиграет матч
#' против игрока 2 (рейтинг `rating2`). Разница рейтингов напрямую влияет на
#' результат.
elo_win_prob <- function(rating1, rating2, ksi = 400, ...) {
norm_rating_diff <- (rating2 - rating1) / ksi
1 / (1 + 10^norm_rating_diff)
}
#' @return Рейтинговая функция для модели Эло, которую можно передать в
#' `comperank::add_iterative_ratings()`.
elo_fun_gen <- function(K, ksi = 400) {
function(rating1, score1, rating2, score2) {
comperank::elo(rating1, score1, rating2, score2, K = K, ksi = ksi)[1, ]
}
}Модель Эло обновляет рейтинги по следующей процедуре:
Вычисление вероятности победы определённого игрока в матче (до его начала). Вероятность победы одного игрока (будем называть его/её "первым") с идентификатором
и рейтингом
над другим игроком ("вторым") с идентификатором
и рейтингом
равняется
При таком подходе вычисление вероятности подчиняется третьему предположению.
Нормировка разности на 400 — это математический способ сказать, какая разность считается "большой". Это число может быть заменено на параметр модели
, однако это влияет только на разброс будущих рейтингов и обычно является излишним. Значение 400 достаточно стандартно.
При общем подходе вероятность победы равняется
, где
некоторая строго возрастающая функция со значениями от 0 до 1. Мы будем использовать логистическую кривую. Более полное исследование можно найти в этой статье.
Вычисление результата матча
. В базовой модели он равняется 1 в случае победы первого игрока (поражения второго), 0.5 в случае ничьи и 0 в случае поражения первого игрока (победы второго).
Обновление рейтингов:
. Это величина, на которую изменятся рейтинги. Она использует коэффициент
(единственный параметр модели). Меньшее
(при равных вероятностях) означает меньшее изменение в рейтингах — модель более консервативна, т.е. необходимо больше побед для того, чтобы "доказать" изменение в силе. С другой стороны, большее
означает большее "доверие" недавним результатам, чем текущим рейтингам. Выбор "оптимального"
является способом создания "хорошей" рейтинговой системы.
,
.
Замечания:
- Как видно из формул обновления, сумма рейтингов всех учитываемых игроков не изменяется с течением времени: рейтинг увеличивается за счёт уменьшения рейтинга соперника
- Игроки без сыгранных матчей ассоциируются с начальным рейтингом 0. Обычно используются величины 1500 или 1000, однако я не вижу в этом никакой другой причины, кроме как психологической. С учётом предыдущего замечания использование нуля означает, что сумма всех рейтингов всегда равняется нулю, что по-своему красиво.
- Необходимо сыграть некоторое количество матчей для того, чтобы рейтинг отображал "силу" игрока. Это представляет проблему: новые добавленные игроки начинают с рейтингом 0, который наверняка не является наименьшим среди текущих игроков. Другими словами, "новички" считаются "сильнее", чем некоторые другие игроки. С этим можно стараться бороться внешними процедурами обновления рейтингов при вводе нового игрока.
Почему такой алгоритм имеет смысл? В случае равенства рейтингов
всегда равняется
. Допустим, например, что
и
. Это означает, что вероятность победы первого игрока равна
, т.е. он/она выиграет 1 матч из 11.
- В случае победы он/она получит прирост в приблизительно
, что больше, чем в случае равенства рейтингов.
- В случае поражения он/она получит уменьшение в приблизительно
, что меньше, чем в случае равенства рейтингов.
Это показывает, что модель Эло подчиняется пятому предположению: победа над соперником "сильнее" сопровождается большим приростом рейтинга, чем победа над соперником "слабее", и наоборот.
- В случае победы он/она получит прирост в приблизительно
Конечно, у модели Эло есть свои (достаточно высокоуровневые) практические особенности. Однако, наиболее важной для нашего исследования является следующая: предполагается, что все матчи проводятся в равных условиях. Это означает, что не учитывается дистанция матча: победа в матче до 4 побед вознаграждается так же, как победа в матче до 10 побед. Здесь выходит на сцену модель ЭлоБета.
ЭлоБета
#' @details Данная функция векторизована по всем своим аргументам.
#'
#' @return Вероятность того, что игрок 1 (с рейтингом `rating1`) выиграет матч
#' против игрока 2 (рейтинг `rating2`). Матч играется до `frames_to_win`
#' победных фреймов. Разница рейтингов напрямую влияет на вероятность победы
#' в одном фрейме.
elobeta_win_prob <- function(rating1, rating2, frames_to_win, ksi = 400, ...) {
prob_frame <- elo_win_prob(rating1 = rating1, rating2 = rating2, ksi = ksi)
# Вероятность того, что первый игрок выиграет `frames_to_win` фреймов раньше
# второго опираясь на вероятность первого игрока выиграть один фрейм
# (`prob_frame`). Фреймы считаются независимыми.
pbeta(prob_frame, frames_to_win, frames_to_win)
}
#' @return Результат матча в терминах победы первого игрока: 1 если он/она
#' выиграл(а), 0.5 в случае ничьи и 0 если он/она проиграл(а).
get_match_result <- function(score1, score2) {
# В снукере ничьи (обычно) не бывает, но это учитывает общий случай.
near_score <- dplyr::near(score1, score2)
dplyr::if_else(near_score, 0.5, as.numeric(score1 > score2))
}
#' @return Рейтинговая функция для модели ЭлоБета, которую можно передать в
#' `add_iterative_ratings()`.
elobeta_fun_gen <- function(K, ksi = 400) {
function(rating1, score1, rating2, score2) {
prob_win <- elobeta_win_prob(
rating1 = rating1, rating2 = rating2,
frames_to_win = pmax(score1, score2), ksi = ksi
)
match_result <- get_match_result(score1, score2)
delta <- K * (match_result - prob_win)
c(rating1 + delta, rating2 - delta)
}
}В модели Эло разница рейтингов напрямую влияет на вероятность победы во всём матче. Главной идеей модели ЭлоБета является прямое влияние разницы рейтингов на вероятность победы в одном фрейме и явное вычисление вероятности игрока выиграть фреймов раньше соперника.
Остаётся вопрос: как вычислить такую вероятность? Оказывается, это одна из старейших задач в истории теории вероятностей и имеет своё название — задача о разделении ставок (Problem of points). Очень приятное изложение можно найти в этой статье. Используя её обозначения, искомая вероятность равняется:
Здесь — вероятность первого игрока выиграть матч до
побед;
— вероятность его/её победы в одном фрейме (у соперника вероятность
). При таком подходе предполагается, что результаты фрейма внутри матча не зависят друг от друга. Это может подвергаться сомнению, но является необходимым предположением для данной модели.
Существует ли более быстрый способ вычисления? Оказывается, ответ положительный. После нескольких часов преобразования формул, практических экспериментов и поисков в интернете я нашёл следующее свойство у регуляризованной неполной бета-функции . Подставив
в это свойство и заменив
на
получается
.
Также это является хорошей новостью для пользователей R, т.к. может быть вычислено как
pbeta(p, n, n). Замечание: общий случай вероятности победы в фреймах раньше, чем соперник выиграет
, также может быть вычислено как
и
pbeta(p, n, m) соответственно. Это раскрывает богатые возможности по обновлению вероятности победы в течение матча.
Процедура обновления рейтингов в рамках модели ЭлоБета имеет следующий вид (при известных рейтингах и
, необходимом для победы количестве фреймов
и результате матча
, как в модели Эло):
- Вычисление вероятности победы первого игрока в одном фрейме:
.
- Вычисление вероятности победы этого игрока в матче:
. Например, если
равно 0.4, то вероятность победы в матче до 4 побед падает до 0.29, а в "до 18 побед" — до 0.11.
- Обновление рейтингов:
.
,
.
Замечание: т.к. разность рейтингов напрямую влияет на вероятность победы в одном фрейме, а не во всём матче, следует ожидать меньшее оптимальное значение коэффициента : часть значения
исходит от усиливающего эффекта
.
Идея вычисления результата матча на основании вероятности победы в одном фрейме не очень нова. На этом сайте авторства François Labelle можно найти онлайн вычисление вероятности победы в "best of " матче, наряду с другими функциями. Я был рад увидеть, что наши результаты вычислений совпадают. Однако, не смог найти никаких источников по введению такого подхода в процедуру обновления рейтингов Эло. Как и раньше, буду очень признателен за любую информацию по данной теме.
Я только смог найти эти статью и описание системы Эло на игровом сервере по нардам (FIBS). Есть также русскоязычный аналог. Здесь разная длительность матчей учитываются путём умножения разницы рейтингов на квадратный корень из дистанции матча. Однако, не похоже, чтобы это имело какого-то теоретического обоснования.
Эксперимент
У эксперимента есть несколько целей. На основании данных о результатах снукерных матчей:
- Определить лучшие значения коэффициента
для обеих моделей.
- Изучить устойчивость моделей в терминах точности прогнозной вероятности.
- Изучить эффект использования "пригласительных" турниров на рейтинги.
- Создать "справедливую" историю рейтингов за сезон 2017/18 для всех профессиональных игроков.
Данные
# Функция для разделения наблюдений по типам "train", "validation" и "test"
split_cases <- function(n, props = c(0.5, 0.25, 0.25)) {
breaks <- n * cumsum(head(props, -1)) / sum(props)
id_vec <- findInterval(seq_len(n), breaks, left.open = TRUE) + 1
c("train", "validation", "test")[id_vec]
}
pro_players <- snooker_players %>% filter(status == "pro")
# Матчи только между профессионалами
pro_matches_all <- snooker_matches %>%
# Используем только реально состоявшиеся матчи
filter(!walkover1, !walkover2) %>%
# Оставляем только матчи между профессионалами
semi_join(y = pro_players, by = c(player1Id = "id")) %>%
semi_join(y = pro_players, by = c(player2Id = "id")) %>%
# Добавляем столбец 'season'
left_join(
y = snooker_events %>% select(id, season), by = c(eventId = "id")
) %>%
# Обеспечиваем упорядоченность по времени окончания матча
arrange(endDate) %>%
# Подготавливаем к формату widecr
transmute(
game = seq_len(n()),
player1 = player1Id, score1, player2 = player2Id, score2,
matchId = id, endDate, eventId, season,
# Вычисляем тип матча ("train", "validation" или "test") в пропорции
# 50/25/25
matchType = split_cases(n())
) %>%
# Конвертируем в формат widecr
as_widecr()
# Матчи только между профессионалами в непригласительных турнирах (убираются, в
# основном, турниры Championship League).
pro_matches_off <- pro_matches_all %>%
anti_join(
y = snooker_events %>% filter(type == "Invitational"),
by = c(eventId = "id")
)
# Функция для подтверждение разбиения
get_split <- . %>% count(matchType) %>% mutate(share = n / sum(n))
# Это должно давать разбиение 50/25/25 (train/validation/test)
pro_matches_all %>% get_split()
## # A tibble: 3 x 3
## matchType n share
## <chr> <int> <dbl>
## 1 test 1030 0.250
## 2 train 2059 0.5
## 3 validation 1029 0.250
# Это даёт другое разбиение, потому что пригласительные турниры не распределены
# равномерно в течение сезона. Однако, при таком подходе матчи разбиты на
# основании тех же разделителей __по времени__, что и в `pro_matches_all`. Это
# гарантирует, что матчи с одним типом представляют одинаковые __периоды во
# времени__.
pro_matches_off %>% get_split()
## # A tibble: 3 x 3
## matchType n share
## <chr> <int> <dbl>
## 1 test 820 0.225
## 2 train 1810 0.497
## 3 validation 1014 0.278
# Сетка для коэффициента K
k_grid <- 1:100Мы будем использовать данные о снукере из пакета comperank. Оригинальным источником является сайт snooker.org. Результаты взяты из следующих матчей:
- Матч сыгран в сезоне 2016/17 или 2017/18.
- Матч является частью "профессионального" снукерного турнира, т.е.:
- Имеет тип "Invitational" ("Пригласительный"), "Qualifying" ("Квалификационный") или "Ranking" ("Рейтинговый"). Мы также будем отличать два набора матчей: "все матчи" (из всех данных турниров) и "официальные матчи" (без учёта пригласительных турниров). Для этого есть две причины:
- В пригласительных турнирах не все игроки имеют возможность изменить свой рейтинг. Это не обязательно плохо в рамках моделей Эло и ЭлоБета, но имеет "оттенок несправедливости".
- Есть убеждение, что игроки "относятся серьёзно" только к официальным рейтинговым матчам. Замечание: большинство "Invitational" турниров являются частью "Championship League", которая, как мне кажется, воспринимается большинством игроков
не очень серьёзнов виде практики с возможностью заработать денег. Присутствие этих турниров может повлиять на рейтинг. Помимо "Championship League" имеются другие пригласительные турниры: "2016 China Championship", оба "Champion of Champions", оба "Masters", "2017 Hong Kong Masters", "2017 World Games", "2017 Romanian Masters".
- Описывает традиционный снукер (не 6 красных или Power Snooker) между индивидуальными игроками (не командами).
- Оба пола могут принимать участие (не только мужчины или женщины).
- Игроки всех возрастов могут принимать участие (не только сеньоры или "under 21").
- Это не "Shoot-Out", т.к. эти турниры по другому хранятся в базе snooker.org.
- Имеет тип "Invitational" ("Пригласительный"), "Qualifying" ("Квалификационный") или "Ranking" ("Рейтинговый"). Мы также будем отличать два набора матчей: "все матчи" (из всех данных турниров) и "официальные матчи" (без учёта пригласительных турниров). Для этого есть две причины:
- Матч действительно состоялся: его результат является следствием реальной игры с участием обоих игроков.
- Матч проводится между двумя профессионалами. Список профессионалов взят за сезон 2017/18 (131 игрок). Это решение кажется наиболее противоречивым, т.к. удаление матчей с участием любителей "закрывает глаза" на поражения профессионалов от любителей. Это ведёт к несправедливому преимуществу данных игроков. Мне кажется, что такое решение необходимо для уменьшения инфляции рейтинга, которая произойдёт при учёте матчей с любителями. Другим подходом является изучение профессионалов и любителей вместе, но это кажется не обоснованным в рамках данного исследования. Поражение профессионала любителю считается потерей возможности повысить рейтинг.
Конечное количество используемых матчей равно 4118 для "всех матчей" и 3644 для "официальных матчей" (62.9 и 55.6 на одного игрока соответственно).
Методология
#' @param matches Объект класса `longcr` или `widecr` со столбцом `matchType`
#' (тип матча для эксперимента: "train", "validation" или "test").
#' @param test_type Тип матчей для вычисления качества модели. Для корректности
#' эксперимента все матчи этого типа должны были проводиться позже всех других
#' ("разогревочных") матчей. Это означает, что у них должны быть бОльшие
#' значения столбца `game`.
#' @param k_vec Вектор коэффициентов K для вычисления качества модели.
#' @param rate_fun_gen Функция, которая при передаче коэффициента K возвращает
#' рейтинговую функцию для передачи в `add_iterative_ratings()`.
#' @param get_win_prob Функция для вычисления вероятности победы на основании
#' рейтингов игроков (`rating1`, `rating2`) и количества фреймов, необходимого
#' для победы в матче (`frames_to_win`). __Замечание__: она должна быть
#' векторизована по всем своим аргументам.
#' @param initial_ratings Начальные рейтинги в формате для
#' `add_iterative_ratings()`.
#'
#' @details Данная функция вычисляет:
#' - Историю итеративных рейтингов после упорядочивания `matches` по возрастанию
#' столбца `game`.
#' - Для матчей с типом `test_type`:
#' - Вероятность победы игрока 1.
#' - Результат матча в терминах победы первого игрока: 1 если он/она
#' выиграл(а), 0.5 в случае ничьи и 0 если он/она проиграл(а).
#' - Качество в виде RMSE: квадратный корень из средней квадратичной ошибки, где
#' "ошибка" - разность между прогнозной вероятностью и результатом матча.
#'
#' @return Tibble со столбцами 'k' для коэффициента K и 'goodness' для
#' величины качества RMSE.
compute_goodness <- function(matches, test_type, k_vec, rate_fun_gen,
get_win_prob, initial_ratings = 0) {
cat("\n")
map_dfr(k_vec, function(cur_k) {
# Отслеживание хода выполнения
cat(cur_k, " ")
matches %>%
arrange(game) %>%
add_iterative_ratings(
rate_fun = rate_fun_gen(cur_k), initial_ratings = initial_ratings
) %>%
left_join(y = matches %>% select(game, matchType), by = "game") %>%
filter(matchType %in% test_type) %>%
mutate(
# Количество фреймов для победы в матче
framesToWin = pmax(score1, score2),
# Вероятность победы игрока 1 в матче до `framesToWin` побед
winProb = get_win_prob(
rating1 = rating1Before, rating2 = rating2Before,
frames_to_win = framesToWin
),
result = get_match_result(score1, score2),
squareError = (result - winProb)^2
) %>%
summarise(goodness = sqrt(mean(squareError)))
}) %>%
mutate(k = k_vec) %>%
select(k, goodness)
}
#' Обёртка для `compute_goodness()` для использования с матрицей эксперимента
compute_goodness_wrap <- function(matches_name, test_type, k_vec,
rate_fun_gen_name, win_prob_fun_name,
initial_ratings = 0) {
matches_tbl <- get(matches_name)
rate_fun_gen <- get(rate_fun_gen_name)
get_win_prob <- get(win_prob_fun_name)
compute_goodness(
matches_tbl, test_type, k_vec, rate_fun_gen, get_win_prob, initial_ratings
)
}
#' Функция для осуществления эксперимента
#'
#' @param test_type Вектор значений `test_type` (тип теста) для
#' `compute_goodness()`.
#' @param rating_type Имена рейтинговых моделей (типы рейтинга).
#' @param data_type Суффиксы типов данных.
#' @param k_vec,initial_ratings Величины для `compute_goodness()`.
#'
#' @details Данная функция генерирует матрицу эксперимента и вычисляет несколько
#' значений качества моделей для разных комбинаций типов рейтинга и данных. Для
#' того, чтобы она работала, в глобальном окружении необходимо наличие
#' переменных по следующими комбинациями имён:
#' - "pro_matches_" + `<типы теста>` + `<типы данных>` для результатов матчей.
#' - `<типы рейтинга>` + "_fun_gen" для генераторов рейтинговых функций.
#' - `<типы рейтинга>` + "_win_prob" для функций, вычисляющий вероятность
#' победы.
#'
#' @return Tibble со следующими столбцами:
#' - __testType__ <chr> : Идентификатор типа теста.
#' - __ratingType__ <chr> : Идентификатор типа рейтинга.
#' - __dataType__ <chr> : Идентификатор типа данных.
#' - __k__ <dbl/int> : Значение коэффициента K.
#' - __goodness__ <dbl> : Значение качества модели.
do_experiment <- function(test_type = c("validation", "test"),
rating_type = c("elo", "elobeta"),
data_type = c("all", "off"),
k_vec = k_grid,
initial_ratings = 0) {
crossing(
testType = test_type, ratingType = rating_type, dataType = data_type
) %>%
mutate(
dataName = paste0("pro_matches_", testType, "_", dataType),
kVec = rep(list(k_vec), n()),
rateFunGenName = paste0(ratingType, "_fun_gen"),
winProbFunName = paste0(ratingType, "_win_prob"),
initialRatings = rep(list(initial_ratings), n()),
experimentData = pmap(
list(dataName, testType, kVec,
rateFunGenName, winProbFunName, initialRatings),
compute_goodness_wrap
)
) %>%
unnest(experimentData) %>%
select(testType, ratingType, dataType, k, goodness)
}Для нахождения "оптимального" значения будем использовать равномерную решётку
. Учёт больших значений кажется не обоснованным, что подтверждается экспериментом. Используется следующая процедура:
- Для каждого
:
- Вычисление истории итеративных рейтингов определённой модели на основании определённого набора данных. Это означает, что на выходе будут известны рейтинги игроков перед каждым матчем. Это сделано с помощью функции
add_iterative_ratings()из пакетаcomperank. Такой подход описывает "онлайн рейтинги", т.е. обновление после каждого матча. - На основании данных, начиная с определённого (отстающего от начала) момента времени, вычисление качества модели. Будем использовать RMSE (квадратный корень из средней квадратичной ошибки) между результатом матча и вероятностью победы первого игрока (вычисленной на основании модели). Другими словами,
, где
— индексы используемых матчей,
— количество этих матчей,
— результат матча для первого игрока,
— вероятность победы первого игрока в матче (вычисленной на основании модели). Удаление матчей с начала данных необходимо для того, чтобы рейтинги успели отойти от начальных и начали отображать "текущую силу" игрока.
- Вычисление истории итеративных рейтингов определённой модели на основании определённого набора данных. Это означает, что на выходе будут известны рейтинги игроков перед каждым матчем. Это сделано с помощью функции
- Величина
с устойчивым минимальным RMSE объявляется оптимальной. Здесь под "устойчивым" понимается, что относительно малое значение RMSE присутствует в некоторой окрестности оптимального
(будет определено не очень строго путём рассматривания графиков). Значения меньше 0.5 (величина для "модели" с постоянным прогнозом 0.5) будет считаться успехом.
Так как одной из целей является изучение стабильности моделей, данные будут разбиты на три подмножества: "train" (обучающее), "validation" (валидационное) и "test" (тестовое). Они отсортированы по времени, т.е. любой матч из "train"/"validation" имеет время окончания раньше, чем любой матч из "validation"/"test". Я решил разбить данные в пропорции 50/25/25 для "всех матчей". Разбиение "официальных матчей" делается путём удаления из "всех матчей" пригласительных турниров. Это даёт не совсем желаемую пропорцию: 49.7/27.8/22.5. Однако, такой подход обеспечивает, что матчи одного типа представляют одинаковые периоды во времени.
Эксперимент будет проведён для всех комбинаций следующих переменных:
- Тип модели: Эло или ЭлоБета.
- Тип данных: "Все матчи" или "официальные матчи" (они же "офиц. матчи").
- Тип эксперимента: "Валидационный" (матчи "validation" используются для вычисления RMSE после "разогрева" на "train" матчах) и "Тестовый" (матчи "test" используются для вычисления RMSE после "разогрева" на "train" и "validation" матчах).
Результаты
pro_matches_validation_all <- pro_matches_all %>% filter(matchType != "test")
pro_matches_validation_off <- pro_matches_off %>% filter(matchType != "test")
pro_matches_test_all <- pro_matches_all
pro_matches_test_off <- pro_matches_off# Выполнение занимает существенное время
experiment_tbl <- do_experiment()plot_data <- experiment_tbl %>%
unite(group, ratingType, dataType) %>%
mutate(
testType = recode(
testType, validation = "Валидационный", test = "Тестовый"
),
groupName = recode(
group, elo_all = "Эло, все матчи", elo_off = "Эло, офиц. матчи",
elobeta_all = "ЭлоБета, все матчи",
elobeta_off = "ЭлоБета, офиц. матчи"
),
# Фиксация предпочтительного порядка
groupName = factor(groupName, levels = unique(groupName))
)
compute_optimal_k <- . %>% group_by(testType, groupName) %>%
slice(which.min(goodness)) %>%
ungroup()
compute_k_labels <- . %>% compute_optimal_k() %>%
mutate(label = paste0("K = ", k)) %>%
group_by(groupName) %>%
# Если оптимальное K в рамках одной панели находится справа от своей пары,
# её метке необходимо небольшое смещение вправо. Если слева - полное и
# небольшое смещение влево.
mutate(hjust = - (k == max(k)) * 1.1 + 1.05) %>%
ungroup()
plot_experiment_results <- function(results_tbl) {
ggplot(results_tbl) +
geom_hline(
yintercept = 0.5, colour = "#AA5555", size = 0.5, linetype = "dotted"
) +
geom_line(aes(k, goodness, colour = testType)) +
geom_vline(
data = compute_optimal_k,
mapping = aes(xintercept = k, colour = testType),
linetype = "dashed", show.legend = FALSE
) +
geom_text(
data = compute_k_labels,
mapping = aes(k, Inf, label = label, hjust = hjust),
vjust = 1.2
) +
facet_wrap(~ groupName) +
scale_colour_manual(
values = c(`Валидационный` = "#377EB8", `Тестовый` = "#FF7F00"),
guide = guide_legend(title = "Эксперимент", override.aes = list(size = 4))
) +
labs(
x = "Коэффициент K", y = "Качество модели (RMSE)",
title = "Лучшие значения качества моделей Эло и ЭлоБета почти равны",
subtitle = paste0(
'Использование официальных матчей (без пригласительных турниров) даёт ',
'более устойчивые результаты.\n',
'Оптимальные значения K из тестового эксперимента (с более длительным ',
'"разогревом") меньше, чем из валидационного.'
)
) +
theme(title = element_text(size = 13), strip.text = element_text(size = 12))
}
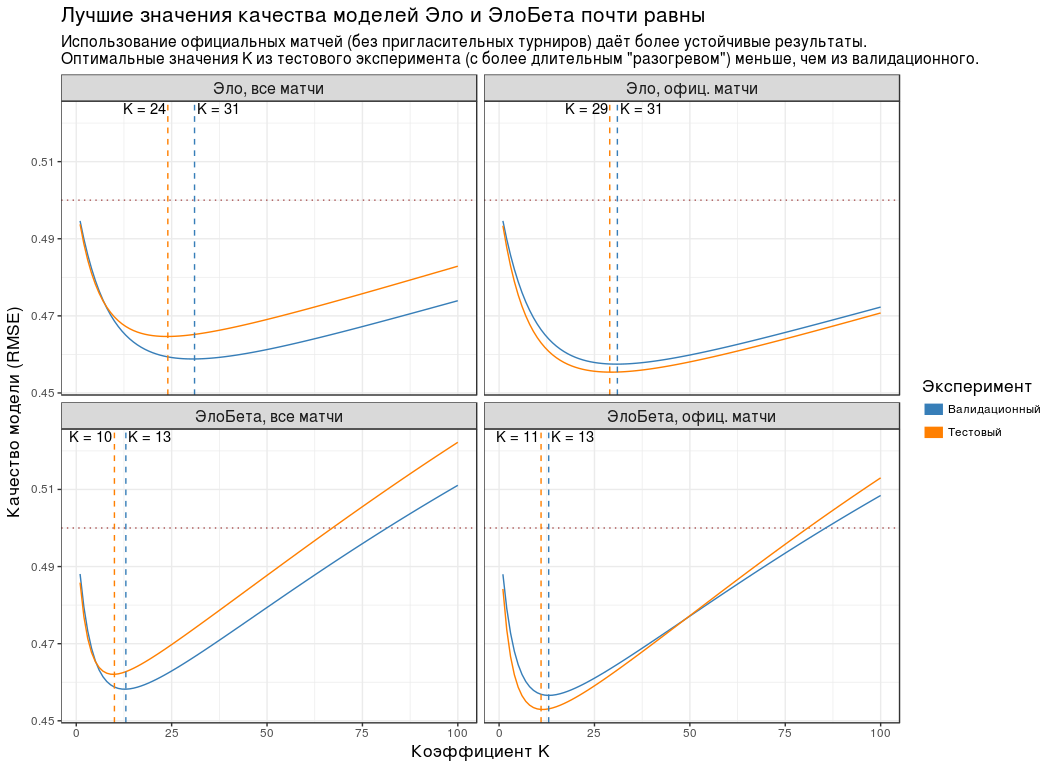
plot_experiment_results(plot_data)По результатам эксперимента можно сделать следующие выводы:
- Как и ожидалось, оптимальные значения
для ЭлоБета меньше, чем для Эло.
- Использование официальных матчей даёт более устойчивые результаты (результаты "Валидационного" и "Тестового" эксперимента отличаются меньше). Это не должно восприниматься как довод в сторону того, что профессионалы играют в пригласительных турнирах не серьёзно. Скорее это из-за качества результатов матчей из турнира "Championship League": он имеет слабо предсказуемый формат до 3 побед и очень плотный график.
- Изменение RMSE для оптимального
не сильно существенное. Другими словами, RMSE не изменяется значительно после вычисления оптимального
в "Валидационном" эксперименте и применении его в "Тестовом". Более того, для "официальных матчей" качество даже улучшилось.
- Все оптимальные значения
из тестового эксперимента (с более длительным "разогревом") меньше, чем из валидационного эксперимента. Это может как как следствием более длительного "разогрева", так и просто особенностью конкретных данных.
- Лучшие значения RMSE для обеих моделей на одних данных очень близки. Все устойчивы и меньше 0.5. Данные для тестового эксперимента представлены ниже.
| Группа | Оптимальное K | RMSE |
|---|---|---|
| Эло, все матчи | 24 | 0.465 |
| Эло, офиц. матчи | 29 | 0.455 |
| ЭлоБета, все матчи | 10 | 0.462 |
| ЭлоБета, офиц. матчи | 11 | 0.453 |
Т.к. качество не сильно отличается, можно округлить оптимальные из "официальных матчей" (они демонстрируют большую устойчивость) до 5: для модели Эло это 30, для ЭлоБета — 10.
На основании этих результатов я склонен заключить, что модели Эло с и ЭлоБета с
могут найти полезное применение в анализе официальных снукерных матчей. Однако, модель ЭлоБета учитывает различный формат матчей до
побед, поэтому из двух следует предпочесть её.
Изучение рейтингов ЭлоБета
Следующие результаты были вычислены используя "официальные матчи" с моделью ЭлоБета (). Все возможные выводы не следует рассматривать как личные по отношению какому-либо игроку.
Топ-16 на конец сезона 2017/18
# Вспомогательная функция
gather_to_longcr <- function(tbl) {
bind_rows(
tbl %>% select(-matches("2")) %>% rename_all(funs(gsub("1", "", .))),
tbl %>% select(-matches("1")) %>% rename_all(funs(gsub("2", "", .)))
) %>%
arrange(game)
}
# Извлечение лучшего значения коэффициента K
best_k <- experiment_tbl %>%
filter(testType == "test", ratingType == "elobeta", dataType == "off") %>%
slice(which.min(goodness)) %>%
pull(k)
#!!! Округляет к "красивому" числу, т.к. это не сильно влияет на качество !!!
best_k <- round(best_k / 5) * 5
# Вычисление рейтингов на момент окончания данных
elobeta_ratings <- rate_iterative(
pro_matches_test_off, elobeta_fun_gen(best_k), initial_ratings = 0
) %>%
rename(ratingEloBeta = rating_iterative) %>%
arrange(desc(ratingEloBeta)) %>%
left_join(
y = snooker_players %>% select(id, playerName = name), by = c(player = "id")
) %>%
mutate(rankEloBeta = order(ratingEloBeta, decreasing = TRUE)) %>%
select(player, playerName, ratingEloBeta, rankEloBeta)
elobeta_top16 <- elobeta_ratings %>%
filter(rankEloBeta <= 16) %>%
mutate(
rankChr = formatC(rankEloBeta, width = 2, format = "d", flag = "0"),
ratingEloBeta = round(ratingEloBeta, 1)
)
official_ratings <- tibble(
player = c(
5, 1, 237, 17, 12, 16, 224, 30,
68, 154, 97, 39, 85, 2, 202, 1260
),
rankOff = c(
2, 3, 4, 1, 5, 7, 6, 13,
16, 10, 8, 9, 26, 17, 12, 23
),
ratingOff = c(
905750, 878750, 751525, 1315275, 660250, 543225, 590525, 324587,
303862, 356125, 453875, 416250, 180862, 291025, 332450, 215125
)
)Топ-16 по модели ЭлоБета на конец сезона 2017/18 имеет следующий вид (официальные данные также взяты с сайта snooker.org):
| Игрок | ЭлоБета место | ЭлоБета рейтинг | Офиц. место | Офиц. рейтинг | Подъём места по ЭлоБета |
|---|---|---|---|---|---|
| Ronnie O'Sullivan | 1 | 128.8 | 2 | 905 750 | 1 |
| Mark J Williams | 2 | 123.4 | 3 | 878 750 | 1 |
| John Higgins | 3 | 112.5 | 4 | 751 525 | 1 |
| Mark Selby | 4 | 102.4 | 1 | 1 315 275 | -3 |
| Judd Trump | 5 | 92.2 | 5 | 660 250 | 0 |
| Barry Hawkins | 6 | 83.1 | 7 | 543 225 | 1 |
| Ding Junhui | 7 | 82.8 | 6 | 590 525 | -1 |
| Stuart Bingham | 8 | 74.3 | 13 | 324 587 | 5 |
| Ryan Day | 9 | 71.9 | 16 | 303 862 | 7 |
| Neil Robertson | 10 | 70.6 | 10 | 356 125 | 0 |
| Shaun Murphy | 11 | 70.1 | 8 | 453 875 | -3 |
| Kyren Wilson | 12 | 70.1 | 9 | 416 250 | -3 |
| Jack Lisowski | 13 | 68.8 | 26 | 180 862 | 13 |
| Stephen Maguire | 14 | 63.7 | 17 | 291 025 | 3 |
| Mark Allen | 15 | 63.7 | 12 | 332 450 | -3 |
| Yan Bingtao | 16 | 61.6 | 23 | 215 125 | 7 |
Некоторые наблюдения:
- Текущий официальный №1 Марк Селби помещён на 3 места ниже в ЭлоБета. Это может быть признаком того, что текущее распределение призовых денег не совсем отражает усилия, необходимые для их получения (в среднем).
- Наиболее "недооценёнными" официальной системой игроками являются Джек Лисовски (невероятная разница в 13 мест), Райан Дэй и Янь Бинтао (оба имеют разницу в 7 мест).
- Стюарт Бинэм помещён на 5 строчек выше по ЭлоБета. Наиболее вероятной причиной является то, что он не играл 6 месяцев из-за бана WPBSA. Его рейтинг ЭлоБета не изменялся в течение этого периода, но в официальном рейтинге он терял очки из-за его "скользящего" характера. Это наблюдение демонстрирует важное отличие между двумя подходами: официальная система хорошо учитывает отсутствие игры, а ЭлоБета — её результаты.
- Джадд Трамп и Нил Робертсон помещены на одинаковое место по обеим системам.
- По результатам ЭлоБета Алистер Картер (официальный №11), Энтони Макгилл (№14) и Люка Бресель (№15) не находятся в топ-16. Их "вытеснили" Джек Лисовски (№26), Янь Бинтао (№23) и Стивен Магуайр (№17).
Приведу пример прогнозов модели ЭлоБета. Вероятность того, что игрок №16 (Yan Bingtao) выиграет один фрейм у игрока №1 (Ronnie O'Sullivan) равна 0.404. В матче до 4 побед она падает до 0.299, в "до 10 побед" — 0.197 и в финале Чемпионата Мира до 18 побед — 0.125. По моему мнению, эти значения достаточно близки к реальности.
Коллективная эволюция рейтингов ЭлоБета
# Вспомогательные данные
seasons_break <- ISOdatetime(2017, 5, 2, 0, 0, 0, tz = "UTC")
# Вычисление эволюции рейтингов
elobeta_history <- pro_matches_test_off %>%
add_iterative_ratings(elobeta_fun_gen(best_k), initial_ratings = 0) %>%
gather_to_longcr() %>%
left_join(y = pro_matches_test_off %>% select(game, endDate), by = "game")
# Генерирование графика
plot_all_elobeta_history <- function(history_tbl) {
history_tbl %>%
mutate(isTop16 = player %in% elobeta_top16$player) %>%
ggplot(aes(endDate, ratingAfter, group = player)) +
geom_step(data = . %>% filter(!isTop16), colour = "#C2DF9A") +
geom_step(data = . %>% filter(isTop16), colour = "#22A01C") +
geom_hline(yintercept = 0, colour = "#AAAAAA") +
geom_vline(
xintercept = seasons_break, linetype = "dotted",
colour = "#E41A1C", size = 1
) +
geom_text(
x = seasons_break, y = Inf, label = "Конец 2016/17",
colour = "#E41A1C", hjust = 1.05, vjust = 1.2
) +
scale_x_datetime(date_labels = "%Y-%m") +
labs(
x = NULL, y = "Рейтинг ЭлоБета",
title = paste0(
"Большая часть текущего топ-16 определилась в конце сезона 2016/17"
),
subtitle = paste0(
"Победа в турнире хорошо заметна как существенный рост без падения в",
" конце."
)
) +
theme(title = element_text(size = 13))
}
plot_all_elobeta_history(elobeta_history)Эволюция топ-16 по ЭлоБета
# Вычисление данных графика
top16_rating_evolution <- elobeta_history %>%
# Функция `inner_join` позволяет оставить только игроков из `elobeta_top16`
inner_join(y = elobeta_top16 %>% select(-ratingEloBeta), by = "player") %>%
# Оставить матчи только из сезона 2017/18
semi_join(
y = pro_matches_test_off %>% filter(season == 2017), by = "game"
) %>%
mutate(playerLabel = paste(rankChr, playerName))
# Генерирование графика
plot_top16_elobeta_history <- function(elobeta_history) {
ggplot(elobeta_history) +
geom_step(aes(endDate, ratingAfter, group = player), colour = "#22A01C") +
geom_hline(yintercept = 0, colour = "#AAAAAA") +
geom_rug(
data = elobeta_top16,
mapping = aes(y = ratingEloBeta), sides = "r"
) +
facet_wrap(~ playerLabel, nrow = 4, ncol = 4) +
scale_x_datetime(date_labels = "%Y-%m") +
labs(
x = NULL, y = "Рейтинг ЭлоБета",
title = "Эволюция рейтинга ЭлоБета для топ-16 (на конец сезона 2017/18)",
subtitle = paste0(
"Ронни О'Салливан и Марк Уильямс провели успешный сезон 2017/18.\n",
"Как и Джек Лисовски: рост с отрицательного рейтинга до 13-го места."
)
) +
theme(title = element_text(size = 13), strip.text = element_text(size = 12))
}
plot_top16_elobeta_history(top16_rating_evolution)Выводы
- Решение "задачи о разделении ставок" в R крайне прямолинейно:
pbeta(p, n, m). - Модель ЭлоБета — это модификация модели Эло для матчей формата "best of
" (до
побед). Она учитывает различную дистанцию матча при обновлении рейтингов.
- Модели Эло с
и ЭлоБета с
могут найти полезное применение в анализе официальных снукерных матчей.
- Снукерные:
- Наиболее "недооценёнными" официальной системой игроками являются Джек Лисовски, Райан Дэй и Янь Бинтао.
- Сезон 2017/18 был очень успешным для Ронни О'Салливана, Марка Уильямса и Джека Лисовски.
sessionInfo()
## R version 3.4.4 (2018-03-15)
## Platform: x86_64-pc-linux-gnu (64-bit)
## Running under: Ubuntu 16.04.4 LTS
##
## Matrix products: default
## BLAS: /usr/lib/openblas-base/libblas.so.3
## LAPACK: /usr/lib/libopenblasp-r0.2.18.so
##
## locale:
## [1] LC_CTYPE=ru_UA.UTF-8 LC_NUMERIC=C
## [3] LC_TIME=ru_UA.UTF-8 LC_COLLATE=ru_UA.UTF-8
## [5] LC_MONETARY=ru_UA.UTF-8 LC_MESSAGES=ru_UA.UTF-8
## [7] LC_PAPER=ru_UA.UTF-8 LC_NAME=C
## [9] LC_ADDRESS=C LC_TELEPHONE=C
## [11] LC_MEASUREMENT=ru_UA.UTF-8 LC_IDENTIFICATION=C
##
## attached base packages:
## [1] stats graphics grDevices utils datasets methods base
##
## other attached packages:
## [1] bindrcpp_0.2.2 comperank_0.1.0 comperes_0.2.0 ggplot2_2.2.1
## [5] purrr_0.2.5 tidyr_0.8.1 dplyr_0.7.6
##
## loaded via a namespace (and not attached):
## [1] Rcpp_0.12.17 knitr_1.20 bindr_0.1.1 magrittr_1.5
## [5] munsell_0.5.0 tidyselect_0.2.4 colorspace_1.3-2 R6_2.2.2
## [9] rlang_0.2.1 highr_0.7 plyr_1.8.4 stringr_1.3.1
## [13] tools_3.4.4 grid_3.4.4 gtable_0.2.0 utf8_1.1.4
## [17] cli_1.0.0 htmltools_0.3.6 lazyeval_0.2.1 yaml_2.1.19
## [21] assertthat_0.2.0 rprojroot_1.3-2 digest_0.6.15 tibble_1.4.2
## [25] crayon_1.3.4 glue_1.2.0 evaluate_0.10.1 rmarkdown_1.10
## [29] labeling_0.3 stringi_1.2.3 compiler_3.4.4 pillar_1.2.3
## [33] scales_0.5.0 backports_1.1.2 pkgconfig_2.0.1
 Кликабельно
Кликабельно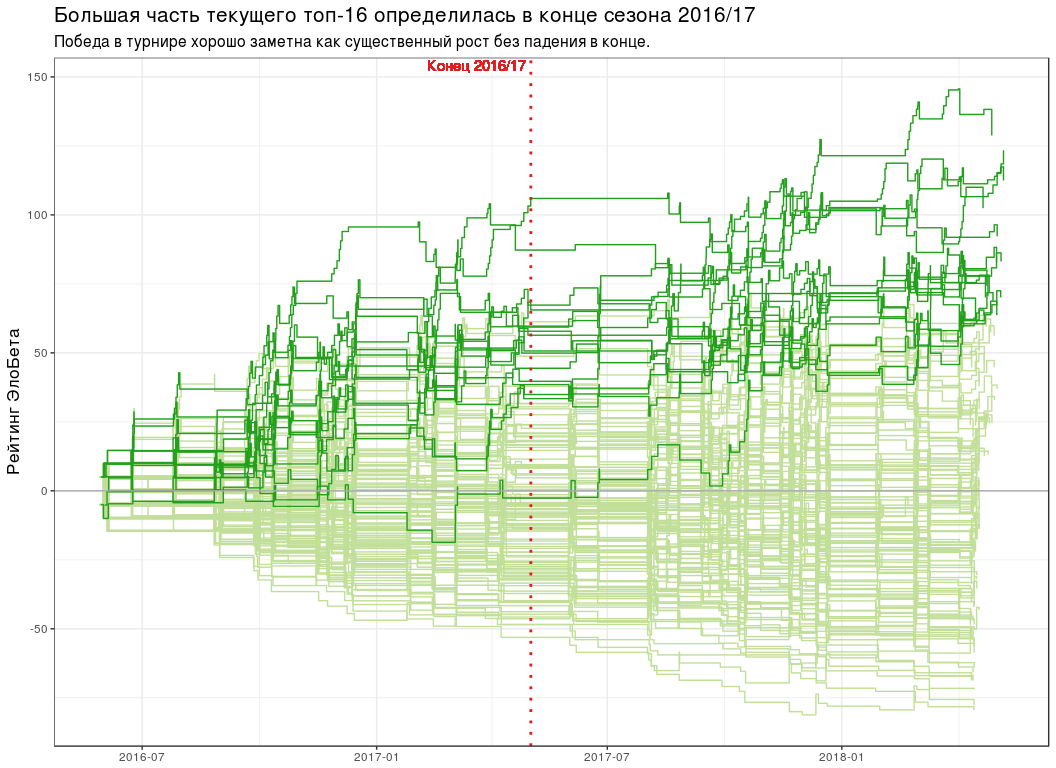 Опять кликабельно
Опять кликабельно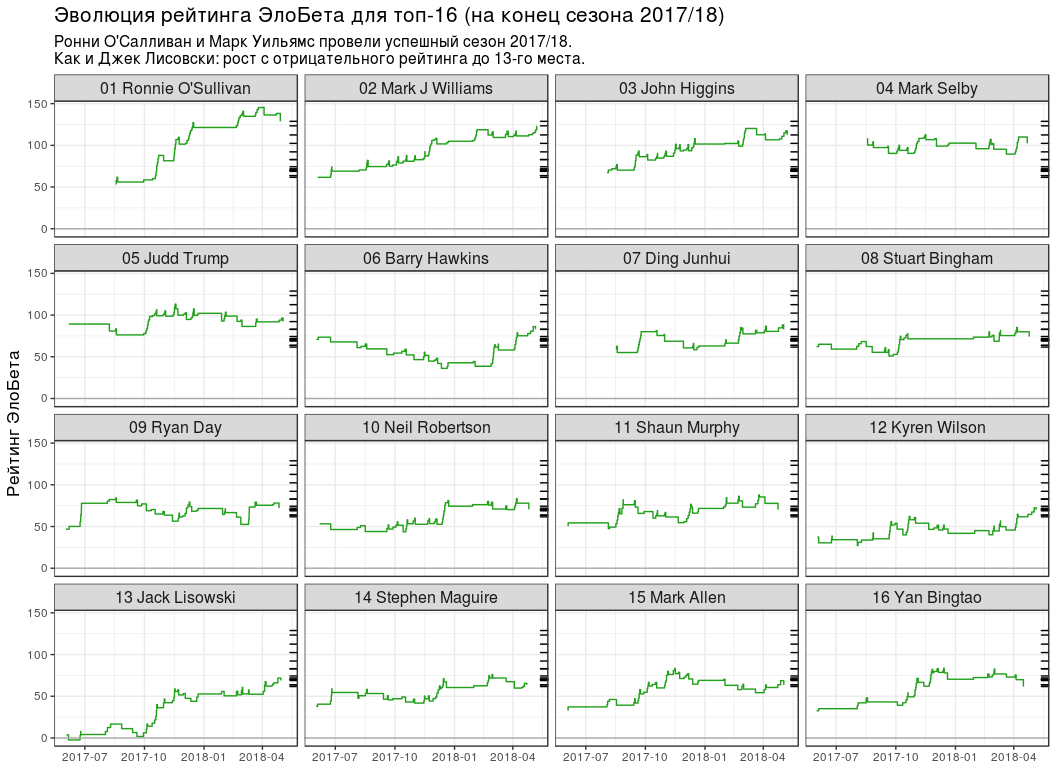 И снова кликабельно
И снова кликабельно