Во вчерашней серии футурамы поставили довольно интересную задачку — не мог не удержаться и не разобрать ее тут.

Итак, фабула такова: Профессор изобрел машину для обмена телами, которая, как оказалось, работает только в одну сторону. После нескольких перестановок герои оказались в тяжелой ситуации, в которой им предстояло придумать способ вернуться обратно в свои тела. Вот тут-то нам и поможет «чистая математика».
Итак, приступим. Пусть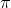 — это цикл длины k на множестве [n] = {1… n}. Без потери общности запишем:
— это цикл длины k на множестве [n] = {1… n}. Без потери общности запишем:

Пусть теперь (a, b) представляет собой транспозицию, которая меняет местами содержимое a и b.
По предположению,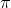 получена с помощью определенных подстановок над [n].
получена с помощью определенных подстановок над [n].
Введем два «новых тела» {x, y} и запишем

Для любых i = 1,… k запишем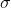 как ряд перестановок:
как ряд перестановок:
(x,2)...(x,i))((y,i+1)(y,i+2)(y,k))((x,i+1))((y,1)))
Заметим, что транспозиции меняют элемент из [n] с каким-либо элементом из {x, y}, поэтому все транспозиции отличаются от оных, образовавших исходную подстановку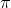 , а также от транспозиции (x, y). Простой проверкой получаем:
, а также от транспозиции (x, y). Простой проверкой получаем:

Таким образом,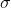 инвертирует цикл длины k, оставляя x и y переставленными без использования транспозиции (x, y).
инвертирует цикл длины k, оставляя x и y переставленными без использования транспозиции (x, y).
Теперь пусть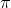 — случайная подстановка; она распадается на композицию независимых циклов, каждый из которых может быть инвертирован с использованием полученного выше алгоритма, после чего при необходимости можно поменять местами x и y, используя транспозицию (x, y).
— случайная подстановка; она распадается на композицию независимых циклов, каждый из которых может быть инвертирован с использованием полученного выше алгоритма, после чего при необходимости можно поменять местами x и y, используя транспозицию (x, y).
Так-то. А вы говорите, что у дискретки нет применений IRL.

Итак, фабула такова: Профессор изобрел машину для обмена телами, которая, как оказалось, работает только в одну сторону. После нескольких перестановок герои оказались в тяжелой ситуации, в которой им предстояло придумать способ вернуться обратно в свои тела. Вот тут-то нам и поможет «чистая математика».
Итак, приступим. Пусть
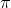 — это цикл длины k на множестве [n] = {1… n}. Без потери общности запишем:
— это цикл длины k на множестве [n] = {1… n}. Без потери общности запишем:
Пусть теперь (a, b) представляет собой транспозицию, которая меняет местами содержимое a и b.
По предположению,
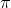 получена с помощью определенных подстановок над [n].
получена с помощью определенных подстановок над [n].Введем два «новых тела» {x, y} и запишем

Для любых i = 1,… k запишем
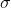 как ряд перестановок:
как ряд перестановок:(x,2)...(x,i))((y,i+1)(y,i+2)(y,k))((x,i+1))((y,1)))
Заметим, что транспозиции меняют элемент из [n] с каким-либо элементом из {x, y}, поэтому все транспозиции отличаются от оных, образовавших исходную подстановку
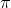 , а также от транспозиции (x, y). Простой проверкой получаем:
, а также от транспозиции (x, y). Простой проверкой получаем:
Таким образом,
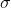 инвертирует цикл длины k, оставляя x и y переставленными без использования транспозиции (x, y).
инвертирует цикл длины k, оставляя x и y переставленными без использования транспозиции (x, y).Теперь пусть
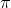 — случайная подстановка; она распадается на композицию независимых циклов, каждый из которых может быть инвертирован с использованием полученного выше алгоритма, после чего при необходимости можно поменять местами x и y, используя транспозицию (x, y).
— случайная подстановка; она распадается на композицию независимых циклов, каждый из которых может быть инвертирован с использованием полученного выше алгоритма, после чего при необходимости можно поменять местами x и y, используя транспозицию (x, y).Так-то. А вы говорите, что у дискретки нет применений IRL.
