
Небольшое введение
Начнем с тех случаев, когда вообще решается задача сопоставления изображений. Я могу перечислить следующие: создание панорам, создание стереопары и реконструкция трехмерной модели объекта по его двумерным проекциям в принципе, распознавание объектов и поиск по образцу из какой-то базы, слежение за движением объекта по нескольким снимкам, реконструкция аффинных преобразований изображений. Возможно какое-то применение в этом списке я упустил или этого применения ещё не придумали, но, наверно, и так уже можно составить представление о том какой круг задач призвано решать применение дескрипторов. Следует отметить, что область знаний, рассматривающая такого рода задачи (компьютерное зрение) достаточно молода, со всеми вытекающими отсюда последствиями. Нет определенного универсального метода, решающего все вышеперечисленные проблемы в полном объеме, т.е. для всех входных изображении. Однако, не все так плохо, просто надо знать, что существуют методы решения разного рода более узких задач, и понимать, что многое в выборе метода решения задачи зависит непосредственно от типа самой задачи, типа объектов и характера сцены, на которой они изображены и ваших личных предпочтений.
Так же, перед прочтением будет не лишним по диагонали посмотреть статью о методе SURF.
Общие размышления
Человек может сравнить изображения и выделять на них объекты визуально, на интуитивном уровне. Однако, для машины изображение — всего лишь ни о чем не говорящий набор данных. В общих чертах можно описать два подхода к тому, чтобы как-то «наделить» машину этим человеческим умением.
Есть определенные методы для сравнения изображений, основанные на сопоставлении знаний об изображениях в целом. В общем случае это выглядит следующим образом: для каждой точки изобра��ения вычисляется значение определённой функции, на основании этих значений можно приписать изображению определённую характеристику, тогда задача сравнения изображений сводится к задаче сравнения таких характеристик. По большому счету, эти методы настолько же плохи, насколько просты, и работают приемлемо, практически, только в идеальных ситуациях. Причин этому предостаточно: появление новых объектов на изображении, перекрытие одних объектов другими, шумы, изменения масштаба, положения объекта на изображении, положения камеры в трехмерном пространстве, освещения, аффинные преобразования и т.д. Собственно, плохие качества этих методов обусловлены их основной идеей, т.е. тем, что в характеристику вносит вклад каждая точка изображения, каким бы плохим этот вклад не был.
Последняя фраза сразу наталкивает на мысли обхода таких проблем: надо или как-то выбирать точки, вносящие вклад в характеристику, или, ещё лучше, выделять некоторые особые (ключевые) точки и сравнивать их. На этом мы и подошли к идее сопоставления изображений по ключевым точкам. Можно сказать, что мы заменяем изображение некоторой моделью — набором его ключевых точек. Сразу отметим, что особой будет называться такая точка изображенного объекта, которая с большой долей вероятности будет найдена на другом изображении этого же объекта. Детектором будем называть метод извлечения ключевых точек из изображения. Детектор должен обеспечивать инвариантность нахождения одних и тех же особых точек относительно преобразований изображений.
Единственно, что остается непонятным — каким образом определять какая ключевая точка одного изображения соответствует ключевой точке другого изображения. Ведь после применения детектора можно определить только координаты особых точек, а они на каждом изображении разные. Тут в дело и вступают дескрипторы. Дескриптор — идентификатор ключевой точки, выделяющий её из остальной массы особых точек. В свою очередь, дескрипторы должны обеспечивать инвариантность нахождения соответствия между особыми точками относительно преобразований изображений.
В итоге получается следующая схема решения задачи сопоставления изображений:
1. На изображениях выделяются ключевые точки и их дескрипторы.
2. По совпадению дескрипторов выделяются соответствующие друг другу ключевые точки.
3. На основе набора совпавших ключевых точек строится модель преобразования изображений, с помощью которого из одного изображения можно получить другое.
На каждом этапе есть свои проблемы и различные методы их решения, что вносит определенный произвол в решение первоначальной задачи. Далее будем рассматривать первую часть решения, а именно выделение особых точек и их дескрипторов методом SIFT ( Scale Invariant Feature Transform). В основном будет описан алгоритм метода SIFT, а не то, почему этот алгоритм работает, и выглядит именно так.
На последок перечислим некоторые преобразования, относительно которых мы бы хотели получить инвариантность:
1) смещения
2) поворот
3) масштаб (один и тот же объект может быть разных размеров на различных изображениях)
4) изменения яркости
5) изменения положения камеры
Инвариантность относительно трех последних преобразований в полной мере получить не удастся, но хотя бы частично сделать это уже было бы не плохо.
Нахождение особых точек
Основным моментом в детектировании особых точек является построение пирамиды гауссианов (Gaussian) и разностей гауссианов (Difference of Gaussian, DoG). Гауссианом (или изображением, размытым гауссовым фильтром) является изображение
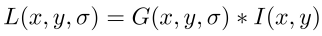
Здесь L — значение гауссиана в точке с координатами (x,y), а sigma — радиус размытия. G — гауссово ядро, I — значение исходного изображения, * — операция свертки.
Разностью гауссианов называют изображение, полученное путем попиксельного вычитания одного гауссина исходного изображения из гауссиана с другим радиусом рзмытия.
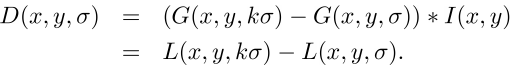
В двух словах скажем о масштабируемых пространствах. Масштабируемым пространством изображения является набор всевозможных, сглаженных некоторым фильтром, версий исходного изображения. Доказано, что гауссово масштабируемое пространство является линейным, инвариантным относительно сдвигов, вращений, масштаба, не смещающим локальные экстремумы, и обладает свойством полугрупп. Для нас важно, что различная степень размытия изображения гауссовым фильтром может быть принята за исходное изображение, взятое в некотором масштабе.
В общем, инвариантность относительно масштаба достигается за счет нахождения ключевых точек для исходного изображения, взятого в разных масштабах. Для этого строится пирамида гауссианов: все масштабируемое пространство разбивается на некоторые участки — октавы, причем часть масштабируемого пространства, занимаемого следующей октавой, в два раза больше части, занимаемой предыдущей. К тому же, при переходе от одной октавы к другой делается ресэмплинг изображения, его размеры уменьшаются вдвое. Естественно, что каждая октава охватывает бесконечное множество гауссианов изображения, поэтому строится только некоторое их количество N, с определенным шагом по радиусу размытия. С тем же шагом достраиваются два дополнительных гауссиана (всего получается N+2), выходящие за пределы октавы. Далее будет видно, зачем это нужно. Масштаб первого изображения следующей октавы равен масштабу изображения из предыдущей октавы с номером N.
Параллельно с построением пирамиды гауссианов, строится пирамида разностей гауссианов, состоящая из разностей соседних изображений в пирамиде гауссианов. Соответственно, количество изображений в этой пирамиде будет N+1.
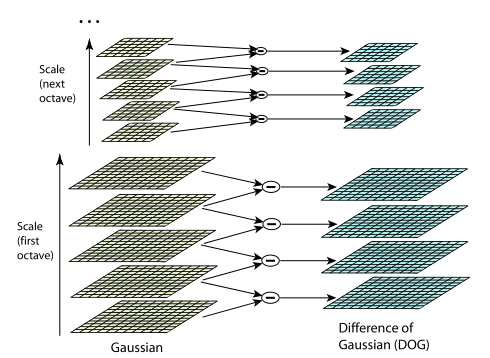
На рисунке слева изображена пирамида гауссианов, а справа — их разностей. Схематично показано, что каждая разность получается из двух соседних гауссианов, количество разностей на единицу меньше количества гауссианов, при переходе к следующей октаве размер изображений уменьшается вдвое
После построения пирамид дело остаётся за малым. Будем считать точку особой, если она является локальным экстремумом разности гауссианов. Для поиска экстремумов будем использовать метод, схематично изображенный на рисунке
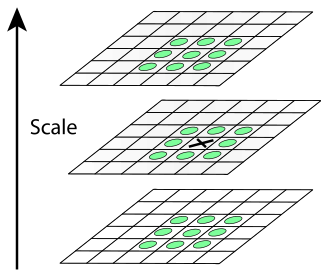
Если значение разности гауссианов в точке, помеченной крестиком, больше (меньше) всех значений в точках, помеченных кругляшками, то эта точка считается точкой экстремума
В каждом изображении из пирамиды DoG ищутся точки локального экстремума. Каждая точка текущего изображения DoG сравнивается с её восьмью соседями и с девятью соседями в DoG, находящихся на уровень выше и ниже в пирамиде. Если эта точка больше (меньше) всех соседей, то она принимается за точку локального экстремума.
Думаю теперь должно быть понятно, зачем нам понадобились «лишние» изображения в октаве. Для того, чтобы проверить на наличие точек экстремума N'e изображение в DoG пирамиде, нужно иметь N+1'е. А для того, чтобы получить N+1'е в DoG пирамиде, надо иметь N+1'е и N+2'е изображения в пирамиде гауссианов. Следуя той же логике можно сказать, что нужно строить 0'е изображение (для проверки 1'го) в пирамиде DoG и ещё два в пирамиде гауссианов. Но вспомнив, что 1'е изображение в текущей октаве имеет тот же масштаб, что и N'е в предыдущей (которое уже должно быть проверено) можем немного расслабиться и читать дальше :)
Уточнение особых точек
Как это ни странно, на предыдущем пункте поиск ключевых точек не окончен. Следующим шагом будет пара проверок пригодности точки экстремума на роль ключевой.
Первым делом определяются координаты особой точки с субпиксельной точностью. Это достигается с помощью аппроксимирования функции DoG многочленом Тейлора второго порядка, взятого в точке вычисленного экстремума.
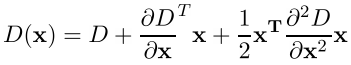
Здесь D — функция DoG, X = (x,y,sigma) — вектор смещения относительно точки разложения, первая производная DoG — градиент, вторая производная DoG — матрица Гессе.
Экстремум многочлена Тейлора находится путем вычисления производной и приравнивания ее к нулю. В итоге получим смещение точки вычисленного экстремума, относительно точного
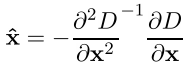
Все производные вычисляются по формулам конечных разностей. В итоге получаем СЛАУ размерности 3x3, относительно компонент вектора X^.
Если одна из компонент вектора X^ больше 0.5*шаг_сетки_в_этом_направлении, то это означает, что на самом деле точка экстремума была вычислена неверно и нужно сдвинуться к соседней точке в направлении указанных компонент. Для соседней точки все повторяется заново. Если таким образом мы вышли за пределы октавы, то следует исключить данную точку из рассмотрения.
Когда положение точки экстремума вычислено, проверяется на малость само значение DoG в этой точке по формуле
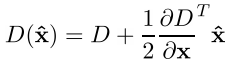
Если эта проверка не проходит, то точка исключается, как точка с малым контрастом.
Наконец, последняя проверка. Если особая точка лежит на границе какого-то объекта или плохо освещена, то такую точку можно исключить из рассмотрения. Эти точки имеют большой изгиб (одна из компонент второй производной) вдоль границы и малый в перпендикулярном направлении. Этот большой изгиб определяется матрицей Гессе H. Для проверки подойдет H размера 2x2.
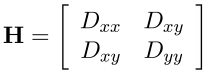
Пусть Tr(H) — след матрицы, а Det(H) — её определитель.
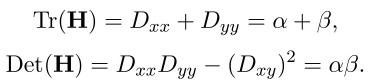
Пусть r — отношение большего изгиба к меньшему,
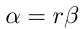
тогда
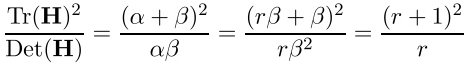
и точка рассматривается дальше, если
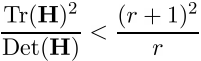
Нахождение ориентации ключевой точки
После того, как мы убедились, что какая-то точка является ключевой, нужно вычислить её ориентацию. Как будет видно далее, точка может иметь несколько направлений.
Направление ключевой точки вычисляется исходя из направлений градиентов точек, соседних с особой. Все вычисления градиентов производятся на изображении в пирамиде гауссианов, с масштабом наиболее близким к масштабу ключевой точки. Для справки: величина и направление градиента в точке (x,y) вычисляются по формулам
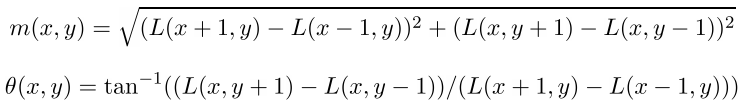
m — величина градиента, theta — его направление
Для начала определим окно (окрестность) ключевой точки, в котором будут рассмотрены градие��ты. По сути, это будет окно, требуемое для свертки с гауссовым ядром, причем оно будет круглым и радиус размытия для этого ядра (sigma) равен 1.5*масштаб_ключевой_точки. Для гауссова ядра действует так называемое правило «трех сигм». Оно состоит в том, что значение гауссова ядра очень близко к нулю на расстоянии, превышающем 3*sigma. Таким образом, радиус окна определяется как [3*sigma].
Направление ключевой точки найдем из гистограммы направлений O. Гистограмма состоит из 36 компонент, которые равномерно покрывают промежуток в 360 градусов, и формируется она следующим образом: каждая точка окна (x, y) вносит вклад, равный m*G(x, y, sigma), в ту компоненту гистограммы, которая покрывает промежуток, содержащий направление градиента theta(x, y).
Направление ключевой точки лежит в промежутке, покрываемом максимальной компонентой гистограммы. Значения максимальной компоненты (max) и двух соседних с ней интерполируются параболой, и точка максимума этой параболы берётся в качестве направления ключевой точки. Если в гистограмме есть ещё компоненты с величинами не меньше 0.8*max, то они аналогично интерполируются и дополнительные направления приписываются ключевой точке.
Построение дескрипторов
Теперь перейдем непосредственно к дескрипторам. Данное ранее определение говорит о том, что должен делать дескриптор, но не о том, что это такое. В принципе, дескриптором может выступать любой объект (лишь бы он справлялся со своими функциями), но обычно дескриптором является некая информация об окрестности ключевой точки. Такой выбор сделан в силу нескольких причин: на маленькие области меньшее влияние оказывают эффекты искажений, некоторые изменения (изменение положения объекта на картинке, изменение сцены, перекрытие одного объекта другим, поворот) могут не повлиять на дескриптор вовсе.
В методе SIFT дескриптором является вектор. Как и направление ключевой точки, дескриптор вычисляется на гауссиане, ближайшем по масштабу к ключевой точке, и исходя из градиентов в некотором окне ключевой точки. Перед вычислением дескриптора это окно поворачивают на угол направления ключевой точки, чем и достигается инвариантность относительно поворота. Для начала посмотрим на рисунок
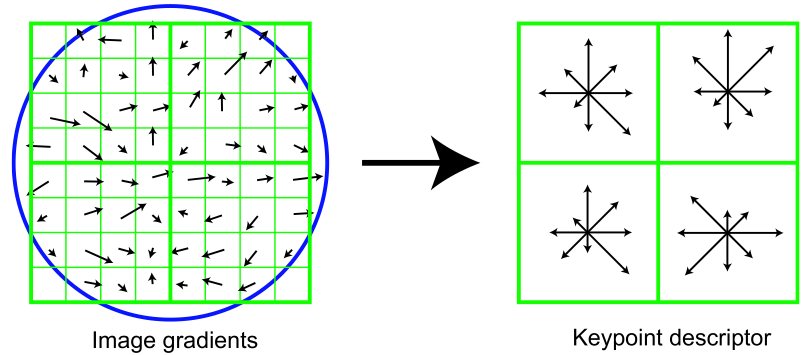
Здесь схематично показана часть изображения (слева) и (справа) полученный на её основе дескриптор. Для начала посмотрим налево. Здесь вы можете видеть пиксели, обозначенные маленькими квадратиками. Эти пиксели берутся из квадратного окна дескриптора, которое в свою очередь поделено ещё на четыре равных части (дальше будем называть их регионами). Маленькая стрелочка, в центре каждого пикселя обозначает градиент этого пикселя. Интересно то, что центр этого окна находится между пикселями. Его надо выбирать как можно ближе к точным координатам ключевой точки. Последняя деталь, которую можно увидеть — это круг, обозначающий окно свертки с гауссовым ядром (аналогично окну для вычисления направления ключевой точки). Для этого ядра определяется sigma, равное половине ширины окна дескриптора. В дальнейшем значение каждой точки окна дескриптора будет домножаться на значение гауссова ядра в этой точке, как на весовой коэффициент.
Теперь посмотрим направо. Здесь мы можем видеть схематически изображенный дескриптор особой точки, размерности 2x2x8. Первые две цифры в значении размерности — это количество регионов по горизонтали и вертикали. Те квадраты, которые охватывали некоторый регион пикселей на левом изображений, справа охватывают гистограммы, построенные на пикселях этих регионов. Соответственно, третья цифра в размерности дескриптора означает количество компонент гистограммы этих регионов. Гистограммы в регионах вычисляются так же, как и гистограмма направлений с тремя небольшими но:
1. Каждая гистограмма так же покрывает участок в 360 градусов, но делит его на 8 частей
2. В качестве весового коэффициента берется значение гауссова ядра, общего для всего дескриптора (об этом уже говорилось)
3. В качестве ещё одних весовых коэффициентов берутся коэффициенты трилинейной интерполяции.
Каждому градиенту в окне дескриптора можно приписать три вещественные координаты (x, y, n), где x — расстояние до градиента по горизонтали, y — расстояние по вертикали, n — расстояние до направления градиента в гистограмме (имеется ввиду соответствующая гистограмма дескриптора, в которую вносит вклад этот градиент). За точку отсчета принимается левый нижний угол окна дескриптора и начальное значение гистограммы. За единичные отрезки берутся размеры регионов по горизонтали и вертикали для x и y соответственно, и количество градусов в компоненте гистограммы для n. Коэффициент трилинейной интерполяции определяется для каждой координаты (x, y, n) градиента как 1-d, где d равно расстоянию от координаты градиента до середины того единичного промежутка в который эта координата попала. Каждое вхождение градиента в гистограмму умножается на все три весовых коэффициента трилинейной интерполяции.
Дескриптор ключевой точки состоит из всех полученных гистограмм. Как уже было сказано размерность дескриптора на рисунке 32 компоненты (2x2x8), но на практике используются дескрипторы размерности 128 компонент (4x4x8).
Полученный дескриптор нормализуется, после чего все его компоненты, значение которых больше 0.2, урезаются до значения 0.2 и затем дескриптор нормализуется ещё раз. В таком виде дескрипторы готовы к использованию.
Последнее слово и литература
SIFT дескрипторы не лишены недостатков. Не все полученные точки и их дескрипторы будут отвечать предъявляемым требованиям. Естественно это будет сказываться на дальнейшем решении задачи сопоставления изображений. В некоторых случаях решение может быть не найдено, даже если оно существует. Например, при поиске аффинных преобразований (или фундаментальной матрицы) по двум изображениям кирпичной стены может быть не найдено решения из-за того, что стена состоит из повторяющихся объектов (кирпичей), которые делают похожими между собой дескрипторы разных ключевых точек. Несмотря на это обстоятельство, данные дескрипторы хорошо работают во многих практически важных случаях.
Плюс ко всему, этот метод запатентован.
В статье описана примерная схема работы алгоритма SIFT. Если вас заинтересовало почему этот алгоритм такой какой он есть и почему он работает, а так же обоснование выбора значений некоторых параметров, взятых в статье «с потолка» (например, число 0.2 в нормализации дескриптора), то вам следует обратиться к первоисточнику
David G. Lowe «Distinctive image features from scale-invariant keypoints»
Ещё одна статья, повторяющая основное содержание предыдущей. В ней подробней разобраны некоторые моменты
Yu Meng «Implementing the Scale Invariant Feature Transform(SIFT) Method»
