Комментарий к алгоритму выделения контуров Канни

Аннотация

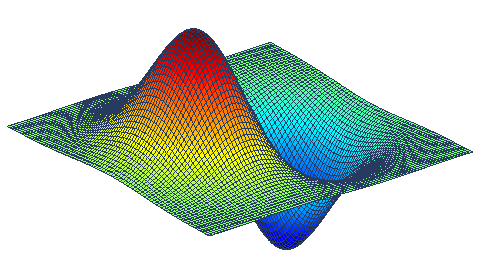
В статье Детектор границ Канни, как я уже и писал в комментариях к ней, искажена и потеряна суть алгоритма в том месте, где происходит поиск градиента. Для этого там используется ядра Собеля, о которых Канни совсем ничего не говорил. Я написал поправку, которая позволят алгоритму выделения контуров работать быстрее. Так же эту статью можно считать продолжением записи О градиенте изображения.
В статье не рассматриваются вопросы с выбором оптимального шага дискретизации ядра смаза.

Предпосылки

1. Прежде чем вычисляется градиент функции яркости изображения, часто, для получения устойчивого результата прибегают к фильтрации шумов с использованием Гауссова фильтра, то есть выполняют предварительный смаз.
2. Затем с использованием разностных аппроксимаций производных находят компоненты градиента.

Пусть смаз делается с использованием ядра размера NxN точек, а разностные шаблоны для вычисления производных вдоль осей имеют размеры 1xK и Kx1. Размер картинки положим равным MxM.
Для простоты будем считать только умножения, тогда последовательность «Смаз->Градиент» потребует N^2*M^2 + 2*K*M^2=(N^2 + 2*K)*M^2 операций.

Однако, известна формула

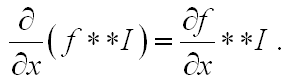
использование которой позволит нам сократить количество на порядки. О чем она говорит? — о том, что в принципе не обязательно вначале выполнять смаз а потом дифференцировать изображение. Можно продифференцировать ядро смаза f а потом уже выполнить свертку. Приступим.

Разделение ядра

Посмотрим на двумерную функцию Гаусса:

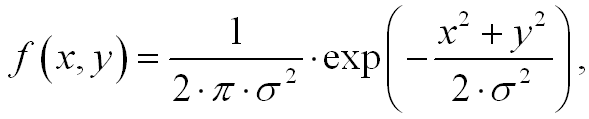
ее производная по x записывается в виде:

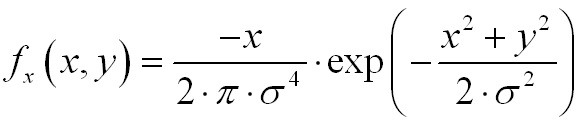
Получить эту замечательную производную мы можем исполнив код MatLab'a:

1. sigma = 1.4;
2. x = -3*sigma:0.1:3*sigma
3. y = x;
4. [x,y] = meshgrid(x,y);
5. Fx1 = ( -x/2/pi/sigma^2 ).*exp( -(x.^2+y.^2)/2/sigma^2 );
6. figure; surf(Fx1)

* This source code was highlighted with Source Code Highlighter.

Фильтр с таким ядром иногда называют фильтром Канни, а ядро — ядром Канни, который наравне с другими операторами, аппроксимирует производную. По этому поводу делюсь замечательно иллюстрированной заметкой.

Заметим, что производная разделима по координатам, а значит мы можем реализовать строчно — столбцовый алгоритм вычисления градиента смазанного изображения:

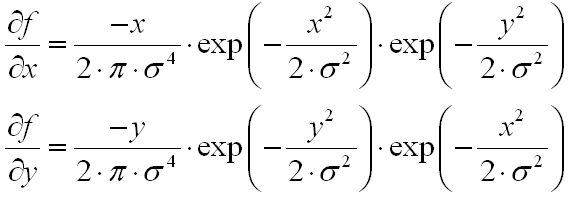
Посчитаем количество операций в случае строчно-столбцового алгоритма.

Для получения производной по y:

1. Обрабатываем Гауссом изображение I по строкам окном размера 1xK1, получаем изображение I1 за K*M^2 умножений (Не забудьте нормировать ядро),
2. Обрабатываем изображение I1 по строкам с ядром размера K1x1:
   
   
   
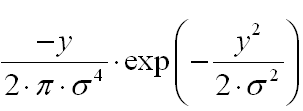
   (Не забудьте подобрать шаги дискретизации ядра так, чтобы сумма отсчетов была равна 0)
   На такую операцию нам понадобится столько же — K*M^2 умножений.
   

Алгоритм получения производной по x аналогичен, и суммируя количество операций получим, что для вычисления компонент смазанного градиента нам потребуется 4*K1*M^2.

Эффективность

Эффективность описанной оптимизации можно количественно выразить отношением:

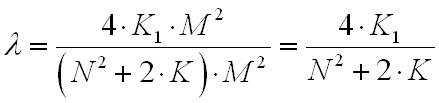
Получилось что эффективность зависит только от размеров окон, но не от размера изображений.
Пусть для смаза в простом алгоритме используется ядро размера N = 5, а для вычисления производных аппроксимация первого порядка ( ядра [-1 1] и [-1 1]' ) — K= 2.

В случае оптимизированного строчно-столбцового алгоритма положим K1 = 5. Тогда λ = 20/29 = 0.68.
Эффективность λ < 1 — у нас получилось сократить количество арифметических операций при вычислении последовательности «Смаз-Градиент».