В статье расскажу как можно очень быстро перечислить связные объекты на бинарном растре, значительно быстрее, чем я рассказывал в предыдущей статье. Казалось бы, куда такие скорости; теперь мы будем «расправляться» с картинками 4096 на 4096 за десятки миллисекунд. И хоть задача интересна и сама по себе, но в основе ее решения лежит довольно простой и оригинальный метод с достаточно широкой применимостью, основным тезисом которого является «сделаем как проще и посмотрим, что из этого выйдет». В данном случае в качестве основного вычислителя будет использоваться CUDA, но без особой специфики, потому что мы хотим сделать «очень просто». Задача
Необходимо выделить все связные объекты на бинарном растре (цвета пикселей — только черный и белый) и как-то их промаркировать. Для наглядности будем маркировать разными цветами. Само собой, соответствие «цвет — индекс объекта» достаточно тривиально. В нашем случае две точки являются связными, если они являются непосредственными соседями по вертикали или горизонтали (четырехсвязность), но алгоритм без труда можно модифицировать и для восьмисвязного случая (не это главное). Очень наглядно задача изложена в этой статье.
Для примера исходная картинка:
Алгоритм будет работать с очень большими картинками (до 16384x16384), но по понятным соображениям, в тексте статьи будут использованы уменьшенные изображения.
Исследовать или нет?
Довольно разумно, получая новую задачу, задуматься о том, какой метод ее решения был бы оптимален, какие ограничения могут возникнуть на пути решения, какова трудозатратность решения. Для того, чтобы быть объективным при выборе метода нужно рассмотреть много вариантов, иногда «слишком много», поэтому главное — правильно начать рассуждение, чтобы быстрее отсеять лишние варианты.
Худший «лучший случай»
Очевидно, что для решения задачи, нужно рассмотреть каждый пиксель изображения. Посмотрим, сколько времени будет выполняться модельный код на изображении размера 8192x8192:
for (int x = 0; x < dims[0]; x++)
{
for (int y = 0; y < dims[1]; y++)
{
image[x + dims[0]*y] = 0;
}
}
Да, его можно значительно «оптимизировать», свернув цикл в один, но любой разумный метод предполагает возможность доступа к отдельным пикселям изображения, так что индексация оставлена умышленно. Запустим его на каком-нибудь «средненьком» процессоре (в моем случае — Core 2 Duo E8400) и получим время работы около 680-780 мсек.
Пока сложно сказать, много это или мало, но кажется, что быстрее решить задачу не удастся.
Или так только кажется; ведь «все средства хороши» и есть технологии, значительно упрощающие решение задачи и дающие лучшие результаты; и в данном случае нам может сильно помочь технология CUDA, обладающая очень хорошими показателями для задач, интенсивно использующих память.
На моей средненькой видеокарте GTX460 мы получаем скорость доступа к видеопамяти порядка 40 Гбайт/с против 2 Гбайт/с для основной памяти. Такая скорость обработки достигается за счет использования массовой параллельности и достаточно быстрой памяти.
Разделяй и властвуй
Довольно нетривиальным может оказаться разделение задачи при учете специфики вычислений на видеокартах: нет стека, не очень быстрая синхронизация между потоками, невозможность строить сложные структуры данных.
Разумным способом разделения исходного изображения кажется деление его на небольшие «квадратики», каждый из которых будет обрабатываться отдельным потоком; это хорошо ложится в модель вычислений CUDA. А если опустить излишнюю специфику (что делается одним преобразованием):
UID = threadIdx.x + blockDim.x * blockIdx.xТо мы получим, что исходная задача представляется как объединение результатов выполнения подзадач для всех уникальных идентификаторов потоков (UID). Да, мы все еще не знаем, что именно будем делать, но уже знаем, как можно разбить задачу.
Вот так (буйство цветов — это авторская стилистика, а градиент показывает, что все UID разные) мы можем покрыть исходную картинку:
Каждый поток будет обрабатывать пиксели в пределах соответствующего блока, размером, например 32 x 32. Затем, возможно потребуется некоторая синхронизация и объединение результатов.
Проще простого
В математике часто используется один замечательный принцип: «если что-то нельзя, но очень хочется, то значит можно», по сути это просто «отодвигание» усложнений «на потом», но в данном случае оно нам очень пригодится.
Возьмем самый простой алгоритм заливки и в пределах каждого блока, применим его к соответствующим точкам (начиная с каждой еще не заполненной), не задумываясь о граничных эффектах вообще.
По сути, заполним точки изображения, находящиеся в блоке его уникальным идентификатором, результат предсказуем:
Пока мы начинали каждую новую итерацию заливки для того же UID тем же «цветом». Но в этом мало смысла — если уж мы не сможем обеспечить при таком подходе заполнение связных (на исходной картинке) областей одним цветом, то по крайней мере, сможет заполнить несвязные области разными «цветами». Поэтому каждую новую итерацию заливки будем выполнять с новым цветом, получаемым из UID и специальной добавки, гарантирующей уникальность этого цвета на общей картинке (достаточно прибавить общее количество потоков, умноженное на номер итерации).
Понять, что мы выиграли легче на картинке с «сеткой», обозначающей границы обрабатываемых квадратиков:
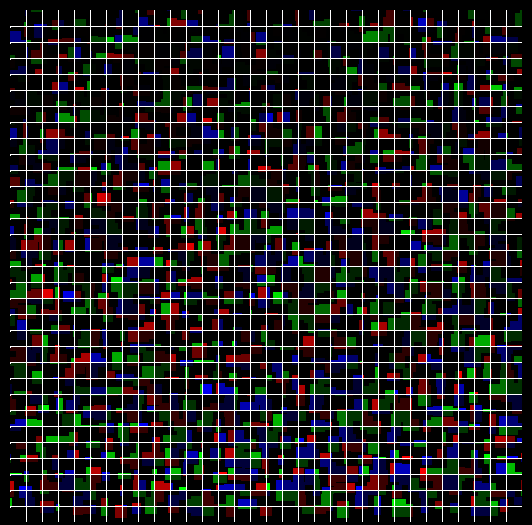
Теперь в пределах каждого квадратика связные области заполнены одним цветом, несвязные — разными. Работать это будет за O(n^3) (да, я выбрал худшую реализацию алгоритма заливки) для каждого квадратика, которых всего (imageSize.x / n) * (imageSize.y / n), бОльшая часть которых будет обработана одновременно при достаточном количестве потоков (обычно порядка 256).
Отложенные сложности
Осталось собрать результаты в один. Несмотря на то, что на уровне осознания это более сложно, чем применить классический метод для подзадач, алгоритмически это гораздо быстрее.
В действительности, мы хотим понять — какие разные цвета относятся к одной и той же связной области.
Для этого достаточно пройтись по пикселям сетки (именно той, что отрисована белым в иллюстрации) и проверить — являются ли непосредственными соседями пиксели разных цветов. Если являются — значит оба цвета обозначают в сущности один объект, который мы легко можем «перекрасить», или же держать этот факт «в уме» (обычно для получения параметров объектов этого достаточно).
Нехитрая арифметика приводит к тому, что количество пикселей сетки линейно зависит от периметра изображения — нам не нужно обрабатывать все точки внутри квадратиков, а нужна только их граница.
После прохода по этим точкам можно составить карту соответствия цветов (c1 == c2 == c3 ...) и аккуратно отрисовать результат:
Реализация и оценки скорости
Как ни удивительно, но «узкое место» данного метода — передача данных из основной памяти в видеопамять, здесь у нас нет альтернатив:
START_ACTION("Allocating GPU memory: image... ");
unsigned int* data_cuda;
cutilSafeCall( cudaMalloc((void **)&data_cuda, data_cuda_size) );
END_ACTION(data_cuda_size);
START_ACTION("Copying input data to GPU memory: image... ");
cutilSafeCall( cudaMemcpy(data_cuda, image, data_cuda_size, cudaMemcpyHostToDevice) );
END_ACTION(data_cuda_size);
Полученные 2 Гбайт/с ничем не удивляют — это скорость доступа к оперативной памяти. Для изображений, с которыми мы работаем — это миллисекунды, не страшно.
Вызов ядра (той функции, которая выполняется на видеокарте):
START_ACTION("Calling CUDA kernel... ");
cutilSafeCall( cudaThreadSynchronize() );
processKernelCUDA<<<GRID, THREADS>>>(data_cuda, dims[0], dims[1]);
cutilSafeCall( cudaThreadSynchronize() );
END_ACTION(data_cuda_size);
Вывод говорит за себя:
Calling CUDA kernel... 26.377720 msecs.
Throughput = 2.36942 GBytes/sПо сути, удалось реализовать выполнение всех подзадач, за время меньшее пересылки необходимых данных (изображения) в видеопамять. Это несмотря на то, что я выбрал худший алгоритм заливки, и сделал совершенно не оптимальную его реализацию. Имеет ли смысл что-то оптимизировать? Вам решать :)
Без кода ядра изложение, пожалуй, останется не полным, так что прошу любить и жаловать:
__global__ void processKernelCUDA(unsigned int* image, int dim_x, int dim_y)
{
// Full task size: image dimensions
int TASK_SIZE = dim_x * dim_y;
// Max UID for full task (really count of 'quads')
int MAX_UID = TASK_SIZE / QUAD_SIZE / QUAD_SIZE;
// calculate UID by CUDA implicit parameters; WORKERS = GRID*THREADS
for (int UID = threadIdx.x + blockDim.x * blockIdx.x; UID < MAX_UID; UID += WORKERS)
{
// count of quads for x-dimension
int quads_x = dim_x / QUAD_SIZE;
// current quad index form UID
int curr_quad_x = UID % quads_x;
int curr_quad_y = UID / quads_x;
// offset in global task
int offset = curr_quad_x * QUAD_SIZE + dim_x * curr_quad_y * QUAD_SIZE;
// id of 'color' to mark block, have to be >= 2
int COLOR_ID = 2 + UID;
do
{
// means that fill is not started yet
bool first_shot = true;
// process quad starting with specified 'offset'
bool done_something;
do // fill step
{
done_something = false;
for (int local_y = 0; local_y < QUAD_SIZE; local_y++) // step by y
{
// calcluate point index in whole image
int start_x = offset + local_y * dim_x;
for (int pos = start_x; pos < start_x + QUAD_SIZE; pos++) // step by x
{
if (image[pos] == 1) // is not marked with ID, is not blank
{
if ( first_shot /* start fill */ // else check neighbors:
|| image[pos-1] == COLOR_ID // x--
|| image[pos+1] == COLOR_ID // x++
|| local_y > 0 && image[pos-dim_x] == COLOR_ID // y--
|| local_y < QUAD_SIZE && image[pos+dim_x] == COLOR_ID ) // y++
{
image[pos] = COLOR_ID; // mark with ID
first_shot = false; // fill already started
done_something = true; // fill step does something
}
}
}
}
} while (done_something); // break if fill have no results
if (first_shot)
{
// no more work in this block, exit
break;
}
else
{
// next iteration: restart block with different color ID
COLOR_ID += MAX_UID;
}
} while(true);
}
}
На вход — указатель на картинку и разрешение картинки по X и по Y. Внутри вычисляется идентификатор подзадачи, выбирается смещение квадратика, соответствующего подзадаче, и он начинает заполняться нерекурсивным алгоритмом заливки.
Секрет успеха
Конечно не столь много задач, которые решаются за время, меньшее, времени получения данных для них, но в данном случае повезло. А кроме везения — правильный выбор технологии для решения и верный путь рассуждений, позволивший получить результат (вроде как) довольно серьезной задачи меньше чем за рабочий день.
P.S. Большая просьба, не копировать картинки и не делать ре-публикации без моего разрешения (автор метода я).
