Доброго времени суток, хабр! Сегодня я бы хотел рассказать про жадные алгоритмы.Есть много методов решения тех или иных задач: динамическое программирование, перебор. Не менее известными и довольно распространенными являются жадные алгоритмы.
Думаю, каждый программист в своей жизни хотя бы раз написал жадину, может быть, даже не задумываясь об этом. Что же это такое? Добро пожаловать под кат.
Жадность не порок
Итак, жадный алгоритм (greedy algorithm) — это алгоритм, который на каждом шагу делает локально наилучший выбор в надежде, что итоговое решение будет оптимальным.
К примеру, алгоритм Дейкстры нахождения кратчайшего пути в графе вполне себе жадный, потому что мы на каждом шагу ищем вершину с наименьшим весом, в которой мы еще не бывали, после чего обновляем значения других вершин. При этом можно доказать, что кратчайшие пути, найденные в вершинах, являются оптимальными.
К слову, алгоритм Флойда, который тоже ищет кратчайшие пути в графе (правда, между всеми вершинами), не является примером жадного алгоритма. Флойд демонстрирует другой метод — метод динамического программирования.
Использование жадного алгоритма довольно стандартное. Рассмотрим его на примере следующей задачи:
Задача о расписании
Пусть программисту-фрилансеру Васе Пупкину дано n заданий. У каждого задания известен свой дедлайн, а также его стоимость(то есть если он не выполняет это задание, то он теряет столько-то денег). Вася настолько крут, что за один день может сделать одно задание. Выполнение задания можно начать с момента 0. Нужно максимизировать прибыль.
Классический пример применения жадины: Васе выгодно делать самые «дорогие задания», а наименее дорогие можно и не выполнять — тогда прибыль будет максимальна. Возникает вопрос: каким образом распределить задания? Будем перебирать задания в порядке убывания стоимости и заполнять расписание следующим образом: если для заказа есть еще хотя бы одно свободное место в расписании раньше его дедлайна, то поставим его на самое последнее из таких мест, в противном случае в срок мы его не можем выполнить, значит поставим в конец из свободных мест.
Получается следующий код:
//tasks - массив заданий
Arrays.sort(tasks); //сортируем по убыванию стоимости
TreeSet<Integer> time = new TreeSet<Integer>();
for (int i = 1; i <= n; ++i) {
time.add(i);
}
int ans = 0;
for (int i = 0; i < n; ++i) {
Integer tmp = time.floor(tasks[i].time);
if (tmp == null) { // если нет свободного места в расписании, то в конец
time.remove(time.last());
} else { //иначе можно выполнить задание, добавляем в расписание
time.remove(tmp);
ans += tasks[i].cost;
}
}
Когда можно быть жадным?
Вывод:
Жизнь не матроид, жизнь — конечный автомат!
Как подсказывает википедия, матроид — это пара (X, I), где X — конечное множество, называемое носителем матроида, а I — некоторое множество подмножеств X, называемое семейством независимых множеств. При этом должны выполняться следующие условия:
-
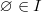
Множество I непусто. Даже если исходное множество X было пусто — X = Ø, то I будет состоять из одного элемента — множества, содержащего пустое. I = {{Ø}}
-
Любое подмножество любого элемента множества I также будет элементом этого множества.
-
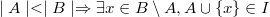
Если множества A и B принадлежат множеству I, а также известно, что размер А меньше B, то существует какой-нибудь элемент x из B, не принадлежащий А, такое что объединение x и A будет принадлежать множеству I. Это свойство является не совсем тривиальным, но чаще всего наиважшейшим из всех остальных.
Матроид называется взвешенным, если на множестве X существует аддитивная весовая функция w. Вес множества будет определяться как сумма весов его элементов.
Вернемся к
- первое свойство, очевидно, выполняется. Пустое множество выполненных заданий входит в наше множество. Ну и пофиг, что Вася не хочет зарабатывать деньги.
- второе множество тоже выполняется. Почему это так: давайте отсортируем успешно выполненные задания в порядке увеличения дедлайна. В таком порядке они все равно будут успешно выполненными. В таком порядке очевидно, что любое подмножество успешно выполненных заданий будет успешно выполнено.
- третье свойство, хоть и не очевидно, но выполняется. Пусть у нас есть два множества успешно выполненных заданий A и B, при чем известно, что |A| < |B|. Стандартно отсортируем задания в порядке увеличения дедлайна в обоих множествах. Возьмем задание из B, которого нет в A, и попробуем добавить его к множеству A. Это у нас получится, ведь если бы в А не было пробела, то данное задание должно было присутствовать.
К чему это я? Вся прелесть матроидов заключается в теореме Радо-Эдмондса: если доказать, что объект является матроидом, то жадный алгоритм будет работать корректно и выдавать правильный результат.
Сам по себе жадный алгоритм реализуется примерно вот так:
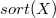//отсортируем по весу
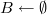//вначале ответом будет пустое множествоfor
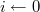to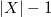 
if
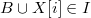then //если подходит
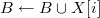//то включаем в множествоСписок литературы
PS
Кстати, задачу о расписаниях можно решить и быстрее за O(n). Кому не слабо? (Подсказка: нужно заменить TreeSet на другую структуру).
