Копаясь в дебрях LLVM, я неожиданно обнаружил для себя: насколько всё же интересная штука — оптимизация кода. Поэтому решил поделиться с вами своими наблюдениями в виде серии обзорных статей про оптимизации в компиляторах. В этих статьях я попытаюсь «разжевать» принципы работы оптимизаций и обязательно рассмотреть примеры.
Я попытаюсь выстроить оптимизации в порядке возрастания «сложности понимания», но это исключительно субъективно.
И ещё: некоторые названия и термины не являются устоявшимися и их используют «кто-как», поэтому я буду приводить несколько вариантов, но настоятельно рекомендую использовать именно англоязычные термины.
Прежде чем мы погрузимся в великолепные идеи и алгоритмы давайте немного поскучаем над теорией: разберёмся что такое оптимизации, для чего нужны и какими они бывают или не бывают.
Для начала дадим определение (из википедии):
Идём дальше: оптимизации бывают машинно-независимыми (высокоуровневыми) и машинно-зависимыми (низкоуровневыми). Смысл классификации понятен из названий, в машинно-зависимых оптимизациях используются особенности конретных архитектур, в высокоуровневых оптимизация происходит на уровне структуры кода.
Оптимизации также могут классифицироваться в зависимости от области их применения на локальные (оператор, последовательность операторов, базовый блок), внутрипроцедурные, межпроцедурные, внутримодульные и глобальные (оптимизация всей программы, «оптимизация при сборке», «Link-time optimization»).
Чую, что вы сейчас уснёте, давайте закончим на этом порцию теоиии и приступим уже к рассмотрению самих оптимизаций…
Самая простейшая, самая известная и самая распространённая оптимизация в компиляторах. Процесс «свёртки констант» включает в себя поиск выражений (или подвыражений), включающих ТОЛЬКО константы. Такие выражения вычисляются на этапе компиляции и в результирующем коде «сворачиваются» в вычисленное значение.
Рассмотрим пример (придуманный на ходу из головы, абсолютно синтетический, тривиальный, абстрактный, ничего не значащий, далёкий от реальности, etc… и все примеры будут такими):
Вроде бы получилось отлично и оптимизация выполнена, но на самом деле компиляторы поумнели и идут дальше. Дело в том, что в данном случае размер (
Олично… Несколько тактов процессора эта оптимизация нам определённо экономит.
Всё довольно просто, если наш код представлен в виде Абстрактного Синтаксического Дерева (AST). Тогда для нахождения числовых выражений и подвыражений достаточно искать узлы дерева одного уровня (то есть имеющие общего предка), содержащие только числовые значения. Тогда значение в вышестоящем узле (родительском) можно будет свернуть. Для наглядности рассмотрим на простом примере дерева для одного из выражений, возьмём наше
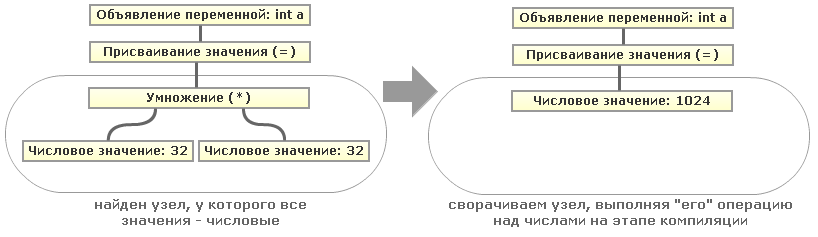
То есть рекурсивным обходом нашего дерева AST мы можем свернуть все подобные константные выражения. Кстати пример с числами опять же упрощён, вместо операций с числами вполне могут быть операции со строками (конкатенация) или операции со строками и числами (аналог python'овского "
Эта оптимизация обычно всегда описывается в комплекте с «Constant folding» (ведь они взаимодополняют друг друга), но это всё же отдельная оптимизация. Процесс «распространения констант» включает в поиск выражений, которые будут постоянными при любом возможном пути выполнения (до использования данного выражения) и их замену на эти значения. На деле всё проще, чем звучит — возьмём всё тот же пример, который мы уже использовали, но с учётом, что мы уже прошлись по нему оптимизацией «Constant folding»:
То есть в нашей изначальной программе вобщем-то не надо было делать никаких вычислений. А что произошло? Всё просто… Так как значения переменных
То есть компилятору необходимо для каждого выражения проверять, всегда ли его значение будет постоянным (а точнее — может ли оно измениться). Попробуем изобразить схематично:
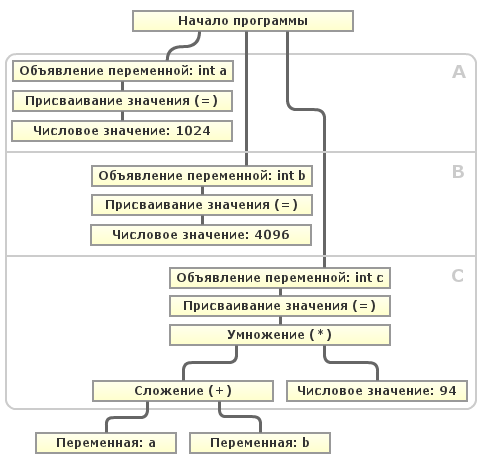
Допустим, что компилятор при очередном проходе оптимизации обнаруживает использование переменных
«Constant propagation» и «Constant folding» обычно прогоняются несколько раз, пока не перестанут вносить какие-либо изменения в код программы.
А это ещё один спутник двух предыдущих оптимизаций, практически брат-близнец «Constant Folding», выполняющий очень похожую работу, но позволяет избавится от лишних (промежуточных) присваиваний переменных, подменяя в выражениях промежуточные переменные. Гораздо нагляднее это будет на простейшем примере:
Очень простая, но, к сожаленью, мало чего улучшающая в плане производительности оптмизация. Всё просто: код, который никак не может быть использован в программе, можно удалить. Давайте посмотрим пару примеров «мёртвогогруза кода»:
Как видите, строка "
Думаю здесь тоже всё ясно без комментариев: строка "
Ну и последний пример для этой оптимизации:
И опять всё просто: функция sub не вызывается ни в одном месте программы, поэтому от неё можно избавиться.
С одной стороны «мёртвый код» в программе очень легко находится с помощью графа потока управления. Если в программе есть мертвый код, то граф будет либо несвязным и можно «выбросить» отдельные фрагменты графа. С другой стороны необходимо учитывать адресную арифметику и множество других ньюансов — не всегда можно однозначно определить, является ли код «мёртвым».
Очень полезная и «красивая» оптимизация. Заключается в следующем: если вы используете расчёт какого либо выражения два или более раз, то его можно рассчитать один раз, а затем подставить во все использующие его выражения. Ну и куда мы без примера:
Да, этот оптимизированный код выглядит гораздо страшнее и более громоздко, но он избавлен от «лишних вычислений» (однократно сложение и вычитание x и y вместо трёхкратных, однократное перемножение a и b вместно двухкратного). А теперь представьте сколько эта оптимизация экономит процессорного времени в рамках большой вычислительной программы.
P.S. На самом деле я хотел приводить схемки для каждой из оптимизаций, но извиняйте, меня хватило на рисование всего двух.
P.P.S. Подскажите УДОБНЫЙ сервис для рисования схемок и графов.
P.P.P.S. To be continued?
Я попытаюсь выстроить оптимизации в порядке возрастания «сложности понимания», но это исключительно субъективно.
И ещё: некоторые названия и термины не являются устоявшимися и их используют «кто-как», поэтому я буду приводить несколько вариантов, но настоятельно рекомендую использовать именно англоязычные термины.
Вступление
(совсем немного теории о типах оптимизаций, которую можно пропустить)
Прежде чем мы погрузимся в великолепные идеи и алгоритмы давайте немного поскучаем над теорией: разберёмся что такое оптимизации, для чего нужны и какими они бывают или не бывают.
Для начала дадим определение (из википедии):
Оптимизация программного кода — это модификация программ, выполняемая оптимизирующим компилятором или интерпретатором с целью улучшения их характеристик, таких как производительности или компактности, — без изменения функциональности.Последние три слова в этом определении очень важны: как бы не улучшала оптимизация характеристики программы, она обязательно должна сохранять изначальный смысл программы при любых условиях. Именно поэтому, например, в GCC существуют различные уровни оптимизации (настоятельно рекомендую сходить по этим ссылкам).
Идём дальше: оптимизации бывают машинно-независимыми (высокоуровневыми) и машинно-зависимыми (низкоуровневыми). Смысл классификации понятен из названий, в машинно-зависимых оптимизациях используются особенности конретных архитектур, в высокоуровневых оптимизация происходит на уровне структуры кода.
Оптимизации также могут классифицироваться в зависимости от области их применения на локальные (оператор, последовательность операторов, базовый блок), внутрипроцедурные, межпроцедурные, внутримодульные и глобальные (оптимизация всей программы, «оптимизация при сборке», «Link-time optimization»).
Чую, что вы сейчас уснёте, давайте закончим на этом порцию теоиии и приступим уже к рассмотрению самих оптимизаций…
Constant folding
(Свёртывание/Свёртка констант)
Самая простейшая, самая известная и самая распространённая оптимизация в компиляторах. Процесс «свёртки констант» включает в себя поиск выражений (или подвыражений), включающих ТОЛЬКО константы. Такие выражения вычисляются на этапе компиляции и в результирующем коде «сворачиваются» в вычисленное значение.
Рассмотрим пример (придуманный на ходу из головы, абсолютно синтетический, тривиальный, абстрактный, ничего не значащий, далёкий от реальности, etc… и все примеры будут такими):
| До оптимизации | После оптимизации |
|---|---|
|
|
sizeof) структуры "p" тоже является константой, и компиляторы об этом знают, поэтому получаем:| Разворачиваем sizeof | Завершаем свертывание |
|---|---|
|
|
Всё довольно просто, если наш код представлен в виде Абстрактного Синтаксического Дерева (AST). Тогда для нахождения числовых выражений и подвыражений достаточно искать узлы дерева одного уровня (то есть имеющие общего предка), содержащие только числовые значения. Тогда значение в вышестоящем узле (родительском) можно будет свернуть. Для наглядности рассмотрим на простом примере дерева для одного из выражений, возьмём наше
"int a = 32*32;":
То есть рекурсивным обходом нашего дерева AST мы можем свернуть все подобные константные выражения. Кстати пример с числами опять же упрощён, вместо операций с числами вполне могут быть операции со строками (конкатенация) или операции со строками и числами (аналог python'овского "
'-' * 10") или константами любых других типов данных, поддерживаемых исходным языком программирования.Constant propagation
(Распространение констант)
Эта оптимизация обычно всегда описывается в комплекте с «Constant folding» (ведь они взаимодополняют друг друга), но это всё же отдельная оптимизация. Процесс «распространения констант» включает в поиск выражений, которые будут постоянными при любом возможном пути выполнения (до использования данного выражения) и их замену на эти значения. На деле всё проще, чем звучит — возьмём всё тот же пример, который мы уже использовали, но с учётом, что мы уже прошлись по нему оптимизацией «Constant folding»:
| До оптимизации | После оптимизации |
|---|---|
|
|
"a" и "b" никак не могут измениться между их объявлением и использованием в вычислении значения "c", то компилятор сам может подставить их значения в выражение и вычислить его. То есть компилятору необходимо для каждого выражения проверять, всегда ли его значение будет постоянным (а точнее — может ли оно измениться). Попробуем изобразить схематично:

Допустим, что компилятор при очередном проходе оптимизации обнаруживает использование переменных
"a" и "b". Как видно из схемы, после объявления переменной "a" в блоке A и переменной "b" в блоке B, ни одна, ни другая переменная не могут изменить значение в последующих блоках (A,B,C) перед их использованием. Этот случай тривиален, так как вся программа линейна и представляет из себя так называемый Базовый блок (BB). Но алгоритм определения «изменяемости» переменной в базовом блоке это ещё далеко не всё. Программа может включать условные конструкции, циклы, безусловные переходы и т.д. Тогда для определения «изменяемости» переменной необходимо построить направленный граф с базовыми блоками в вершинах, рёбра — передача управления между базовыми блоками. Такой граф называется Графом потока управления (CFG) и применяется для осуществления многих оптимизаций. В таком графе можно определить все базовые блоки, которые необходимо пройти от инициализации переменной до её использования и определить для каждого блока, может ли в нём измениться значение переменной. В случае невозможности его изменения, компилятор легко может заменить её значение константой. «Constant propagation» и «Constant folding» обычно прогоняются несколько раз, пока не перестанут вносить какие-либо изменения в код программы.
Copy propagation
(Распространение копий)
А это ещё один спутник двух предыдущих оптимизаций, практически брат-близнец «Constant Folding», выполняющий очень похожую работу, но позволяет избавится от лишних (промежуточных) присваиваний переменных, подменяя в выражениях промежуточные переменные. Гораздо нагляднее это будет на простейшем примере:
| До оптимизации | После оптимизации |
|---|---|
|
|
Dead Code Elimination (DCE)
(Устранение/Исключение недоступного кода)
Очень простая, но, к сожаленью, мало чего улучшающая в плане производительности оптмизация. Всё просто: код, который никак не может быть использован в программе, можно удалить. Давайте посмотрим пару примеров «мёртвого
| До оптимизации | После оптимизации |
|---|---|
|
|
printf("Hi, I'm dead code =( !");" является недостижимой при любых обстоятельствах: либо программа выполняется бесконечно, либо завершается «насильно». Давайте ещё пару примеров:| До оптимизации | После оптимизации |
|---|---|
|
|
printf("x = %d \n", &x);" также, как и в предыдущем примере, недостижима при любом пути исполнения программы, а объявленная в первой строки функции main переменная y никак не используется.Ну и последний пример для этой оптимизации:
| До оптимизации | После оптимизации |
|---|---|
|
|
С одной стороны «мёртвый код» в программе очень легко находится с помощью графа потока управления. Если в программе есть мертвый код, то граф будет либо несвязным и можно «выбросить» отдельные фрагменты графа. С другой стороны необходимо учитывать адресную арифметику и множество других ньюансов — не всегда можно однозначно определить, является ли код «мёртвым».
Common Sub-Expression Elimination (CSE)
(Устранение общих подвыражений)
Очень полезная и «красивая» оптимизация. Заключается в следующем: если вы используете расчёт какого либо выражения два или более раз, то его можно рассчитать один раз, а затем подставить во все использующие его выражения. Ну и куда мы без примера:
| До оптимизации | После оптимизации |
|---|---|
|
|
P.S. На самом деле я хотел приводить схемки для каждой из оптимизаций, но извиняйте, меня хватило на рисование всего двух.
P.P.S. Подскажите УДОБНЫЙ сервис для рисования схемок и графов.
P.P.P.S. To be continued?
