Играя в эту замечательную игру, я заметил, что мой мозг полностью отключен т.к. игра не требует умственной деятельности, соответственно мне стало скучно. Я с нетерпением ждал когда-же эта игра закончиться и решил приблизительно прикинуть сколько-же еще ходов понадобиться? Без компьютера конечно-же не получилось и тогда я решил, что нужно обязатяльно провести несколько сотен тысяч испытаний, посчитать мат. ожидание, дисперсию и по возможности узнать тип распределения. Вооружившись с++, qt и чашкой кофе я перешел к делу…
Колода карт тщательно перетосовывается и раздается поровну двум игрокам (по 18 карт). Игроки одновременно вытягивают верхнюю карту и у кого она выше — забирает обе, при этом шестерка считается выше туза. В случаее если карты равны, оба игрока вытягивают еще по одной карте (если такова присутствует) и кладут их в закрытую, после чего вытягивают в открытую еще по одной и сравнивают их, у кого больше — забирает все, если опять равны — алгоритм разрешения спора выполняется еще одну итерацию.
Важно чтобы карты со стола забирались под низ колоды и при этом также перетасовывались (чтобы исключить возможность циклов).
В ходе реализации программы, я пытался максимально абстрагироваться от карт, обозвал карты от шестерки до туза числами от 0 до 8, полностью игнорировал масти. Результат испытаний сильно зависит от качества раздачи — от того насколько карты в колодах игроков случайны). Однако даже тщательная перетосовка не гарантирует абсолютной случайности, вот и я в программе не стал ничего изобретать, а просто тысячу раз поменя�� местами случайно выбранные карты из колоды:
Алгоритм заключается в том, что оба игрока, пока у каждого есть карты, повторяют итерацию игры, которая заключается в том, что пока у кого-то есть карты на руках и есть конфликты (обе карты равны; еще не сделан ход), игроки, по возможности, скидывают 1-2 карты и, оценивая их номинал, решают кому достаются все сброшенные на стол карты…

На графике отображена плотность распределения вероятностей случайной величины количества необходимых ходов для завершения игры.
За 100 секунд мой E8400 в одном потоке провел 1 000 000 испытаний. График меня сильно удивил, выходит, что чаще всего игры заканчиваются за 25 ходов. А бывает и меньше… Но увидев результаты вычисления мат. ожидания и дисперсии, я успокоился, все нормально:
Мат ожидание: Mx = 255.054;
Дисперсия: Dx = 319726.545;
Итого, судя по мат. ожиданию, если беретесь играть в эту игру — рассчитывайте минут на 30. А судя по дисперсии, если беретесь играть в эту игру — даже не думайте на что-то рассчитывать).
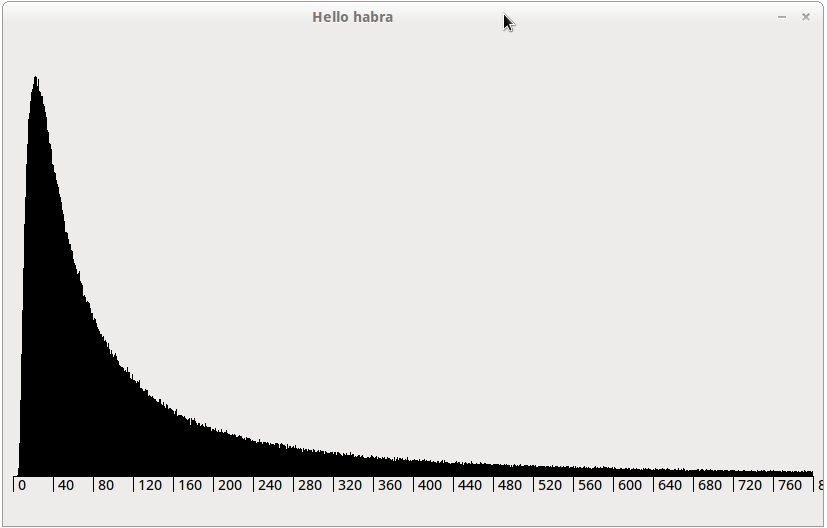
Чуть более детальный график плотности.

«Увеличения» «основной части».

LN(f) по просьбе OLS
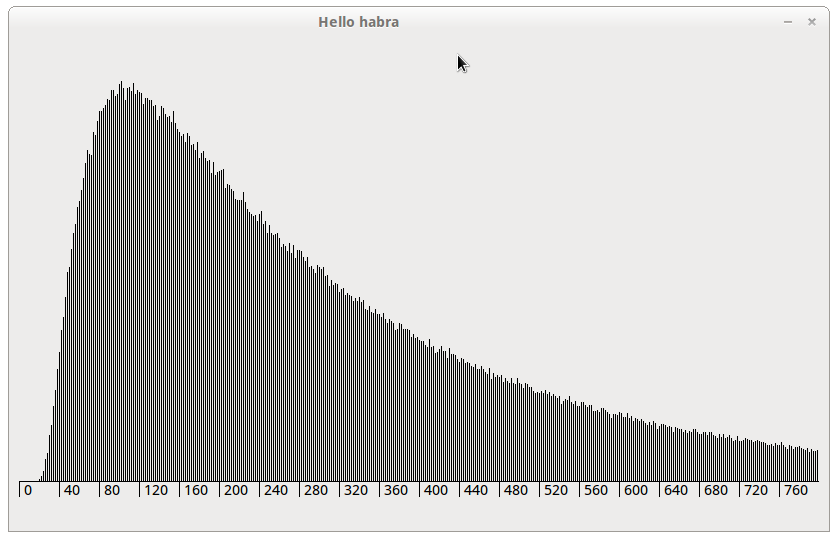
Для непрерывного варианта игры (карты — числа от 0..1), разница только в параметрах распределения и том, что f(x) = 0 для всех непарных х. Сделано по просьбе Bodigrim
Еще несколько свойств:
Медиана: 90;
Мода: 25;
Доверительный интервал: 80% — от 6 до 316.
Приношу свои извинения, в коде обнаружено несколько досадных ошибок, которые сильно искажают результат. Это обновление перепроверенно n раз, проверить корректность проведения испытаний можно тут, тут и тут.

Итоговый результат:
Мат. ожидание: 187;
Дисперсия: 23044;
Медиана: 142;
Мода: 62.
На графике можно увидеть2 независимых графика, что парные числа имеют большую частоту. Это можно объяснить тем, что независимо от того сколько (1, 3, 5...), кто и когда забирает карт, число с1 + с2 — парное.
с1 — количество сделаных ходов.
с2 — количество карт у любого из игроков (у каждого одновременно либо парное либо непарное количество карт).
Одна и только одна ситуация приводит игру к завершению с непарным количеством ходов — когда один из игроков отбирает парное количество карт, чем и завершает игру. Такое может произойти только в конце игры, пример.
Еще раз извиняюсь; за указание на ошибки благодарим Catalysis
Правила игры
Колода карт тщательно перетосовывается и раздается поровну двум игрокам (по 18 карт). Игроки одновременно вытягивают верхнюю карту и у кого она выше — забирает обе, при этом шестерка считается выше туза. В случаее если карты равны, оба игрока вытягивают еще по одной карте (если такова присутствует) и кладут их в закрытую, после чего вытягивают в открытую еще по одной и сравнивают их, у кого больше — забирает все, если опять равны — алгоритм разрешения спора выполняется еще одну итерацию.
Важно чтобы карты со стола забирались под низ колоды и при этом также перетасовывались (чтобы исключить возможность циклов).
Раздача карт
В ходе реализации программы, я пытался максимально абстрагироваться от карт, обозвал карты от шестерки до туза числами от 0 до 8, полностью игнорировал масти. Результат испытаний сильно зависит от качества раздачи — от того насколько карты в колодах игроков случайны). Однако даже тщательная перетосовка не гарантирует абсолютной случайности, вот и я в программе не стал ничего изобретать, а просто тысячу раз поменя�� местами случайно выбранные карты из колоды:
void generateMap(QList* player1, QList* player2)
{
int a[36];
for (int i = 0; i < 36; i++)
a[i] = i / 4;
int temp, i1, i2;
for (int i = 0; i < 1000; i++)
{
i1 = random() % 36;
i2 = random() % 36;
temp = a[i1];
a[i1] = a[i2];
a[i2] = temp;
}
for (int i = 0; i < 18; i++)
{
player1->append(a[i]);
player2->append(a[i+18]);
}
}
Игровой процесс
Алгоритм заключается в том, что оба игрока, пока у каждого есть карты, повторяют итерацию игры, которая заключается в том, что пока у кого-то есть карты на руках и есть конфликты (обе карты равны; еще не сделан ход), игроки, по возможности, скидывают 1-2 карты и, оценивая их номинал, решают кому достаются все сброшенные на стол карты…
int Process(QList* player1, QList* player2)
{
QList* temp = new QList();
int p1, p2, k;
int counter = 0;
while ((player1->count() > 0) && (player2->count() > 0))
{
p1 = -1; p2 = -1;
while ((p1 == p2) && ((player1->count() > 0) || (player2->count() > 0)))
{
for (int i = 0; i < 1 + (p1 >= 0); i++)
if (player1->count() > 0) {
p1 = player1->first();
temp->append(p1);
player1->removeFirst();
}
for (int i = 0; i < 1 + (p2 >= 0); i++)
if (player2->count() > 0) {
p2 = player2->first();
temp->append(player2->first());
player2->removeFirst();
}
}
QList* winner;
if ((p1 > p2) || ((p1 == 0) && (p2 == 8))) {
winner = player1;
} else {
winner = player2;
}
while (!temp->isEmpty())
{
k = random() % temp->count();
winner->append(temp->at(k));
temp->removeAt(k);
}
temp->clear(); counter++;
if (counter > 100000) player1->clear();
}
delete temp;
return counter;
}
Отображение результата

На графике отображена плотность распределения вероятностей случайной величины количества необходимых ходов для завершения игры.
void CChart::paintEvent(QPaintEvent *){
QPainter painter(this);
for (int i = 0; i < 21; i++) {
painter.drawText(QRect(i*40+15,450,30,20),QString::number(i*25));
painter.drawLine(10+i*40, 465, 10+i*40,450);
}
for (int i = 0; i < 100; i++){
int h = this->counts[i] * 400 / this->max;
painter.drawRect(10 + i*8, 450-h, 4, h);
}
}
Выводы
За 100 секунд мой E8400 в одном потоке провел 1 000 000 испытаний. График меня сильно удивил, выходит, что чаще всего игры заканчиваются за 25 ходов. А бывает и меньше… Но увидев результаты вычисления мат. ожидания и дисперсии, я успокоился, все нормально:
Мат ожидание: Mx = 255.054;
Дисперсия: Dx = 319726.545;
Итого, судя по мат. ожиданию, если беретесь играть в эту игру — рассчитывайте минут на 30. А судя по дисперсии, если беретесь играть в эту игру — даже не думайте на что-то рассчитывать).
Обновление

Чуть более детальный график плотности.

«Увеличения» «основной части».

LN(f) по просьбе OLS

Для непрерывного варианта игры (карты — числа от 0..1), разница только в параметрах распределения и том, что f(x) = 0 для всех непарных х. Сделано по просьбе Bodigrim
Еще несколько свойств:
Медиана: 90;
Мода: 25;
Доверительный интервал: 80% — от 6 до 316.
Обновление 2
Приношу свои извинения, в коде обнаружено несколько досадных ошибок, которые сильно искажают результат. Это обновление перепроверенно n раз, проверить корректность проведения испытаний можно тут, тут и тут.

Итоговый результат:
Мат. ожидание: 187;
Дисперсия: 23044;
Медиана: 142;
Мода: 62.
На графике можно увидеть
с1 — количество сделаных ходов.
с2 — количество карт у любого из игроков (у каждого одновременно либо парное либо непарное количество карт).
Одна и только одна ситуация приводит игру к завершению с непарным количеством ходов — когда один из игроков отбирает парное количество карт, чем и завершает игру. Такое может произойти только в конце игры, пример.
Еще раз извиняюсь; за указание на ошибки благодарим Catalysis
