В настоящей статье я хотел бы сделать обзор популярных алгоритмов для решения задачи нахождения максимальной общей подпоследовательности или LCS (longest common sequense). Так как акцент сделан на обучении, а не на реальном использовании, в качестве языка для реализации выбран Python, что позволит сократить количество кода и сконцентрироваться на основных идеях.
Последовательность представляет собой упорядоченный набор элементов. Строка — это частный случай последовательности, дальнейшие примеры будут для простоты рассматривать именно строки, но без изменений их можно использовать и для произвольного текста или чего-нибудь последовательного еще.
Пусть имеется последовательность x, состоящая из элементов x1x2...xm и последовательность y, состоящая из элементов y1y2...yn. z — подпоследовательность x в том случае, если существует строго возрастающий набор индексов элементов x, из которых получается z.
Общей подпоследовательностью для x и y считаем такую последовательность z, которая является одновременно подпоследовательностью x и подпоследовательностью y.
Максимальная общая подпоследовательность — это общая подпоследовательность с максимальной длинной. Далее по тексту будем использовать сокращение LCS.
В качестве примера, пусть x=HABRAHABR, y=HARBOUR, в этом случае LCS(x, y)=HARBR. Можно уже переходить непосредственно к алгоритму вычисления LCS, но, хорошо бы понять, для чего нам может это может понадобиться.
Наиболее частое применение — использование в программах для сравнения файлов, например GNU diff. Имея найденную для двух текстов LCS, составить список элементарных изменений для превращения x в y или обратно задача тривиальная. В качестве бонуса, на основе длины общей подпоследовательности можно задать метрику для определения схожести двух последовательностей. Все, теперь точно можно переходить к делу.
Для начала пара наблюдений:
Этих наб��юдений уже достаточно, чтобы реализовать рекурсию:
Теперь можно подумать, что с этой реализацией не так. В наихудшем случае, когда между x и y нет одинаковых элементов LCS_RECURSIVE вызовется 2len(x)+len(y) раз, при уровне рекурсии len(x)+len(y). Даже если закрыть глаза на производительность, код:
без дополнительного вызова sys.setrecursionlimit удачно не выполнится. Не самая удачная реализация.
Рассматриваемый алгоритм также известен как алгоритм Нидлмана—Вунша (Needleman-Wunsch).
Весь подход сводится к поэтапному заполнению матрицы, где строки представляют собой элементы x, а колонки элементы y. При заполнении действуют два правила, вытекающие из уже сделанных наблюдений:
1. Если элемент xi равен yj то в ячейке (i,j) записывается значение ячейки (i-1,j-1) с добавлением единицы
2. Если элемент xi не равен yj то в ячейку (i,j) записывается максимум из значений(i-1,j) и (i,j-1).
Заполнение происходит в двойном цикле по i и j с увеличением значений на единицу, таким образом на каждой итерации нужные на этом шаге значения ячеек уже вычислены:
Иллюстрация происходящего:

Ячейки, в которых непосредственно происходило увеличение значения подсвечены. После заполнения матрицы, соединив эти ячейки, мы получим искомый LCS. Соединять при этом нужно двигаясь от максимальных индексов к минимальным, если ячейка подсвечена, то добавляем соответствующий элемент к LCS, если нет, то двигаемся вверх или влево в зависимости от того где находится большее значение в матрице:
Сложность алогоритма — O(len(x)*len(y)), такая же оценка по памяти. Таким образом, если я захочу построчно сравнить два файла из 100000 строк, то нужно будет хранить в памяти матрицу из 1010 элементов. Т.е. реальное использование грозит получением MemoryError почти на ровном месте. Перед тем как перейти к следующему алгоритму заметим, что при заполнении матрицы L на каждой итерации по элементам x нам нужна только строка, полученная на предыщем ходу. Т.е. если бы задача ограничивалась только нахождением длины LCS без необходимости вычисления самой LCS, то можно было бы снизить использование памяти до O(len(y)), сохраняя одновременно только две строки матрицы L.
Идея в основе этого алгоритма проста: если разделить входную последовательность x=x1x2...xm на две произвольные части по любому граничному индексу i на xb=x1x2...xi и xe=xi+1xi+2...xm, то найдется способ аналогичного разбиения y (найдется такой индекс j, разбивающий y на yb=y1y2...yj и ye=yj+1yj+2...yn), такой, что LCS(x,y) = LCS(xb,yb) + LCS(xe,ye).
Для того, чтобы найти это разбиение y предлагается:
Это можно представить, как заполнение матрицы L с двух противоположных концов:
Заметим, что раз есть необходимость только в последней строке матрицы L, то при вычислении хранить всю матрицу не нужно. Немного изменив реализацию fill_dyn_matrix получим:
Теперь непосредственно, о самом алгоритме. Он представляет собой классический divide and conquer: пока в последовательности x есть элементы, мы делим x пополам, находим подходящее разбиение для y и возвращаем сумму рекурсивных вызовов для пар последовательностей (xb,yb) и (xe,ye). Заметим, что в тривиальном случае, если x состоит из одного элемента �� встречается в y мы просто возвращаем последовательность из этого единственного элемента x.
Теперь требования по памяти у нас O(len(y)), время, необходимое для вычисления, удвоилось, но асимптотически по-прежнему O(len(x)len(y)).
Первое что нам потребуется это создание хэш таблицы matchlist, которая будет содержать индексы элементов второй последовательностей. Время необходимое для этого O(len(y)). Следующий код на питоне делает это:
Для последовательности «HARBOUR» хэш будет следующим {'A': [1], 'B': [3], 'H': [0], 'O': [4], 'R': [2, 6], 'U': [5]}.
Далее, перебирая элементы последовательности x, заполняем массив THRESH соответсвующими индексами из заготовленного matchlist, таким образом, что значением k-го элемента THRESH должен быть индекс y_index, при условии что THRESH[k-1] < y_index и y_index < THRESH[k]. Таким образом, в любой момент времени массив THRESH отсортирован и для нахождения подходящего k мы можем использовать бинарный поиск. При обновлении элемента THRESH мы также добавляем соответствующий индексу y_index элемент последовательности к нашей LCS. Внести ясность может следующий код:
После этого нам остается только собрать из LINK_x саму последовательность.
Время работы этого алгоритма равно O((r + n) log n), где n — длина большей последовательности, а r — количество совпадений, в худшем случае при r = n*n, мы получаем время работы хуже чем в предыдущем варианте решения. Требования по памяти остаются порядка O(r+n).
Алгоритмов решающих данную проблему довольно много, асимптотически, самый эффективный алгоритм (Masek and Paterson) имеет оценку по времени O(n*n/log n). Учитывая общую небольшую эффективность при вычислениях LCS, на практике перед работой алгоритма выполняются простейшие подготовки, вроде отбрасывания одинаковых элементов в начале и в конце последовательностей и поиск тривиальных отличий между последовательностями. Также, существуют некоторые оптимизации с использованием битовых операций, не влияющие на асимптотику времени работы.
скачать весь код с примерами
Определения
Последовательность представляет собой упорядоченный набор элементов. Строка — это частный случай последовательности, дальнейшие примеры будут для простоты рассматривать именно строки, но без изменений их можно использовать и для произвольного текста или чего-нибудь последовательного еще.
Пусть имеется последовательность x, состоящая из элементов x1x2...xm и последовательность y, состоящая из элементов y1y2...yn. z — подпоследовательность x в том случае, если существует строго возрастающий набор индексов элементов x, из которых получается z.
Общей подпоследовательностью для x и y считаем такую последовательность z, которая является одновременно подпоследовательностью x и подпоследовательностью y.
Максимальная общая подпоследовательность — это общая подпоследовательность с максимальной длинной. Далее по тексту будем использовать сокращение LCS.
В качестве примера, пусть x=HABRAHABR, y=HARBOUR, в этом случае LCS(x, y)=HARBR. Можно уже переходить непосредственно к алгоритму вычисления LCS, но, хорошо бы понять, для чего нам может это может понадобиться.
Применение на практике
Наиболее частое применение — использование в программах для сравнения файлов, например GNU diff. Имея найденную для двух текстов LCS, составить список элементарных изменений для превращения x в y или обратно задача тривиальная. В качестве бонуса, на основе длины общей подпоследовательности можно задать метрику для определения схожести двух последовательностей. Все, теперь точно можно переходить к делу.
Первый подход или народное творчество
Для начала пара наблюдений:
- Если для последовательностей x и y нами уже вычислена LCS(x, y)=z, то, LCS для последовательностей полученных из x и y путем добавления одинакового элемента, будет состоять из z и этого добавленного элемента
- Если мы добавим к последовательностям x и y по одному разному элементу, то для полученных таким образом xa и yb, LCS должна быть большая из двух: LCS(x,yb) или LCS(xa,y)
Этих наб��юдений уже достаточно, чтобы реализовать рекурсию:
def LCS_RECURSIVE(x, y): if len(x) == 0 or len(y) == 0: return [] if x[-1] == y[-1]: return LCS_RECURSIVE(x[:-1], y[:-1]) + [x[-1]] else: left = LCS_RECURSIVE(x[:-1], y) right = LCS_RECURSIVE(x, y[:-1]) return left if len(left) > len(right) else right
Теперь можно подумать, что с этой реализацией не так. В наихудшем случае, когда между x и y нет одинаковых элементов LCS_RECURSIVE вызовется 2len(x)+len(y) раз, при уровне рекурсии len(x)+len(y). Даже если закрыть глаза на производительность, код:
from uuid import uuid4 x = [uuid4().hex for _ in xrange(500)] y = [uuid4().hex for _ in xrange(500)] print LCS_RECURSIVE(x,y)
без дополнительного вызова sys.setrecursionlimit удачно не выполнится. Не самая удачная реализация.
Динамическое программирование или 64 кб хватит всем
Рассматриваемый алгоритм также известен как алгоритм Нидлмана—Вунша (Needleman-Wunsch).
Весь подход сводится к поэтапному заполнению матрицы, где строки представляют собой элементы x, а колонки элементы y. При заполнении действуют два правила, вытекающие из уже сделанных наблюдений:
1. Если элемент xi равен yj то в ячейке (i,j) записывается значение ячейки (i-1,j-1) с добавлением единицы
2. Если элемент xi не равен yj то в ячейку (i,j) записывается максимум из значений(i-1,j) и (i,j-1).
Заполнение происходит в двойном цикле по i и j с увеличением значений на единицу, таким образом на каждой итерации нужные на этом шаге значения ячеек уже вычислены:
def fill_dyn_matrix(x, y): L = [[0]*(len(y)+1) for _ in xrange(len(x)+1)] for x_i,x_elem in enumerate(x): for y_i,y_elem in enumerate(y): if x_elem == y_elem: L[x_i][y_i] = L[x_i-1][y_i-1] + 1 else: L[x_i][y_i] = max((L[x_i][y_i-1],L[x_i-1][y_i])) return L
Иллюстрация происходящего:

Ячейки, в которых непосредственно происходило увеличение значения подсвечены. После заполнения матрицы, соединив эти ячейки, мы получим искомый LCS. Соединять при этом нужно двигаясь от максимальных индексов к минимальным, если ячейка подсвечена, то добавляем соответствующий элемент к LCS, если нет, то двигаемся вверх или влево в зависимости от того где находится большее значение в матрице:
def LCS_DYN(x, y): L = fill_dyn_matrix(x, y) LCS = [] x_i,y_i = len(x)-1,len(y)-1 while x_i >= 0 and y_i >= 0: if x[x_i] == y[y_i]: LCS.append(x[x_i]) x_i, y_i = x_i-1, y_i-1 elif L[x_i-1][y_i] > L[x_i][y_i-1]: x_i -= 1 else: y_i -= 1 LCS.reverse() return LCS
Сложность алогоритма — O(len(x)*len(y)), такая же оценка по памяти. Таким образом, если я захочу построчно сравнить два файла из 100000 строк, то нужно будет хранить в памяти матрицу из 1010 элементов. Т.е. реальное использование грозит получением MemoryError почти на ровном месте. Перед тем как перейти к следующему алгоритму заметим, что при заполнении матрицы L на каждой итерации по элементам x нам нужна только строка, полученная на предыщем ходу. Т.е. если бы задача ограничивалась только нахождением длины LCS без необходимости вычисления самой LCS, то можно было бы снизить использование памяти до O(len(y)), сохраняя одновременно только две строки матрицы L.
Борьба за место или Алгоритм Хишберга (Hirschberg)
Идея в основе этого алгоритма проста: если разделить входную последовательность x=x1x2...xm на две произвольные части по любому граничному индексу i на xb=x1x2...xi и xe=xi+1xi+2...xm, то найдется способ аналогичного разбиения y (найдется такой индекс j, разбивающий y на yb=y1y2...yj и ye=yj+1yj+2...yn), такой, что LCS(x,y) = LCS(xb,yb) + LCS(xe,ye).
Для того, чтобы найти это разбиение y предлагается:
- Заполнить динамическую матрицу L с помощью fill_dyn_matrix для xs и y. L1 приравняем последней строке вычисленной матрицы L
- Заполнить матрицу L для *xe и *y (обратные последовательности для xe и y, в терминах Python: list(reversed(x)), list(reversed(y))). Приравняем *L2 последнюю строку вычисленной матрицы L, L2 это риверс от *L2
- Принять j равным индексу, для которого сумма L1[j]+L2[j] максимальна
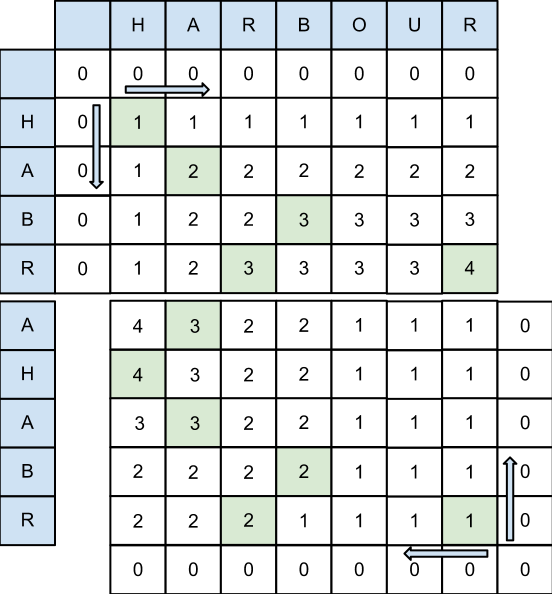
Это можно представить, как заполнение матрицы L с двух противоположных концов:

Заметим, что раз есть необходимость только в последней строке матрицы L, то при вычислении хранить всю матрицу не нужно. Немного изменив реализацию fill_dyn_matrix получим:
def lcs_length(x, y): curr = [0]*(1 + len(y)) for x_elem in x: prev = curr[:] for y_i, y_elem in enumerate(y): if x_elem == y_elem: curr[y_i + 1] = prev[y_i] + 1 else: curr[y_i + 1] = max(curr[y_i], prev[y_i + 1]) return curr
Теперь непосредственно, о самом алгоритме. Он представляет собой классический divide and conquer: пока в последовательности x есть элементы, мы делим x пополам, находим подходящее разбиение для y и возвращаем сумму рекурсивных вызовов для пар последовательностей (xb,yb) и (xe,ye). Заметим, что в тривиальном случае, если x состоит из одного элемента �� встречается в y мы просто возвращаем последовательность из этого единственного элемента x.
def LCS_HIRSHBERG(x, y): x_len = len(x) if x_len == 0: return [] elif x_len == 1: if x[0] in y: return [x[0]] else: return [] else: i = x_len // 2 xb, xe = x[:i], x[i:] L1 = lcs_length(xb, y) L2 = reversed(lcs_length(xe[::-1], y[::-1])) SUM = (l1 + l2 for l1,l2 in itertools.izip(L1, L2)) _, j = max((sum_val, sum_i) for sum_i, sum_val in enumerate(SUM)) yb, ye = y[:j], y[j:] return LCS_HIRSHBERG(xb, yb) + LCS_HIRSHBERG(xe, ye)
Теперь требования по памяти у нас O(len(y)), время, необходимое для вычисления, удвоилось, но асимптотически по-прежнему O(len(x)len(y)).
Алгоритм Ханта-Шуманского (Hunt-Szymanski Algorithm)
Первое что нам потребуется это создание хэш таблицы matchlist, которая будет содержать индексы элементов второй последовательностей. Время необходимое для этого O(len(y)). Следующий код на питоне делает это:
y_matchlist = {} for index, elem in enumerate(y): indexes = y_matchlist.setdefault(elem, []) indexes.append(index) y_matchlist[elem] = indexes
Для последовательности «HARBOUR» хэш будет следующим {'A': [1], 'B': [3], 'H': [0], 'O': [4], 'R': [2, 6], 'U': [5]}.
Далее, перебирая элементы последовательности x, заполняем массив THRESH соответсвующими индексами из заготовленного matchlist, таким образом, что значением k-го элемента THRESH должен быть индекс y_index, при условии что THRESH[k-1] < y_index и y_index < THRESH[k]. Таким образом, в любой момент времени массив THRESH отсортирован и для нахождения подходящего k мы можем использовать бинарный поиск. При обновлении элемента THRESH мы также добавляем соответствующий индексу y_index элемент последовательности к нашей LCS. Внести ясность может следующий код:
x_length, y_length = len(x), len(y) min_length = min(x_length, y_length) THRESH = list(itertools.repeat(y_length, min_length+1)) LINK_s1 = list(itertools.repeat(None, min_length+1)) LINK_s2 = list(itertools.repeat(None, min_length+1)) THRESH[0], t = -1, 0 for x_index,x_elem in enumerate(x): y_indexes = y_matchlist.get(x_elem, []) for y_index in reversed(y_indexes): k_start = bisect.bisect_left(THRESH, y_index, 1, t) k_end = bisect.bisect_right(THRESH, y_index, k_start, t) for k in xrange(k_start, k_end+2): if THRESH[k-1] < y_index and y_index < THRESH[k]: THRESH[k] = y_index LINK_x[k] = (x_index, LINK_x[k-1]) if k > t: t = k
После этого нам остается только собрать из LINK_x саму последовательность.
Время работы этого алгоритма равно O((r + n) log n), где n — длина большей последовательности, а r — количество совпадений, в худшем случае при r = n*n, мы получаем время работы хуже чем в предыдущем варианте решения. Требования по памяти остаются порядка O(r+n).
Итого
Алгоритмов решающих данную проблему довольно много, асимптотически, самый эффективный алгоритм (Masek and Paterson) имеет оценку по времени O(n*n/log n). Учитывая общую небольшую эффективность при вычислениях LCS, на практике перед работой алгоритма выполняются простейшие подготовки, вроде отбрасывания одинаковых элементов в начале и в конце последовательностей и поиск тривиальных отличий между последовательностями. Также, существуют некоторые оптимизации с использованием битовых операций, не влияющие на асимптотику времени работы.
скачать весь код с примерами
