Не так давно я увлёкся игрой в сёги. К сожалению, эта чудесная игра практически не известна в России, поэтому пока я не научил играть друзей, мне приходилось играть с программой. Конечно, мне было интересно, как эта программа работает.
Ниже представлен небольшой рассказ о компьютерных алгоритмах, используемых в интеллектуальных играх.
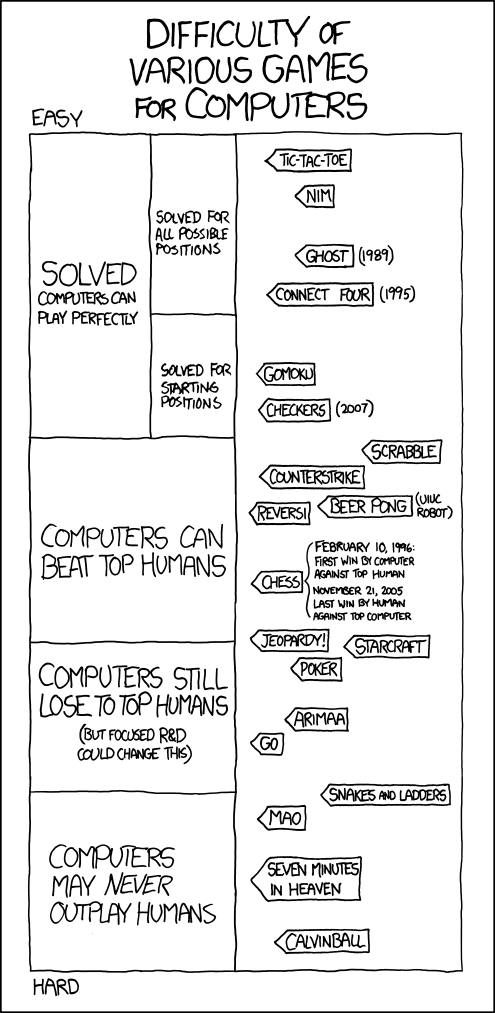
Рассмотрение алгоритмов мы начнём с одной из самых простых игр: с крестиков-ноликов. Уверен, почти все из вас умеют играть так, чтобы никогда не проигрывать, но давайте посмотрим, как это удаётся компьютеру.
Практически все игры можно представить в виде т.н. деревьев решений, где каждый узел будет представлять собой один шаг решения задачи (ход в игре), ветвь в дереве соответствует решению, которое ведёт к более полному решению, листы представляют собой окончательное решение (итоговые позиции). Наша цель – найти в дереве лучший путь от корня до листа.
Деревья решений обычно невероятно велики. Для рассматриваемой нами игры в крестики-нолики дерево содержит более полумиллиона узлов. Понятно, что в шашках, шахматах, а тем более сёгах и го, деревья на порядок больше.
Но, тем не менее, на примере детской игры можно рассмотреть методы, позволяющие находить оптимальные решения в очень больших деревьях.
Если у игрока есть n возможных ходов, то соответствующий узел будет иметь n ветвей (потомков). Например, в крестиках-ноликах корневой узел соответствует пустому полю. Первый игрок может поставить крестик на любой из 9 квадратиков. Каждому возможному ходу будет соответствовать ветвь, исходящая из корневого узла. Когда игрок поставил крестик, второй игрок может поставить нолик в любом из оставшихся восьми квадратов. Каждому из этих ходов соответствует ветвь, исходящая из узла, представляющего текущую позицию крестика на доске. На рисунке показан небольшой фрагмент исследуемого дерева.
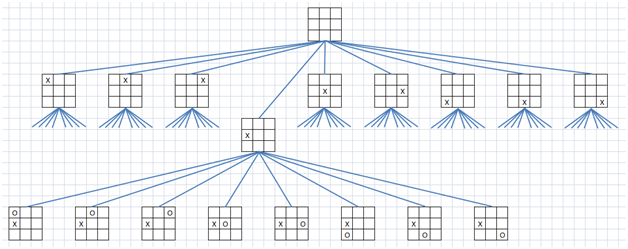
Как можно видеть из рисунка, дерево игры растёт чрезвычайно быстро. Если дерево продолжит расти таким образом, то во всём дереве будет содержаться 9!=362880 листьев.
На самом деле многие возможные узлы в дереве игры запрещены правилами. Например, если один из игроков уже выиграл, то построение дерева на этом этапе можно завершить. Удаление всех невозможных узлов сократит дерево до четверти миллиона листов. Но это всё ещё очень и очень большое дерево и полный его обход займёт непозволительно много времени. Для более сложных игр деревья имеют просто невообразимый размер. Если бы в шахматах на каждом шаге у игрока было бы 16 возможных ходов, то в дереве было бы более триллиона узлов после пяти ходов.
Чтобы выполнить поиск в игровом дереве, нужно иметь возможность определить значение позиции игрового поля. В крестиках-ноликах для первого игрока большое значение имеют позиции, в которых три крестика расположены в ряд, так как при этом первый игрок выигрывает. Значение игрока, который ставит нолик, в этих позициях поля очень мало, потому что при этом он проигрывает.
Каждому игроку можно назначить четыре значения для конкретной позиции на поле:
• 4 – выигрыш;
• 3 – не ясная ситуация;
• 2 – ничья;
• 1 – проигрыш;
Для исчерпывающего исследования игрового дерева можно использовать стратегию минимакса. При этом мы будем пытаться минимизировать максимальное значение, которое может иметь позиция для противника после следующего хода. Сначала определяется максимальное значение, которое может набрать противник после каждого из ваших возможных ходов. Затем выбирается ход, при котором противник получает минимальное значение.
Процедура, поиска оптимального хода, вычисляет значение позиции поля. Эта процедура исследует каждый возможный ход. Для каждого хода она рекурсивно вызывает себя, чтобы определить значение которое будет иметь позиция противника. Затем она выбирает ход, который даёт противнику минимальное значение. Рекурсивное обращение процедуры к себе будет продолжаться, пока не наступит одно из трёх возможных событий. Во-первых, может быть найдена позиция, в которой игрок побеждает. В этом случае процедура устанавливает значение позиции поля в 4. В случае если игрок проигрывает, то значение поля будет установлено в 1. Во-вторых, может быть найдена позиция, в которой ни один игрок не может сделать ход. Игра заканчивается ничьей, поэтому процедура устанавливает значение позиции в 2. И, наконец, процедура может достичь заранее установленной глубины рекурсии. Если она превышает допустимую глубину, то значение поля устанавливается в 3, указывая на неопределённый исход. Максимальная глубина рекурсии предохраняет программу от слишком большой траты времени. Это особенно важно для сложных игр, вроде шахмат, где поиск может продолжаться практически бесконечно долго. Максимальная глубина рекурсии также позволяет задавать уровень мастерства. Чем глубже программа может исследовать дерево, тем лучше будут её ходы.
На рисунке показано дерево игры в конце партии. Первый и третий ходы приводят к победе игрока, играющего ноликами, поэтому эти ходы имеют для него значение 4. Второй возможный ход приводит к ничьей и имеет значение 2. Программа выбирает второй ход, потому что он даёт игроку ноликов самое маленькое значение поля.

Если бы минимаксный алгоритм был бы единственным инструментом для исследования игровых деревьев, то перебор больших деревьев был бы довольно сложным. К счастью существует несколько приёмов, которые можно использовать для поиска в больших деревьях.
Во-первых, можно запомнить несколько первых ходов, выбранных экспертами игры. Если выбрать первый ход за программу, то дерево поиска будет сокращено в 9 раз. Фактически, программа не должна перебирать дерево, пока противник не сделал ход. В этом случае и компьютер, и его противник уже выбрали ветви, поэтому дерево будет содержать всего 7!=5040 ветвей.
Использование дополнительной памяти для хранения нескольких ходов значительно сокращает время, необходимое для поиска в дереве.
Другой способ улучшить поиск – указать важные шаблоны. В шахматах такими шаблонами могут быть позиции, угрожающие нескольким фигурам сразу, королю или ферзю. В случае если шахматная программа замечает шаблон обмена, она может временно изменить глубину рекурсии, чтобы просмотреть серию обменов до конца и решить будет ли обмен выгодным. Если обмен всё же происходит, количество оставшихся фигур становится меньше и поиск в дереве упрощается.
И, наконец, в более сложных случаях необходимо использовать эвристики. Например, в шахматах обычной эвристикой является усиление преимущества. Когда у противника меньше сильных фигур и одинаковое с вами число слабых фигур, то следует идти на обмен при любой возможности.
Полностью перебрать дерево в крестиках-ноликах может даже школьник. В шашках число возможных позиций оценивается числом 1020. Это очень и очень много, но в 2007 году суперкомпьютер сумел просчитать все возможные ходы. Т.е., начиная с 2007 года, человек не может (даже теоретически) выиграть у компьютера.
С шахматами полный перебор едва ли возможен в ближайшем будущем. Число всех возможных позиций в шахматах оценива��тся числом 1046. Это число настолько велико, что даже суперкомпьютеру потребуется астрономическое время, чтобы перебрать эти позиции. Тем не менее, в шахматах есть определённый прогресс. Пусть перебрать все позиции и невозможно, но весьма эффективными оказываются эвристики и базы позиций. Если вы когда-нибудь учились играть в шахматы, то вам наверняка рассказывали о королевском, ферзевом гамбите, защите Филидора или староиндийской защите. Все эти дебюты применяются в начале партии. Всё дело в том, что они уже давно и достаточно глубоко (вплоть до 20 хода) просчитаны. Эндшпили в шахматах тоже весьма хорошо просчитаны. Стоит только поискать в интернете по запросам: «эндшпиль ладья против лёгкой фигуры», «эндшпиль две ладьи против ферзя» и т.д., чтобы убедиться в этом. Получается, что просчитывать необходимо только середину партию, а там, как сказано выше, весьма эффективны эвристики.
В середине 1990-х были созданы программы, способные победить чемпиона мира. Яркий пример – матч Deep Blue – Kasparov. Если в 1996 году Каспаров проиграл только одну партию, но выиграл матч, то уже в 1997 году Deep Blue победила Каспарова не в отдельной партии, а во всём матче.
Основное отличие сёги от шахмат в том, что взятые фигуры не покидают игру, а могут в любой момент вернуться на любую клетку поля. Эта особенность вместе с большим размером поля и большим набором фигур, делают сёги невероятно сложной игрой. Число партий резко возрастает до числа 10226, эвристика обмена (самая распространённая) становится полностью неэффективной, так, как обмены только усложняют игру, базу партий для сёги построить тоже практически невозможно, учитывая их количество.
Подавляющее большинство программ используют описанную выше стратегию минимакса и основное отличие в программах — это алгоритм оценки позиции и эвристики. Сейчас матчи между программами и профессионалами запрещены, чтобы не умалять достоинство профессиональных игроков, но время от времени ассоциация сёги даёт разрешение на матчи. Самое большое достижении ИИ в этой игре — победа над сильнейшей из женщин. Итиё Симидзу играла против программы Akara. Строго говоря, Akara — это не одна программа, а 4 независимых движка. Решение о лучше ходе принимается простым голосованием. Не смотря на значительный прогресс в области ИИ в сёги программы пока не способны выиграть у сильнейшего игрока.
Ещё интереснее обстоят дела в игре го. Число итоговых позиций в го 10171, это исключает прямой перебор всех вариантов.
К сожалению, минимаксное дерево поиска тоже работает весьма плохо. Дело в том, что в го число возможных позиций растёт очень быстро и даже суперкомпьютеры не могут перебирать ходы с достаточной скоростью. Лучшие программы способны «заглянуть в будущее» на 12 ходов. Полученные позиции оцениваются, и выбираются лучшие варианты. Для этих вариантов программа начинает снова анализировать игру вглубь, пытаясь выбрать самый лучший вариант. И так несколько раз. Одна из особенностей го в том, что в этой игре стратегическое мышление гораздо важнее тактического. И даже, если программа добивается локального тактического преимущества, настоящий мастер всё равно выигрывает.
Тем не менее программисты нашли очень оригинальный алгоритм, который позволяет программам играть на уровне профессионалов (о победе над сильнейшими игроками, как и в сёгах пока нет и речи).
Основная идея заключается в использовании алгоритма поиска в дереве Монте-Карло. Из названия понятно, что это рандомизированный алгоритм. Как же он используется в го? Программа перебирают случайным образом несколько миллионов игр, которые могут быть сыграны из текущего положения. Причём каждая игру проигрывается до конца, программу вычисляет выгодность хода, единственно ограничение — следование правилам.
Проиграв до конца миллионы партий, программа получает некоторую статистику о вероятности выигрыша после первого хода. По этой статистике программа решает, что такой-то ход приведёт к выигрышу с вероятностью в 5%, такой-то — 3% и так далее. Далее программа просто выбирает ход с наибольшей вероятностью выигрыша и повторяет алгоритм. В итоге программа делает ход, который с наибольшей вероятностью ведёт к победе.
Использование этого метода позволило программе выиграть у сильнейшего игрока, правда с форой в 7 камней.
Неужели рано или поздно наступит момент, когда программы начнут выигрывать у людей в 100% игр? Конечно нет, у нас же всегда есть бутылочка!
Ниже представлен небольшой рассказ о компьютерных алгоритмах, используемых в интеллектуальных играх.

Рассмотрение алгоритмов мы начнём с одной из самых простых игр: с крестиков-ноликов. Уверен, почти все из вас умеют играть так, чтобы никогда не проигрывать, но давайте посмотрим, как это удаётся компьютеру.
Практически все игры можно представить в виде т.н. деревьев решений, где каждый узел будет представлять собой один шаг решения задачи (ход в игре), ветвь в дереве соответствует решению, которое ведёт к более полному решению, листы представляют собой окончательное решение (итоговые позиции). Наша цель – найти в дереве лучший путь от корня до листа.
Деревья решений обычно невероятно велики. Для рассматриваемой нами игры в крестики-нолики дерево содержит более полумиллиона узлов. Понятно, что в шашках, шахматах, а тем более сёгах и го, деревья на порядок больше.
Но, тем не менее, на примере детской игры можно рассмотреть методы, позволяющие находить оптимальные решения в очень больших деревьях.
Если у игрока есть n возможных ходов, то соответствующий узел будет иметь n ветвей (потомков). Например, в крестиках-ноликах корневой узел соответствует пустому полю. Первый игрок может поставить крестик на любой из 9 квадратиков. Каждому возможному ходу будет соответствовать ветвь, исходящая из корневого узла. Когда игрок поставил крестик, второй игрок может поставить нолик в любом из оставшихся восьми квадратов. Каждому из этих ходов соответствует ветвь, исходящая из узла, представляющего текущую позицию крестика на доске. На рисунке показан небольшой фрагмент исследуемого дерева.

Как можно видеть из рисунка, дерево игры растёт чрезвычайно быстро. Если дерево продолжит расти таким образом, то во всём дереве будет содержаться 9!=362880 листьев.
На самом деле многие возможные узлы в дереве игры запрещены правилами. Например, если один из игроков уже выиграл, то построение дерева на этом этапе можно завершить. Удаление всех невозможных узлов сократит дерево до четверти миллиона листов. Но это всё ещё очень и очень большое дерево и полный его обход займёт непозволительно много времени. Для более сложных игр деревья имеют просто невообразимый размер. Если бы в шахматах на каждом шаге у игрока было бы 16 возможных ходов, то в дереве было бы более триллиона узлов после пяти ходов.
Чтобы выполнить поиск в игровом дереве, нужно иметь возможность определить значение позиции игрового поля. В крестиках-ноликах для первого игрока большое значение имеют позиции, в которых три крестика расположены в ряд, так как при этом первый игрок выигрывает. Значение игрока, который ставит нолик, в этих позициях поля очень мало, потому что при этом он проигрывает.
Каждому игроку можно назначить четыре значения для конкретной позиции на поле:
• 4 – выигрыш;
• 3 – не ясная ситуация;
• 2 – ничья;
• 1 – проигрыш;
Для исчерпывающего исследования игрового дерева можно использовать стратегию минимакса. При этом мы будем пытаться минимизировать максимальное значение, которое может иметь позиция для противника после следующего хода. Сначала определяется максимальное значение, которое может набрать противник после каждого из ваших возможных ходов. Затем выбирается ход, при котором противник получает минимальное значение.
Процедура, поиска оптимального хода, вычисляет значение позиции поля. Эта процедура исследует каждый возможный ход. Для каждого хода она рекурсивно вызывает себя, чтобы определить значение которое будет иметь позиция противника. Затем она выбирает ход, который даёт противнику минимальное значение. Рекурсивное обращение процедуры к себе будет продолжаться, пока не наступит одно из трёх возможных событий. Во-первых, может быть найдена позиция, в которой игрок побеждает. В этом случае процедура устанавливает значение позиции поля в 4. В случае если игрок проигрывает, то значение поля будет установлено в 1. Во-вторых, может быть найдена позиция, в которой ни один игрок не может сделать ход. Игра заканчивается ничьей, поэтому процедура устанавливает значение позиции в 2. И, наконец, процедура может достичь заранее установленной глубины рекурсии. Если она превышает допустимую глубину, то значение поля устанавливается в 3, указывая на неопределённый исход. Максимальная глубина рекурсии предохраняет программу от слишком большой траты времени. Это особенно важно для сложных игр, вроде шахмат, где поиск может продолжаться практически бесконечно долго. Максимальная глубина рекурсии также позволяет задавать уровень мастерства. Чем глубже программа может исследовать дерево, тем лучше будут её ходы.
На рисунке показано дерево игры в конце партии. Первый и третий ходы приводят к победе игрока, играющего ноликами, поэтому эти ходы имеют для него значение 4. Второй возможный ход приводит к ничьей и имеет значение 2. Программа выбирает второй ход, потому что он даёт игроку ноликов самое маленькое значение поля.

Если бы минимаксный алгоритм был бы единственным инструментом для исследования игровых деревьев, то перебор больших деревьев был бы довольно сложным. К счастью существует несколько приёмов, которые можно использовать для поиска в больших деревьях.
Во-первых, можно запомнить несколько первых ходов, выбранных экспертами игры. Если выбрать первый ход за программу, то дерево поиска будет сокращено в 9 раз. Фактически, программа не должна перебирать дерево, пока противник не сделал ход. В этом случае и компьютер, и его противник уже выбрали ветви, поэтому дерево будет содержать всего 7!=5040 ветвей.
Использование дополнительной памяти для хранения нескольких ходов значительно сокращает время, необходимое для поиска в дереве.
Другой способ улучшить поиск – указать важные шаблоны. В шахматах такими шаблонами могут быть позиции, угрожающие нескольким фигурам сразу, королю или ферзю. В случае если шахматная программа замечает шаблон обмена, она может временно изменить глубину рекурсии, чтобы просмотреть серию обменов до конца и решить будет ли обмен выгодным. Если обмен всё же происходит, количество оставшихся фигур становится меньше и поиск в дереве упрощается.
И, наконец, в более сложных случаях необходимо использовать эвристики. Например, в шахматах обычной эвристикой является усиление преимущества. Когда у противника меньше сильных фигур и одинаковое с вами число слабых фигур, то следует идти на обмен при любой возможности.
Как же обстоят дела в реальности (шашки и шахматы)
Полностью перебрать дерево в крестиках-ноликах может даже школьник. В шашках число возможных позиций оценивается числом 1020. Это очень и очень много, но в 2007 году суперкомпьютер сумел просчитать все возможные ходы. Т.е., начиная с 2007 года, человек не может (даже теоретически) выиграть у компьютера.
С шахматами полный перебор едва ли возможен в ближайшем будущем. Число всех возможных позиций в шахматах оценива��тся числом 1046. Это число настолько велико, что даже суперкомпьютеру потребуется астрономическое время, чтобы перебрать эти позиции. Тем не менее, в шахматах есть определённый прогресс. Пусть перебрать все позиции и невозможно, но весьма эффективными оказываются эвристики и базы позиций. Если вы когда-нибудь учились играть в шахматы, то вам наверняка рассказывали о королевском, ферзевом гамбите, защите Филидора или староиндийской защите. Все эти дебюты применяются в начале партии. Всё дело в том, что они уже давно и достаточно глубоко (вплоть до 20 хода) просчитаны. Эндшпили в шахматах тоже весьма хорошо просчитаны. Стоит только поискать в интернете по запросам: «эндшпиль ладья против лёгкой фигуры», «эндшпиль две ладьи против ферзя» и т.д., чтобы убедиться в этом. Получается, что просчитывать необходимо только середину партию, а там, как сказано выше, весьма эффективны эвристики.
В середине 1990-х были созданы программы, способные победить чемпиона мира. Яркий пример – матч Deep Blue – Kasparov. Если в 1996 году Каспаров проиграл только одну партию, но выиграл матч, то уже в 1997 году Deep Blue победила Каспарова не в отдельной партии, а во всём матче.
Как же обстоят дела в реальности (сёги и го)
Основное отличие сёги от шахмат в том, что взятые фигуры не покидают игру, а могут в любой момент вернуться на любую клетку поля. Эта особенность вместе с большим размером поля и большим набором фигур, делают сёги невероятно сложной игрой. Число партий резко возрастает до числа 10226, эвристика обмена (самая распространённая) становится полностью неэффективной, так, как обмены только усложняют игру, базу партий для сёги построить тоже практически невозможно, учитывая их количество.
Подавляющее большинство программ используют описанную выше стратегию минимакса и основное отличие в программах — это алгоритм оценки позиции и эвристики. Сейчас матчи между программами и профессионалами запрещены, чтобы не умалять достоинство профессиональных игроков, но время от времени ассоциация сёги даёт разрешение на матчи. Самое большое достижении ИИ в этой игре — победа над сильнейшей из женщин. Итиё Симидзу играла против программы Akara. Строго говоря, Akara — это не одна программа, а 4 независимых движка. Решение о лучше ходе принимается простым голосованием. Не смотря на значительный прогресс в области ИИ в сёги программы пока не способны выиграть у сильнейшего игрока.
Ещё интереснее обстоят дела в игре го. Число итоговых позиций в го 10171, это исключает прямой перебор всех вариантов.
К сожалению, минимаксное дерево поиска тоже работает весьма плохо. Дело в том, что в го число возможных позиций растёт очень быстро и даже суперкомпьютеры не могут перебирать ходы с достаточной скоростью. Лучшие программы способны «заглянуть в будущее» на 12 ходов. Полученные позиции оцениваются, и выбираются лучшие варианты. Для этих вариантов программа начинает снова анализировать игру вглубь, пытаясь выбрать самый лучший вариант. И так несколько раз. Одна из особенностей го в том, что в этой игре стратегическое мышление гораздо важнее тактического. И даже, если программа добивается локального тактического преимущества, настоящий мастер всё равно выигрывает.
Тем не менее программисты нашли очень оригинальный алгоритм, который позволяет программам играть на уровне профессионалов (о победе над сильнейшими игроками, как и в сёгах пока нет и речи).
Основная идея заключается в использовании алгоритма поиска в дереве Монте-Карло. Из названия понятно, что это рандомизированный алгоритм. Как же он используется в го? Программа перебирают случайным образом несколько миллионов игр, которые могут быть сыграны из текущего положения. Причём каждая игру проигрывается до конца, программу вычисляет выгодность хода, единственно ограничение — следование правилам.
Проиграв до конца миллионы партий, программа получает некоторую статистику о вероятности выигрыша после первого хода. По этой статистике программа решает, что такой-то ход приведёт к выигрышу с вероятностью в 5%, такой-то — 3% и так далее. Далее программа просто выбирает ход с наибольшей вероятностью выигрыша и повторяет алгоритм. В итоге программа делает ход, который с наибольшей вероятностью ведёт к победе.
Использование этого метода позволило программе выиграть у сильнейшего игрока, правда с форой в 7 камней.
Неужели рано или поздно наступит момент, когда программы начнут выигрывать у людей в 100% игр? Конечно нет, у нас же всегда есть бутылочка!
