Этот пост поможет вам выкрутиться из довольно-таки щекотливой ситуации. Скажем, вы заперты в комнате, у вас есть моток ниток и иголка, и от вас настойчиво требуют посчитать приблизительное значение числа Пи, используя лишь эти предметы, ну, всякое бывает, знаете. Так вот, сегодня слушая на курсере курс по матану Пенсильванского университета, я вдруг узнал, как это сделать. Вот чего я и предположить не мог, так это того, что число Пи скрывается и тут. Оказалось, что корни этого вопроса уходят аж в 18 век, когда Жорж-Луи Леклерк де Бюффон поставил себе следующую задачу: «предположим, пол сделан из деревянных полосок двух цветов, они чередуются; какова вероятность того, что брошенная иголка упадет так, что будет пересекать линию состыковки двух полосок?» Симуляцию этого процесса и ответ на вопрос можно найти под катом.Симуляция
Чтобы не портить интригу, начнем, пожалуй, с эксперимента. Итак, у нас имеется множество иголок длины L и моток ниток зеленого цвета. Нанесем на поверхность некоторое количество параллельных отрезков одинаковой длины на расстоянии L друг от друга.
Кинем на это поле 100 иголок.
Пожалуй, мало. Добавим еще 900 и отметим те иголки, которые пересекают нити, красным цветом.
Предположим, мы кидали не все иголки разом, а по одной, и записывали на каждом шаге отношение количества иголок, попавших на нити, к общему количеству брошенных иголок, тем самым получая все большее и большее приближение вероятности того, что иголка, падая, пересечет нить.
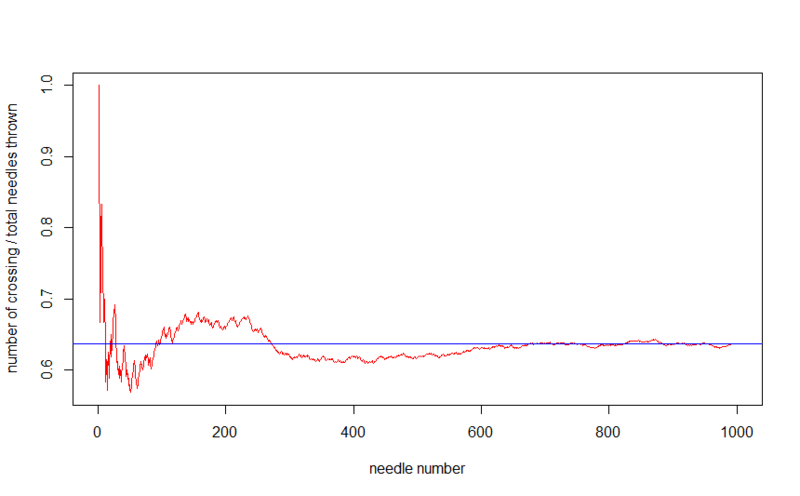
Если бросить 10000 иголок, то картина будет более точной.
А теперь сделаем следующее преобразование: разделим двойку на каждое число полученного ряда.
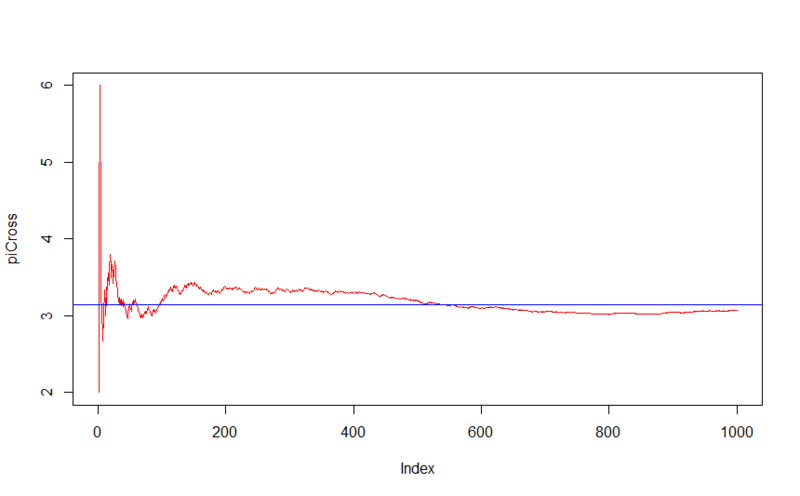
Для 10000 иголок уже точнее.
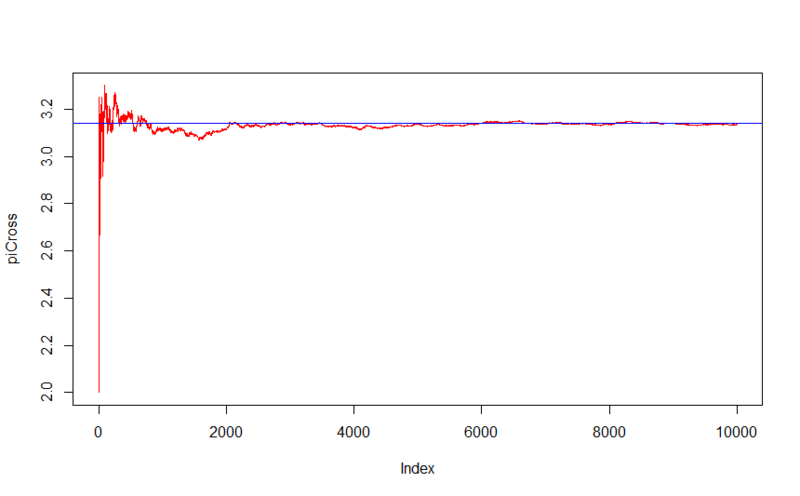
Если найти среднее из последних пяти тысяч членов ряда мы получим 3.141685, в то время как число пи равно 3.141593.
В общем, ни для кого уже не секрет, что последний ряд сходится к числу Пи. Но как такое могло произойти? Я узнал об этом на 28 году жизни из вышеупомянутого курса. Окунемся в матан.
Теория
Будем рассматривать иголку и ближайшую от нее линию справа. Расстояние от левого конца иглы обозначим h, угол отклонения от линии — a.
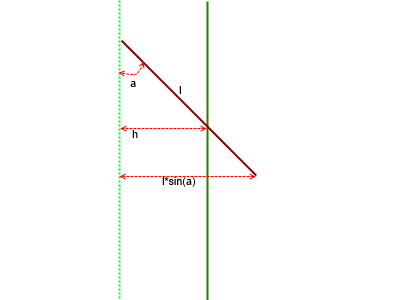
Очевидно, что длина противоположного катета от угла а будет равна синусу угла, умноженного на длину гипотенузы. Тогда мы можем утверждать, что если h меньше либо равна катету напротив угла а, то игла пересекает нить. Изобразим график:
Если мы посчитаем для каждой брошенной иголки h и a и отметим эти точки на предыдущем графике, то картина будет следующая:
Таким образом, вероятность того, что иголка пересечет нить, будет равна отношению площади фигуры под графиком к площади прямоугольника, то есть Пи, умноженное на длину иголки.
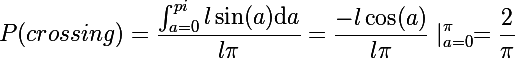
Отсюда и получается искомая аппроксимация числа Пи, что и показал опыт в первой части.
