Собственно речь пойдет о двоичной куче и ее построении с помощью Sift-Down(или Heapify). Многим наверное известно, что построение кучи таким образом осуществляется за 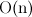 . Здесь я приведу доказательство этого факта.
. Здесь я приведу доказательство этого факта.
Вот пример процедуры построения кучи по массиву на языке Pascal.
Итак, пусть дан массив, состоящий из элементов, и
элементов, и  количество вызовов оператора
количество вызовов оператора 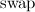 (в процедуре
(в процедуре 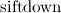 ) при построении кучи по этому массиву. Очевидно,
) при построении кучи по этому массиву. Очевидно,  определяет время работы процедуры
определяет время работы процедуры 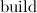 , которое нам и интересно.
, которое нам и интересно.
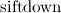 было сделано
было сделано 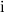 вызовов оператора
вызовов оператора 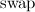 . Тогда его индекс не превосходил
. Тогда его индекс не превосходил 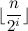 .
.
При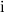 вызовах оператора
вызовах оператора 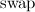 индекс
индекс  элемента возрастает как минимум в
элемента возрастает как минимум в 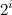 раз. Пусть теперь
раз. Пусть теперь  , т.е.
, т.е.  . Тогда после
. Тогда после 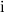 вызовов имеем
вызовов имеем  , что невозможно, так как в нашей куче
, что невозможно, так как в нашей куче  элементов.
элементов. 
Оценим теперь сверху величину . Пусть элемент массива имеет индекс
. Пусть элемент массива имеет индекс  . Найдется
. Найдется 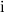 , такое что
, такое что 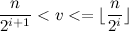 . Тогда для того, чтобы элемент массива с индексом
. Тогда для того, чтобы элемент массива с индексом  встал на свое место в куче потребуется не больше
встал на свое место в куче потребуется не больше 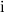 вызовов
вызовов 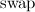 (по лемме). Количество элементов с такими индексами есть величина
(по лемме). Количество элементов с такими индексами есть величина  , которая при
, которая при  обращается в нуль.
обращается в нуль.
Таким образом,

При слагаемые нулевые(поэтому цикл в процедуре
слагаемые нулевые(поэтому цикл в процедуре 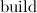 можно начинать с
можно начинать с 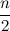 ).
).
Оценим левый множитель в каждом слагаемом суммы, как
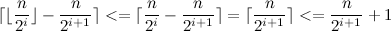
Отсюда имеем:
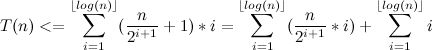
Оценим каждую из сумм.
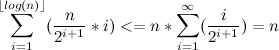
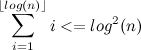
Таким образом,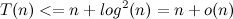 .
.
 ограничена сверху функцией, которая есть
ограничена сверху функцией, которая есть 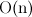 . Значит,
. Значит,  .
.
Следовательно, время работы процедуры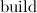 есть величина пропорциональная
есть величина пропорциональная 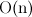 .
.
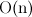 . Здесь я приведу доказательство этого факта.
. Здесь я приведу доказательство этого факта.Вот пример процедуры построения кучи по массиву на языке Pascal.
procedure siftdown(v:longint); var min,l,r:longint; begin l:=v*2; r:=v*2+1; min:=v; if (l <= s) and (a[l] < a[min]) then min:=l; if (r <= s) and (a[r] < a[min]) then min:=r; if min <> v then begin swap(a[min], a[v]); sift_down(min); end; end; procedure build; var i:longint; begin for i:=n downto 1 do siftdown(i); end;
Итак, пусть дан массив, состоящий из
 элементов, и
элементов, и  количество вызовов оператора
количество вызовов оператора 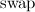 (в процедуре
(в процедуре 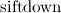 ) при построении кучи по этому массиву. Очевидно,
) при построении кучи по этому массиву. Очевидно,  определяет время работы процедуры
определяет время работы процедуры 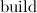 , которое нам и интересно.
, которое нам и интересно.Лемма.
Пусть для какого-то элемента массива при вызове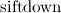 было сделано
было сделано 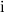 вызовов оператора
вызовов оператора 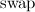 . Тогда его индекс не превосходил
. Тогда его индекс не превосходил 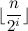 .
. Доказательство:
При
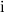 вызовах оператора
вызовах оператора 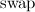 индекс
индекс  элемента возрастает как минимум в
элемента возрастает как минимум в 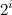 раз. Пусть теперь
раз. Пусть теперь  , т.е.
, т.е.  . Тогда после
. Тогда после 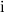 вызовов имеем
вызовов имеем  , что невозможно, так как в нашей куче
, что невозможно, так как в нашей куче  элементов.
элементов. 
Оценим теперь сверху величину
 . Пусть элемент массива имеет индекс
. Пусть элемент массива имеет индекс  . Найдется
. Найдется 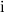 , такое что
, такое что 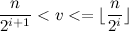 . Тогда для того, чтобы элемент массива с индексом
. Тогда для того, чтобы элемент массива с индексом  встал на свое место в куче потребуется не больше
встал на свое место в куче потребуется не больше 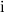 вызовов
вызовов 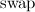 (по лемме). Количество элементов с такими индексами есть величина
(по лемме). Количество элементов с такими индексами есть величина  , которая при
, которая при  обращается в нуль.
обращается в нуль.Таким образом,

При
 слагаемые нулевые(поэтому цикл в процедуре
слагаемые нулевые(поэтому цикл в процедуре 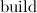 можно начинать с
можно начинать с 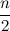 ).
). Оценим левый множитель в каждом слагаемом суммы, как
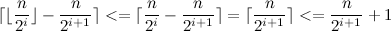
Отсюда имеем:
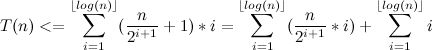
Оценим каждую из сумм.
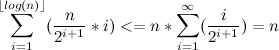
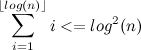
Таким образом,
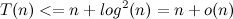 .
. ограничена сверху функцией, которая есть
ограничена сверху функцией, которая есть 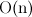 . Значит,
. Значит,  .
.Следовательно, время работы процедуры
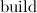 есть величина пропорциональная
есть величина пропорциональная 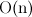 .
.