Пролог: Концепции Boost
Часть 1: Подключение ассоциированных типов без вмешательства в интерфейс исходного класса
Кратко напомню задачу. Есть двумерное игровое поле из клеток, часть из которых свободна, а часть занята. Требуется найти путь по свободным клеткам из одной позиции поля в другую. Алгоритм поиска пути реализован в Boost. Но он требует, чтобы наше поле подходило под определение графа. Точнее класс должен удовлетворять двум концепциям — boost::VertexListGraph и boost:: IncidenceGraph. При этом интерфейс игрового поля менять не хочется — для всего остального проекта это не граф и графом никогда не станет.
В прошлой части было рассмотрено подключение внешних ассоциированных типов, необх��димых для интерпретации класса как boost-графа. Конечно, одних типов недостаточно. Также требуется реализовать несколько функций с заданной сигнатурой и итераторов, с помощью которых библиотека сможет манипулировать игровым полем как графом.
Начнем с функции num_vertices, которая, как можно догадаться из названия, должна возвращать количество вершин графа. Для нашего случая это длинна игрового поля умноженная на ширину. Тип VerticesSizeType определен в первой части статьи (на самом деле это int).
VerticesSizeType num_vertices(const GameField& graph)
{
return graph.getWidth() * graph.getHeight();
}
Теперь можно перейти к реализации первого итератора. Он будет отвечать за перебор всех вершин графа. Ранее мы условились, что вершины будем обозначать целыми числами от нуля до num_vertices. Чтобы избежать написания итератора с нуля, воспользуемся вспомогательным классом boost::forward_iterator_helper. Он позволяет получить полноценный итератор, определив лишь несколько базовых операторов: инкремента (++), сравнения (==) и разыменования (*). Кроме того, алгоритм поиска требует, чтобы для итератора существовал конструктор по умолчанию. Естественно в таком виде использование объекта невозможно — перед применением библиотека присвоит итератору корректное значение.
Для начала посмотрим на интерфейс класса
class VertexIteratorImpl : public boost::forward_iterator_helper<VertexIteratorImpl, Vertex, std::ptrdiff_t, Vertex*, Vertex>
{
public:
VertexIteratorImpl();
VertexIteratorImpl(const GameField& field, int index);
void operator++ ();
bool operator== (const VertexIteratorImpl& anotherIterator) const;
Vertex operator*() const;
private:
bool isValid();
int mIndex;
const GameField* mField;
};
Итератор хранит номер текущей вершины и указатель на игровое поле. Явный конструктор по умолчанию просто должен быть — «рабочего» объекта он не создает:
VertexIteratorImpl::VertexIteratorImpl()
: mField(NULL)
, mIndex(0)
{
}
Второй конструктор позволяет создать полнофункциональный объект
VertexIteratorImpl::VertexIteratorImpl(const GameField& field, int index)
: mField(&field)
, mIndex(index)
{
}
isValid — вспомогательная функция, которая проверяет, находится ли итератор в корректном состоянии (игровое поле задано, индекс имеет допустимое значение)
bool VertexIteratorImpl::isValid()
{
return (mField != NULL) && (mIndex < num_vertices(*mField)) && (mIndex >=0);
}
Учитывая, что вершина — это число, реализация операторов предельно проста, и сводится к работе с полем mIndex. Вот проверка на равенство
bool VertexIteratorImpl::operator== (const VertexIteratorImpl& anotherIterator) const
{
return mIndex == anotherIterator.mIndex;
}
Так осуществляется приращение итератора — нужно только проверить, не превысил ли индекс число вершин графа
void VertexIteratorImpl::operator++ ()
{
if (isValid()) {
++mIndex;
}
}
Разыменование сводится к возврату номера вершины
Vertex VertexIteratorImpl::operator*() const
{
return mIndex;
}
После этого появляется возможность создать еще одну функцию, требуемую концепциями графов — vertices. Возвращать она должна два итератора вершин — начальный и следующий за последним (аналог end() в стандартных коллекциях).
std::pair<VertexIterator, VertexIterator> vertices(const GameField& graph)
{
return std::make_pair(VertexIterator(graph, 0), VertexIterator(graph, num_vertices(graph)));
}
Тип VertexIterator определен в первой части статьи (это псевдоним VertexIteratorImpl). Теперь зададим ребра. Для начала нужно определить пару функций, которые, получив ребро, будут возвращать его начальную и конечную вершину.
Vertex source(Edge edge, const GameField &graph)
{
return edge.first;
}
Vertex target(Edge edge, const GameField &graph)
{
return edge.second;
}
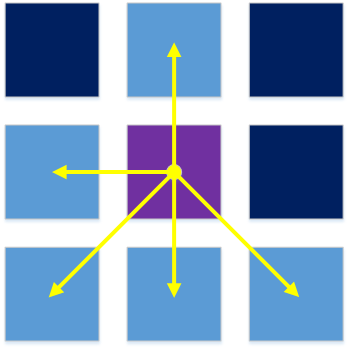
Вторым параметром им должен передаваться граф, даже если для работы он не нужен (в нашем случае ребро — это пара вершин). Остается создать итератор исходящих из заданной вершины ребер. Он немного сложнее в реализации, но все равно достаточно примитивен. Алгоритм работы: проверить 8 вершин вокруг заданной, если они свободны, значит, ребра есть, если заняты, то пути в этом направлении не существует. Начнем с интерфейса
class OutEdgeIteratorImpl : public boost::forward_iterator_helper<OutEdgeIterator, Edge, std::ptrdiff_t, Edge*, Edge>
{
public:
OutEdgeIteratorImpl(const GameField& field, Vertex cellPosition, int index = 0);
OutEdgeIteratorImpl();
Edge operator*() const;
void operator++ ();
bool operator== (const OutEdgeIterator& other) const;
private:
Vertex getCurrentPosition() const;
Vertex getTargetPosition() const;
void updateShift();
bool isValid();
int mShift;
Vertex mCellPosition;
const GameField* mField;
static const int sShiftsX[8];
static const int sShiftsY[8];
};
sShiftsX и sShiftsY — это массивы со смещениями по осям x и y для перебора соседних вершин.
const int OutEdgeIteratorImpl::sShiftsX[8] = {
-1, 0, 1,
-1, 1,
-1, 0, 1 };
const int OutEdgeIteratorImpl::sShiftsY[8] = {
1, 1, 1,
0, 0,
-1, -1, -1};
С конструкторами та же ситуация, которая была для итератора вершин — конструктор по умолчанию создает объект-пустышку (нужен для работы библиотеки), вторым конструктором будем пользоваться сами.
OutEdgeIteratorImpl::OutEdgeIteratorImpl()
: mField(NULL)
, mCellPosition(0)
, mShift(0)
{
}
OutEdgeIteratorImpl::OutEdgeIteratorImpl(const GameField& field, Vertex cellPosition, int index/* = 0*/)
: mField(&field)
, mCellPosition(cellPosition)
, mShift(index)
{
updateShift();
}
В отличие от обхода вершин, здесь не получится возвращать все ребра подряд — часть из них может не существовать. Поэтому оператор приращения будет содержать метод updateShift, задача которого — проверить допустимость текущего положения итератора и при необходимости «прокрутить» его дальше.
void OutEdgeIteratorImpl::operator++ ()
{
++mShift;
updateShift();
}
Проверка осуществляется с помощью метода игрового поля GameField::canPass(int x, int y), если он вернет ложь (в заданную ячейку пути нет), будет проверяться следующая соседняя ячейка. Исходящих ребер может быть от нуля до восьми.
void OutEdgeIteratorImpl::updateShift()
{
if (isValid()) {
int x, y;
std::tie(x, y) = getCoordinates(mCellPosition, *mField);
int dx = sShiftsX[mShift];
int dy = sShiftsY[mShift];
if (!mField->canPass(x + dx, y + dy)) {
++mShift;
updateShift();
}
}
}
bool OutEdgeIteratorImpl::isValid()
{
return (mField != NULL) && (mShift < 8) && (mShift >=0);
}
Также итератор содержит два вспомогательных метода, возвращающих начальную вершину (которая была передана в конструктор) и исходящую (вычисляемую на основе смещения mShift).
Vertex OutEdgeIteratorImpl::getCurrentPosition() const
{
return mCellPosition;
}
Vertex OutEdgeIteratorImpl::getTargetPosition() const
{
return getCurrentPosition() + sShiftsX[mShift] + mField->getWidth() * sShiftsY[mShift];
}
Оператор разыменования возвращает эту пару вершин:
Edge OutEdgeIteratorImpl::operator*() const
{
return std::make_pair(getCurrentPosition(), getTargetPosition());
}
Сравнение итераторов ребер, как и для случая с вершинами, сводится к сравнению числовых индексов
bool OutEdgeIteratorImpl::operator== (const OutEdgeIteratorImpl& other) const
{
return mShift == other.mShift;
}
И остается последний шаг — определить функции перебора ребер, работающие на основе созданных итераторов. Так будет выглядеть функция перебора исходящих ребер для заданной вершины
std::pair<OutEdgeIterator, OutEdgeIterator> out_edges(Vertex v, const GameField& graph)
{
return std::make_pair(OutEdgeIterator(graph, v, 0), OutEdgeIterator(graph, v, 8));
}
В качестве итератора окончания передается объекта с индексом 8, так как ребра с таким номером б��ть не может (допустимые значения от 0 до 7). Функция определения количества исходящих ребер также использует итератор OutEdgeIterator — она сосчитывает ребра перебором
DegreeSizeType out_degree(Vertex v, const GameField& graph)
{
DegreeSizeType result = 0;
std::pair<OutEdgeIterator, OutEdgeIterator> edges = out_edges(v, graph);
for (OutEdgeIterator i = edges.first; i != edges.second; ++i) {
++result;
}
return result;
}
Все. Теперь можно написать функции проверки концепций и насладиться результатом — наше игровое поле одновременно удовлетворяет требованиям к графам двух типов:
boost::function_requires<boost::VertexListGraphConcept<GameField> >();
boost::function_requires<boost::IncidenceGraphConcept<GameField> >();
На этом реализация концепций завершается. Для работы алгоритмов поиска пути потребуется еще несколько доработок — о них я расскажу в заключительной статье цикла.
