
Тетрапептид HABR несравненен
Сравнение последовательностей символов — простое, казалось бы, дело, но, приложенное к биологии, практически на ровном месте встречает кучу проблем. Некоторые задачи современной биологии и вовсе не могут быть решены на современном этапе развития вычислительной техники. В этой статье я на пальцах покажу, что же такого особенного в биологических последовательностях и почему им нужны особые алгоритмы. Биологам и тем более биоинформатикам читать не рекомендуется — есть риск умереть от скуки.
Биологические последовательности — это первичная структура биологических макромолекул. А именно белков и ДНК / РНК. (Есть еще углеводы, например, крахмал, но они состоят из одинаковых мономеров и потому неинтересны.) Последовательность ДНК определяет последовательность белка, последовательность белка определяет его пространственную структуру, структура определяет функции белка, а совокупность функций разных белков называется жизнью. Именно различиями в функционировании разных белков мы, в сущности, и отличаемся друг от друга. Сравнивать молекулы бывает нужно, грубо говоря, по двум причинам:
1) сравнивая попарно белки разных организмов, мы можем сказать, какие организмы более похожи друг на друга, а какие — менее;
2) сравнивая одновременно десяток-другой белков, мы можем найти структурно- и функционально-важные участки (они обычно идентичны у родственных организмов), что бывает полезно при создании искусственных белков (дизайн лекарств, нанотехнологии, в хорошем смысле слова).
Сравнивать лучше именно белки, а не ДНК — хотя бы потому, что у белков «алфавит» больше (20 аминокислот против 4 нуклеотидов), и ниже вероятность случайного совпадения, поэтому дальше речь пойдет именно о белках. Вообще говоря, сравнивать следовало бы структуры, а не последовательности (поскольку мы до сих пор не вполне знаем, как второе определяет первое); но так уж получилось, что выяснять последовательности мы научились хорошо, а получение пространственной структуры — очень трудоемкое дело и вообще, по мнению многих, скорее искусство. Поэтому сравнивать приходится последовательности. Сравнение последовательностей биологических макромолекул называется выравниванием — строки пишутся одна под другой таким образом, чтобы достичь совпадения или сходства символов в наибольшем числе позиций. Одному остатку аминокислоты в белке соответствует одна буква латинского алфавита в последовательности.

Учет степени сходства мономеров
Мы привыкли считать две последовательности тем более похожими, чем больше символов в них совпадает. В биологии такой подход никуда не годится. Рассмотрим две пары последовательностей:
Пара 1 Пара 2ASDLV ASDLVATEIV AWDKVСтарина Хэмминг однозначно говорит, что второе выравнивание лучше: в первой паре совпадают только два символа из пяти, а во второй — три. Но давайте посмотрим на их структуры:
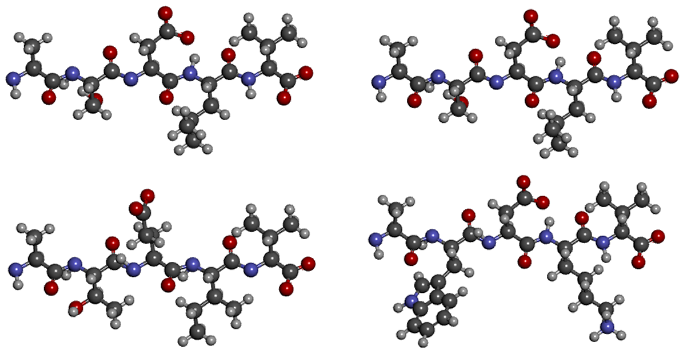
S и T, D и E — те остатки, которыми различаются последовательности первой пары — различаются по структуре ровно на один атом углерода, L и I — вообще изомеры. В большинстве случаев на структуре белка такое различие не отражается. А вот замена маленького полярного серина на большой неполярный триптофан или гидрофобного лейцина на заряженный лизин, как во второй паре, очень сильно изменит структуру молекулы. Таким образом, в первом выравнивании последовательности практически идентичны, а во втором — сильно непохожи.

Учет структурных особенностей сравниваемых символов делается довольно просто: используются т.н. матрицы замен, как та, что на рисунке. Чем большее число на пересечении совпавших букв — тем больше количественный показатель сходства (называемый «Счет», или «Score»).
A S D L V A S D L V A T E I V A W D K VScore = 4+1+2+2+4 = 13 Score = 4-3+6-2+4 = 9 Матрицы составляются на основе статистики замен аминокислот в белках с уже известной структурой: чем чаще наблюдается замена одной буквы на другую, тем и больше число на их пересечении. Проблема же в том, что периодически появляются новые матрицы, лучше прежних; соответственно, все они чем-то плохи и чего-то не учитывают.
Учет вставок и делеций
Не знаю, как других, но меня в свое время поразило, насколько же похожи белки разных организмов. Где человек — а где кролик, а сывороточные альбумины у того и другого различаются всего на несколько аминокислот. Но на несколько всё-таки различаются: мутационная изменчивость — неотъемлемое свойство живого. По сути, оценивая сходство белков, мы оцениваем количество произошедших мутаций на пути эволюционного превращения одного белка в другой. Учет мутаций первого типа — замен — мы рассмотрели выше. Еще два типа — вставки и делеции (удаления) — рассмотрим сейчас.
Вставки и делеции в биоинформатике рассматривают как одну сущность по простой причине — имея две последовательности, в одной из которых есть лишняя буква, мы не можем определить, какая из последовательностей «оригинальная». Гипотетический общий предок обоих организмов вымер миллионы лет назад, поэтому мы точно не знаем, имеет ли место в данном случае вставка или делеция. По этой причине появился термин «индел» (инсерция + делеция); в русской биоинформатике более распространен термин «делеция» или калька с английского «гэп».

Два возможных варианта происхождения родственных последовательностей. Пара последовательностей из нижней строчки — реально существующие «молекулы», вверху — гипотетический предок, который мог быть как слева или как справа (или вообще ни так ни так).
Если в выравнивании есть делеции, они штрафуются. Чем больше делеций — тем больше очков отнимается от счета. И снова рассмотрим два выравнивания:
ASGHDLV AMSDCLVAT--EIV A-TD-VVВ обоих выравниваниях «выпали» по две аминокислоты. В обоих случаях, формально, произошли две мутации. На самом же деле — в первом случае произошла одна мутация. Длиной в два остатка. Но одна. Одно эволюционное событие. И вероятность его больше, чем двух отдельных, как во втором примере. Поэтому счет выравнивания слева должен быть выше, а первые две последовательности должны считаться более похожими.
Для учета делеций используется т.н. аффинный штраф, состоящий из штрафа «за открытие» и «за продолжение» делеции. Первый обычно на порядок-два больше второго (примерно 10 и 1, соответственно, или 10 и 0,1). В примере слева у нас одно открытие и одно продолжение, справа — два открытия.
Проблема учета делеций этим не исчерпывается. В зависимости от места делеции в молекуле она может в большей или меньшей степени влиять на структуру. Некоторые алгоритмы, например, Clustal, учитывают «остаткоспецифичные штрафы», некоторые — нет. Обычно это сводится к тому, что делеции в гидрофильных регионах — потенциальных петлях, болтающихся в водном окружении — штрафуются меньше, чем в гидрофобных (потенциальных плотно упакованных ядрах глобулы). Вопрос, насколько должны различаться эти штрафы, и только ли гидропатичность должна служить критерием различий, по-видимому, каждый решает для себя сам…

Мутация в участке № 1 — плотно упакованном и строго структурированном (бета-тяж) ядре глобулы — может сильно нарушить структуру белка. Мутация в участке № 2 (неструктурированная относительно лабильная петля), скорее всего, никак не повлияет на нее.
Расчет выравнивания
До сих пор мы рассматривали оценку готового выравнивания, не задаваясь вопросом, как оно получается. Среднестатистический белок состоит из нескольких сотен аминокислот, выровнять такие длинные строки «на глазок» явно не получится. Хотя есть разные способы получения выравниваний, оптимальным в настоящее время считается алгоритм Нидлмана — Вунша и его модификации. Суть алгоритма я опущу: математическая аудитория легко разберется в ней самостоятельно, остальным
В начале я говорил, что выравнивая одновременно десяток-другой белков, мы можем найти структурно- и функционально-важные участки в них. Например, аминокислоты на рисунке, составляющие активный центр трипсиноподобных протеаз, четко выдают себя тем, что являются идентичными у 20 подобных белков (соответствующие позиции обозначены звездочками).
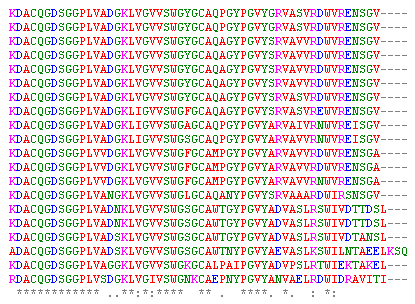
Аминокислоты, определяющие каталитические свойства фермента, являются консервативными, т.е. не меняются в процессе эволюции. Активный центр фермента должен соответствовать геометрии и химии субстрата с точностью до атома, поэтому мутация в нем означает «конец карьеры» фермента как катализатора. На самом деле, конечно, мутации происходят в любом месте молекулы; но белки с мутацией в функциональном участке делают нежизнеспособным своего хозяина, поэтому нам кажется, что их нет.
В условиях, когда получение полной трехмерной структуры белка все еще является в определенном смысле роскошью, возможность находить такие закономерности очень ценна. Засада же здесь в том, что получить математически оптимальное выравнивание даже десятка белков мы не можем. Если для выравнивания двух белков используется двумерный массив, для выравнивания 10 белков нужен, соответственно, десятимерный. Даже если каждая последовательность имеет длину в 100 символов (что соответствует очень маленькому белку), размерность массива получается столь огромной (10010), что современный компьютер будет рассчитывать его тысячи лет. О том, как же все-таки биологи выкручиваются в этой ситуации — расскажу, наверное, уже в другой раз.