 Data Matrix является двумерным матричным штрих кодом, состоящим из светлых и темных участков. С помощью такого штрих кода можно закодировать достаточно большой объем информации (2-3Кб). Часто Data Matrix применяется при маркировке небольших предметов, например микросхем, а также в пищевой, оборонной промышленности, рекламе и других сферах.
Data Matrix является двумерным матричным штрих кодом, состоящим из светлых и темных участков. С помощью такого штрих кода можно закодировать достаточно большой объем информации (2-3Кб). Часто Data Matrix применяется при маркировке небольших предметов, например микросхем, а также в пищевой, оборонной промышленности, рекламе и других сферах.Существует множество сайтов для создания таких кодов, но мне всегда было интересно, каким же образом текст превращается в набор черных и белых квадратиков? Должен же быть какой-то алгоритм?
При создании Data Matrix нам понадобится обратиться к арифметике полей Галуа и кодам Рида-Соломона. Рассмотрим этот процесс на простом примере.
Прежде всего, посмотрим на структуру матрицы:
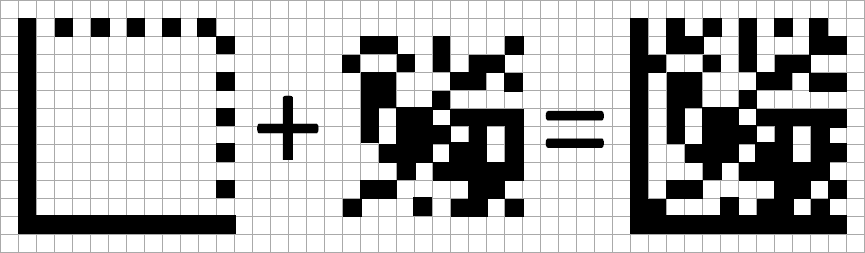
Состоит наша матрица из двух частей: шаблона поиска и закодированных данных. Разумеется, размер матрицы прямо пропорционален размеру входных данных. Вокруг нашего кода обязательно должна быть свободная зона, отделяющая код от остального изображения.
Возьмем какое-нибудь короткое слово, например, “Habr” (без кавычек) и создадим для него Data Matrix. Процесс состоит из двух этапов: на этапе высокоуровневого кодирования нужно получить последовательность кодов данных и кодов коррекции ошибок, а на этапе низкоуровневого кодирования – изобразить в матрице двоичное представление этих кодов.
Высокоуровневое кодирование
В Data Matrix, как и в QR-коде, используются коды Рида-Соломона над полем Галуа
 (число 8 выбрано, поскольку каждое кодовое слово занимает в матрице 8 бит). Существует несколько неприводимых многочленов, позволяющих сгенерировать такое поле. Среди них
(число 8 выбрано, поскольку каждое кодовое слово занимает в матрице 8 бит). Существует несколько неприводимых многочленов, позволяющих сгенерировать такое поле. Среди них 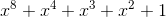 (в десятичном представлении 285, используется для QR-кодов) и
(в десятичном представлении 285, используется для QR-кодов) и 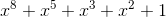 (301, используется в Data Matrix).
(301, используется в Data Matrix).Для расчетов нам понадобится таблица степеней двойки для каждого элемента поля. Создается эта таблица довольно просто: если показатель степени
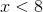 , то возведение в сте��ень выполняется как обычно. В противном случае
, то возведение в сте��ень выполняется как обычно. В противном случае  , после чего производится побитовое сложение по модулю 2 с десятичным представлением взятого неприводимого многочлена, если
, после чего производится побитовое сложение по модулю 2 с десятичным представлением взятого неприводимого многочлена, если  . Например,
. Например,  ,
, 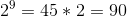 и т. д.
и т. д.Необходимо получить кодовое слово
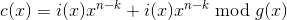 ,
,где
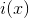 – информационный многочлен,
– информационный многочлен,  – порождающий многочлен,
– порождающий многочлен, 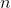 – общая длина кода вместе с корректировочными,
– общая длина кода вместе с корректировочными, 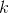 – количество информационных кодов (вместе с кодами отступа, о них – далее),
– количество информационных кодов (вместе с кодами отступа, о них – далее),  – операция взятия остатка от деления.
– операция взятия остатка от деления.Создадим для начала информационный многочлен. Для этого нам понадобится знать, какого размера должна быть матрица, чтобы можно было разместить все информационные коды:

Из таблицы видно, что для кодирования строки из 4х элементов нужно взять матрицу размером 12x12 («полезная» область – 10x10), в которую помещаются 5 кодов данных и 7 кодов коррекции.
Для символов таблицы ASCII код получается следующим образом: C=ASCII value+1. Например, для символа ‘H’ C=72+1=73.
Подряд идущие цифры объединяются в пары, и для них C=N+130, где N – число, полученное в результате группировки. Например, если рядом стоят цифры 2 и 5, то C=25+130=155.
Поскольку элементов у нас меньше, чем должно быть (вместо пяти только четыре), необходимо добавить специальные коды отступа. Первым таким кодом всегда является 129. Последующие коды отступа, до первого кода коррекции ошибок, вычисляются так:
 , где
, где 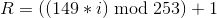 – псевдослучайное число,
– псевдослучайное число,  – номер элемента.
– номер элемента.Для слова “Habr” получаем следующую последовательность кодов: 73, 98, 99, 115, 129.
Теперь мы можем записать информационный многочлен:
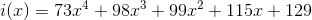
и домножить его на
 (
( – число кодов коррекции):
– число кодов коррекции): 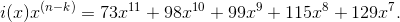
Перейдем к созданию порождающего многочлена. Вычисляется он по следующей формуле:
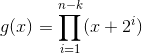
Начинаем перемножать скобки:
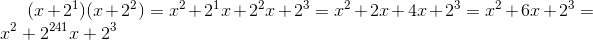

Сложение в нашем поле определено как побитовое сложение по модулю 2. Сначала выполняется возведение в степень с помощью таблицы, затем их сложение и нахождение «логарифма» полученного числа для возврата к степеням двойки. В случае если после сложения степеней пол��чается число, большее 254, берем его остаток от деления на
 .
.После перемножения всех скобок и возведения в степень получим:

Последняя операция, завершающая высокоуровневое кодирование, и, пожалуй, самая сложная – нахождение остатка от деления
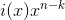 на
на  :
: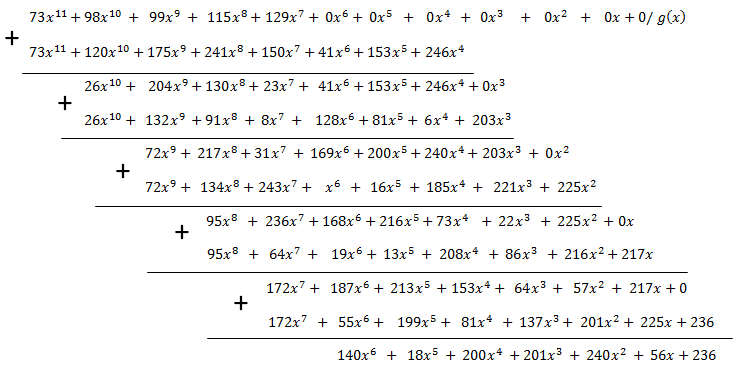
Выполняется деление многочленов в столбик, но с учетом того, что вычитание, определенное точно так же, как и сложение, и умножение выполняются в поле Галуа.
Теперь мы можем записать кодовое слово
 полностью:
полностью:
Низкоуровневое кодирование
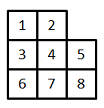 Каждый из полученных выше кодов представляется в Data Matrix в виде квадрата размером 3х3 ячейки без правого верхнего уголка. 1 здесь соответствует старшему биту, 8 – младшему. Нужно заполнить такими элементами всю матрицу.
Каждый из полученных выше кодов представляется в Data Matrix в виде квадрата размером 3х3 ячейки без правого верхнего уголка. 1 здесь соответствует старшему биту, 8 – младшему. Нужно заполнить такими элементами всю матрицу. Приготовим сетку 10х10 (именно такого размера должна быть матрица в данном случае), на которой нарисуем контуры первых пяти элементов, как на рисунке справа. Вне зависимости от того, какого размера матрица, эти элементы всегда располагаются именно так, и никак иначе.
Приготовим сетку 10х10 (именно такого размера должна быть матрица в данном случае), на которой нарисуем контуры первых пяти элементов, как на рисунке справа. Вне зависимости от того, какого размера матрица, эти элементы всегда располагаются именно так, и никак иначе.Остальные элементы размещаются аналогичным образом, но прежде чем нарисовать их, необходимо отметить несколько особых случаев, связанных с углами матрицы.
Если
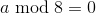 , где a – сторона квадрата, то перед нами самый простой случай, когда после размещения всех элементов непоместившиеся участки просто переносятся на противоположную сторону.
, где a – сторона квадрата, то перед нами самый простой случай, когда после размещения всех элементов непоместившиеся участки просто переносятся на противоположную сторону.Если
 , то в правом нижнем углу остается «лишний» квадратик размером 2х2, который заполняется так:
, то в правом нижнем углу остается «лишний» квадратик размером 2х2, который заполняется так:
Если
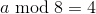 или
или  , то следует обратить внимание на левый нижний и правый верхний угол, особенно на нумерацию битов:
, то следует обратить внимание на левый нижний и правый верхний угол, особенно на нумерацию битов:
Есть еще два случая, которые возникают только при построении прямоугольных матриц, поэтому мы их опустим.
Вернемся к нашей матрице и добавим все остальные элементы, а также укажем, какому кодовому слову соответствует каждый элемент. Стрелками показано, каким образом производится нумерация:

После переноса непоместившихся элементов получаем:

В правом нижнем углу остался незанятый квадрат (
 , что как раз соответствует такому случаю). Занесем в таблицу все наши коды в таком же порядке, в каком они идут в
, что как раз соответствует такому случаю). Занесем в таблицу все наши коды в таком же порядке, в каком они идут в  , и их двоичные представления:
, и их двоичные представления:
Аккуратно заполняем матрицу. Начнем с шаблона поиска и нижнего квадрата, а затем по очереди добавляем каждый код:
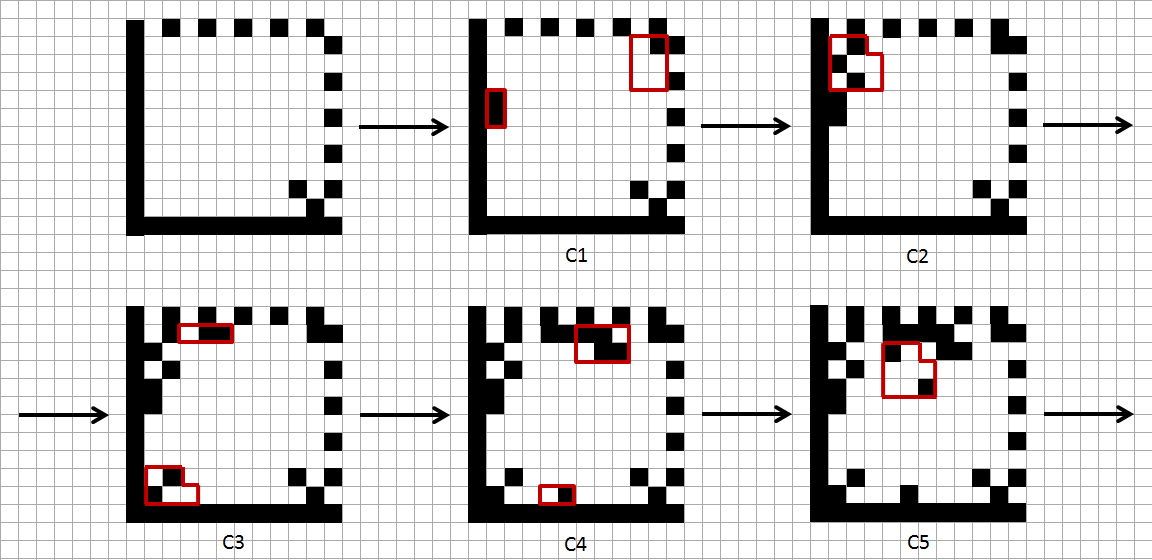
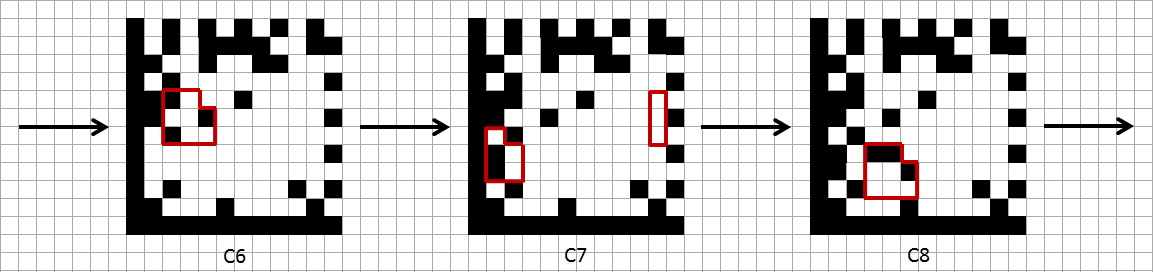
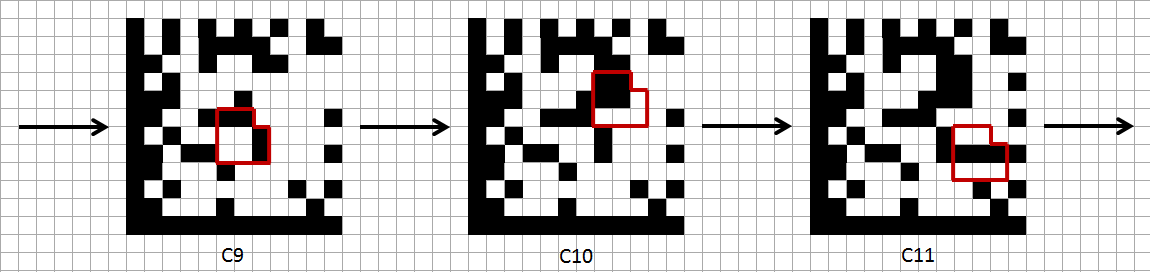
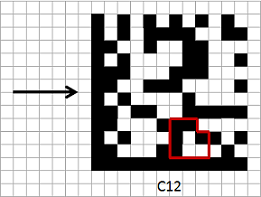
Итак, наш код Data Matrix готов:

