В предыдущей статье мы на основе общих друзей ВКонтакте строили граф, а сегодня поговорим о том, как получить список друзей, друзей друзей и так далее. Предполагается, что вы уже прочли предыдущую статью, и я не буду описывать все заново. Под хабракатом большие картинки и много текста.
Начнем с того, что просто скачать все id пользователей достаточно легко, список валидных id можно найти в Каталоге пользователей Вконтакте. Наша же задача — получить список друзей выбранного нами id пользователя, их друзей и рекурсивно сколь угодно глубоко, в зависимости от указанной глубины.
Код, опубликованный в статье, будет меняться с течением времени, поэтому более свежую версию можно найти в том же проекте на Github.
Как будем реализовывать:
Что будем использовать:
Что нам потребуется в начале — это указать глубину (deep), с которой мы хотим работать. Сделать это можно сразу в settings.py:
deep равное 1 — это наши друзья, 2 — это друзья наших друзей и так далее. В итоге мы получим словарь, ключами которого будут id пользователей, а значениями — их список друзей.
Не спешите выставлять большие значения глубины. При 14 моих исходных друзьях и глубине равной 2, количество ключей в словаре составило 2427, а при глубине, равной 3, у меня не хватило терпения дождаться завершения работы скрипта, на тот момент словарь насчитывал 223 908 ключей. По этой причине мы не будем визуализировать такой огромный граф, ведь вершинами будут ключи, а ребрами — значения.
Добиться нужного нам результата поможет уже известный метод friends.get, который будет расположен в хранимой процедуре, имеющей следующий вид:
Напоминаю, что хранимую процедуру можно создать в настройках приложения, пишется она на VkScript, как и execute, документацию можно прочесть здесь и здесь.
Теперь о том, как она работает. Мы принимаем строку из 25 id, разделенных запятыми, вынимаем по одному id, делаем запрос к friends.get, а нужная нам информация будет приходить в словаре, где ключи — это id, а значения — список друзей данного id.
При первом запуске мы отправим хранимой процедуре список друзей текущего пользователя, id которого указан в настройках. Список будет разбит на несколько частей (N/25 — это и число запросов), связано это с ограничением количества обращений к API ВКонтакте.
Всю полученную информацию мы сохраняем в словаре, например:
Ключи 1, 2 и 3 были получены при глубине, равной 1. Предположим, что это и были все друзья указанного пользователя (0).
Если глубина больше 1, то далее воспользуемся разностью множеств, первое из которых — значения словаря, а второе — его ключи. Таким образом, мы получим те id (в данном случае 0 и 4), которых нет в ключах, разобьем их опять на 25 частей и отправим хранимой процедуре.
Тогда в нашем словаре появятся 2 новых ключа:
Сам же метод deep_friends() выглядит следующим образом:
Конечно, это быстрее, чем кидать по одному id в friends.get без использования хранимой процедуры, но времени все равно занимает порядочно много.
Если бы friends.get был похож на users.get, а именно мог принимать в качестве параметра user_ids, то есть перечисленные через запятую id, для которых нужно вернуть список друзей, а не по одному id, то код был бы намного проще, да и количество запросов было в разы меньше.
Возвращаясь к началу статьи, могу снова повторить — очень медленно. Хранимые процедуры не спасают, решение alxpy с многопоточностью (спасибо ему за вклад и участиехоть кому-то было интересно, кроме меня) ускоряло на несколько секунд работу программы, но хотелось большего.
Мудрый совет получил от igrishaev — нужен какой-то мап-редьюс.
Дело в том, что ВКонтакте разрешает 25 запросов к API через execute, из этого следует, что если делать запросы с разных клиентов, то мы можем увеличить количество допустимых запросов. 5 тачек — это уже 125 запросов �� секунду. Но и это далеко не так. Забегая вперед, скажу, что можно и еще быстрее, примерно будет выглядеть следующим образом (на каждой машине):
Если нам приходит сообщение об ошибке, то мы делаем запрос снова, спустя заданное количество секунд. Такой прием работает какое-то время, но затем ВКонтакте начинает присылать во всех ответах None, поэтому после каждого запроса честно будем ждать 1 секунду. Пока что.
Далее нам надо выбрать новые инструменты или же написать свои, чтобы реализовать задуманное. В итоге у нас должна получиться горизонтально масштабируемая система, принцип работы видится мне следующим образом:
А если вы видели эту картинку, то понимаете, на какой брокер сообщений я намекаю.
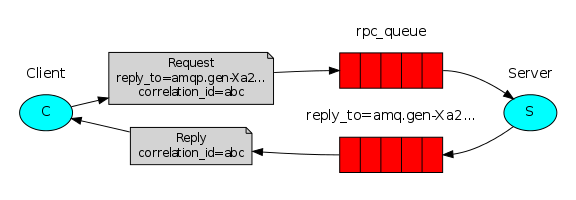
Как только все ответы приняты, объединяем их в один. Далее результат можно будет вывести на экран или вовсе сохранить, об этом позже.
Тут стоит заметить, что код изменится, и если вам было достаточно использовать предыдущую версию проекта, то она так и осталась в неизменном виде. Весь код, который будет ниже, относится к новому релизу.
В качестве брокера сообщений будем использовать RabbitMQ, асинхронной распределенной очереди заданий — Celery.
Для тех, кто никогда с ними не сталкивался, вот несколько полезных ссылок на материалы, которые советую вам прочитать:
Не надо бояться понять, хоть и говорят, что можно конкретно повернуть свою голову, когда начинаешь «думать не одним компьютером, а несколькими», но это вовсе не так.
Если у вас Mac, как и у автора, то RabbitMQ шикарно ставится через Homebrew:
Celery же ставится еще легче, используем третью ветку Python:
У меня Celery установлен на Linux Mint, а RabbitMQ — на Mac. С виндой, как обычно, проблемы —тяжело найти, легко потерять она почему-то все время не хотела возвращать response моему Mac.
Далее создадим virtual host, пользователя и дадим ему права:
В конфигурации RabbitMQ надо указать ip хоста, на котором он установлен:
Вот несколько возможных конфигураций, какую выбрать — решать вам.
Если у вас роутер или еще что-то, полезно будет знать, что RabbitMQ использует 5672 порт, ну и сделать переадресацию в настройках вашего устройства. Скорее всего, если будете тестировать, то воркеров раскидаете по разным машинам, а им нужно будет использовать брокер, и, если не правильно настроите сеть, Celery до RabbitMQ так и не достучится.
Очень хорошей новостью является то, что ВКонтакте разрешает делать по 3 запроса в секунду с одного id. Умножим эти запросы на количество возможных обращений к API ВКонтакте (25), получим максимальное число обрабатываемых контактов в секунду (75).

Если у нас будет много воркеров, то настанет момент, когда начнем переходить за дозволенный лимит. Поэтому переменная token (в settings.py) теперь будет кортежем, содержащим в себе несколько токенов с разных id. Скрипт же будет при каждом запросе к ВКонтакте API выбирать один из них рандомным образом:
В этом плане у вас не должно возникнуть сложностей, если есть несколько аккаунтов в ВКонтакте (можно напрячь друзей, родных), у меня не было проблем с 4 токенами и 3 воркерами.
Нет, вам никто не мешает использовать time.sleep(), или пример выше с while, но тогда готовьтесь получать сообщения об ошибках (возможны вообще пустые ответы — id:None), или подольше ждать.
Самое интересное из файла call.py:
Как видите, в 2 функциях мы используем groups(), который параллельно запускает несколько заданий, после чего мы «склеиваем» ответ. Помните, как deep_friends() выглядел вначале (там уж очень старый при��ер — даже без многопоточности)? Смысл остался тем же — мы используем разность множеств.
И, наконец, tasks.py. Когда-нибудь эти замечательные функции объединятся в одну:
Когда все настроено, запускаем RabbitMQ командой:
Затем переходим в папку проекта и активируем воркера:
Теперь, чтобы получить и сохранить список общих или «глубинных» друзей, достаточно скомандовать в консоли:
Напомню, что у автора статьи, которая вдохновила меня на первую часть, 343 друга (запрос на общих друзей) «обрабатывались» за 119 секунд.
Мой вариант из предыдущей статьи делал то же самое за 9 секунд.
Сейчас у того автора другое число друзей — 308. Что же, придется сделать один лишний запрос для последних восьми id, потратить на него драгоценную секунду, хотя за ту же секунду можно обработать 75 id.
С одним воркером работа скрипта заняла 4.2 секунды, с двумя воркерами — 2.2 секунды.
Если 119 округлим до 120, а 2.2 до 2, то мой вариант работает в 60 раз быстрее.
Что касается «глубинных друзей» (друзья моих друзей и так далее + тестируем на другом id, чтобы ждать меньше) — при глубине, равной 2, количество ключей в словаре составило 1 251.
Время выполнение кода, приведенного в самом начале статьи, — 17.9 секунды.
Одним воркером время выполнения скрипта — 15.1 секунды, с двумя воркерами — 8.2 секунды.
Таким образом, deep_friends() стал быстрее примерно в 2.18 раза.
Да, не всегда результат такой радужный, иногда ответа на один запрос в ВКонтакте приходится ждать и по 10, и по 20 секунд (хотя частое время выполнения одного задания 1.2 — 1.6 секунд), скорее всего, это связано с нагрузкой на сервис, ведь мы не одни во вселенной.

В итоге, чем больше воркеров сделать, тем быстрее будет обрабатываться результат. Не забудьте про мощность своего железа, дополнительные токены, сеть (например, у автора резко возрастало время выполнения скрипта, когда он юзал свой айфон в качестве точки доступа) и иные факторы.
Да, есть много графо-ориентированных БД. Если в дальнейшем (а оно так и будет), мы захотим анализировать полученные результаты, то все равно их надо будет где-то хранить до самого анализа, потом эти же результаты выгружать в память и производить с ними какие-нибудь действия. Не вижу смысла использовать какую-нибудь субд, если проект был бы коммерческим и нас интересовало, например, что происходит с графом конкретного пользователя на протяжении времени — то да, тут обязательна графо-ориентированная бд, но, поскольку заниматься анализом будем в «домашних условиях», pickle нам хватит вполне.
Перед сохранением словарей логично будет удалять из них ключи, значения которых None. Это заблокированные или удаленные аккаунты. Проще говоря, эти id будут присутствовать в графе, потому что они есть у кого-то в друзьях, ну а мы сэкономим на количестве ключей в словаре:
Как видно, если мы где-то сохранили результат, то где-то и должны его загрузить, дабы заново не собирать id.
Чтобы не писать свой велосипед, воспользуемся довольно известным networkx, который сделает за нас всюгрязную работу. Больше узнать про networkx вы можете из этой статьи.
Прежде чем начнем анализировать граф, нарисуем его. networkx для этого понадобится matplotlib:
Далее нам надо создать сам граф. Вообще, есть 2 пути.
Первый сожрет много оперативной памяти и вашего времени:
И это не автор выжил из ума, нет. Подобный пример приводится на странице университета Райса (Rice University), под заголовком Convert Dictionary Graph Representation into networkx Graph Representation:
Можете поверить мне на слово, граф строился целый вечер, когда в нем было уже более 300 000 вершин, мое терпение лопнуло.Если вы прошли курс на Сoursera по Python от этого университета, то понимаете, о чем я. А я всем на курсе говорил, что не так людей учат, ну да ладно.
Да, приводится пример для ориентированного графа, но суть остается той же — сначала добавляем ключи, делая их вершинами, потом делаем вершинами значения, и то если их еще нет в графе, а потом соединяем их ребрами (в моем варианте).
А второй способ сделает все за секунды:
Код лежит в файле graph.py, чтобы нарисовать граф общих друзей достаточно запустить этот скрипт или же где-нибудь создать экземпляр класса VkGraph(), а затем вызвать его метод draw_graph().
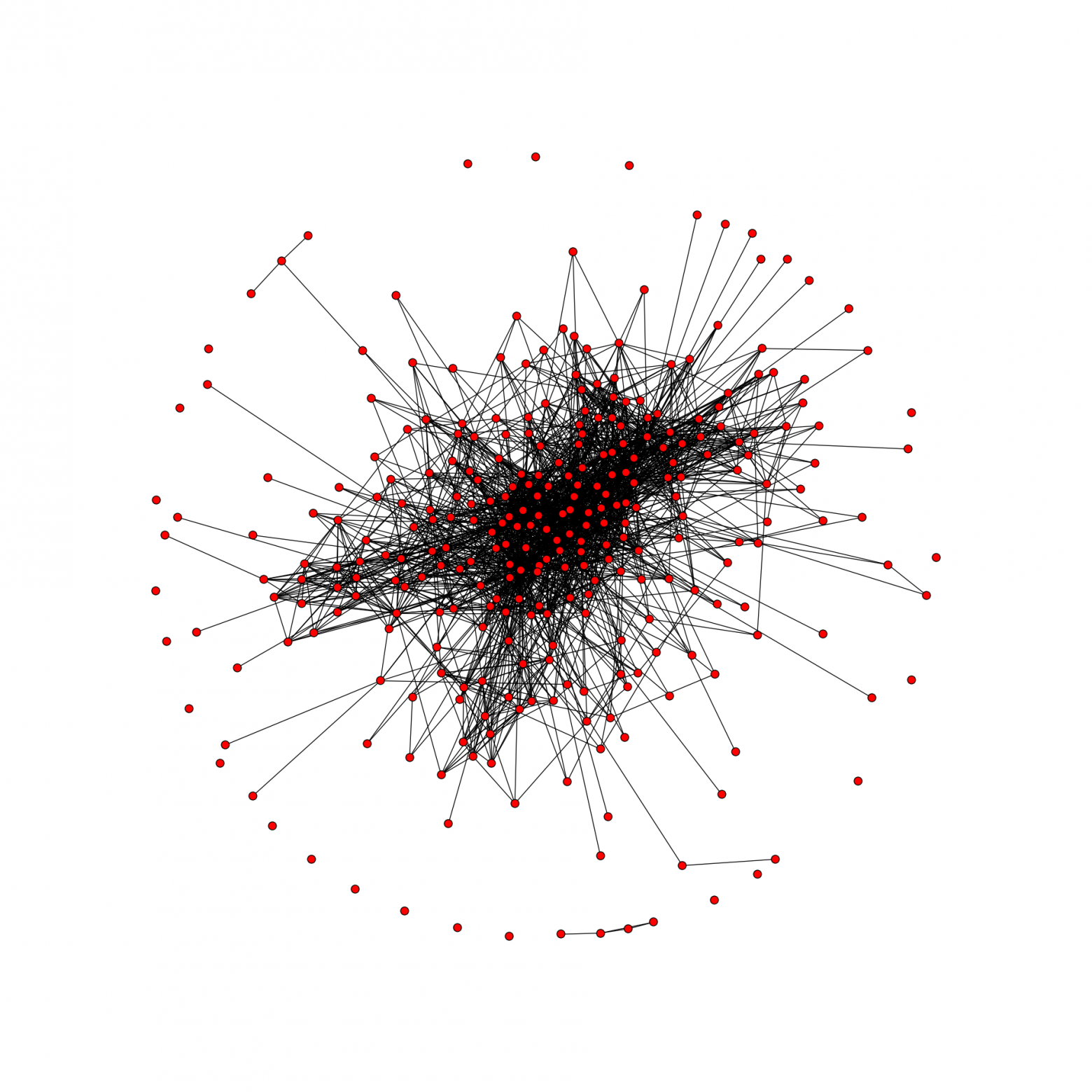
Это граф общих друзей, всего 306 вершин и 2096 ребер. К сожалению, я ни разу не дизайнер (практически все настройки стандартные), но вы всегда сможете стилизовать граф «под себя». Вот пара ссылок:
А сам метод выглядит так:
В итоге вы получаете картинку date graph.png в папке проекта. Не советую рисовать граф для глубинных друзей. При 308 друзьях и глубиной равной 2, в словаре оказалось более 145 000 ключей. А есть ведь еще и значения — кортежи с id, которых вряд ли будет мало.
Долго искал самый малосодержащий друзей профиль в ВКонтакте, хотя тут важнее — друзья-друзей. 10 начальных друзей (1 из них заблокированный и автоматически удалится), при нашей стандартной глубине (2), в словаре насчитывалось 1234 ключа и 517 174 id (из значений). Примерно 419 друзей у одного id. Да, там есть и общие друзья, когда построим граф, мы это поймем:
Вернет:
С такими большими данными было бы неплохо поиграться. У networkx очень большой список алгоритмов, которые можно применять к графам. Разберем некоторые из них.
Для начала определим, связный ли у нас граф:
Связный граф — это такой граф, в котором любая пара вершин соединена маршрутом.
Кстати, у того же самого id при глубине, равной 1, вот такой красивый граф, содержащий 1268 вершин и 1329 ребер:

Вопрос знатокам. Раз у нас получается граф друзья-друзей, он по-любому должен быть связным. Не может быть такого, чтобы из ниоткуда появлялась вершина, которая не связана ни с одной из существующих. Однако мы видим справа одну вершину, которая не соединена ни с одной. Почему? Призываю сначала подумать, интереснее будет узнать истину.
Будем считать, что у вас не будет такой ситуации, то есть скорее всего вы увидите True.
Вспомним, что диаметром графа называется максимальное расстояние между двумя его вершинами.
Центр графа — это любая вершина, такая, что расстояние от нее до наиболее отдаленной вершины минимально. Центром графа может быть одна вершина или несколько вершин. Или проще. Центр графа — вершина, эксцентриситет (расстояние от этой вершины до самой удаленной от нее) которой равен радиусу.
Вернет список вершин, которые являются центром графа. Не удивляйтесь, если центром окажется id, указанный в settings.py.
Радиус графа — это наименьший из эксцентриситетов всех вершин.
Этот тот самый Page Rank, о котором вы подумали. Как правило, алгоритм используется для веб-страничек или иных документов, связанных ссылками. Чем больше ссылок на страницу, тем она важнее. Но никто не запрещает использовать этот алгоритм для графов. Более точное и подходящее определение позаимствуем из этой статьи:
Цитируя Википедию:
Как видите, нет ничего сложного, и networkx предлагает еще много алгоритмов (автор насчитал 148), которые можно применять к графам. Вам остается лишь выбрать нужный вам алгоритм и вызвать соответствующий метод в файле graph.py.
Мы сделали распределенную систему, позволяющую собирать и строить граф общих друзей в ВКонтакте, которая работает в 60 раз быстрее (в зависимости от количества воркеров), чем предложенный вариант от Himura, также реализовали новую функцию — запрос всех «глубинных друзей», добавили возможность анализа построенных графов.
Если вы не хотите ставить дополнительное ПО и вам надо построить красивый граф общих друзей из предыдущей статьи, то старый релиз к вашим услугам. В нем вы также найдете старую версию получения списка друзей пользователя рекурсивно сколь угодно глубоко.
Это вовсе не предел, будут продолжаться работы по увеличению быстродействия программы.
По-прежнему жду от вас вкусных пулл-реквестов, особенно если вы занимаетесь визуализированием данных. Спасибо за внимание!
Начнем с того, что просто скачать все id пользователей достаточно легко, список валидных id можно найти в Каталоге пользователей Вконтакте. Наша же задача — получить список друзей выбранного нами id пользователя, их друзей и рекурсивно сколь угодно глубоко, в зависимости от указанной глубины.
Код, опубликованный в статье, будет меняться с течением времени, поэтому более свежую версию можно найти в том же проекте на Github.
Как будем реализовывать:
- Задаем нужную нам глубину
- Отправляем исходные данные либо те id, которые надо исследовать на данной глубине
- Получаем ответ
Что будем использовать:
- Python 3.4
- Хранимые процедуры в ВКонтакте
Задаем нужную нам глубину
Что нам потребуется в начале — это указать глубину (deep), с которой мы хотим работать. Сделать это можно сразу в settings.py:
deep = 2 # такая строчка там уже есть
deep равное 1 — это наши друзья, 2 — это друзья наших друзей и так далее. В итоге мы получим словарь, ключами которого будут id пользователей, а значениями — их список друзей.
Не спешите выставлять большие значения глубины. При 14 моих исходных друзьях и глубине равной 2, количество ключей в словаре составило 2427, а при глубине, равной 3, у меня не хватило терпения дождаться завершения работы скрипта, на тот момент словарь насчитывал 223 908 ключей. По этой причине мы не будем визуализировать такой огромный граф, ведь вершинами будут ключи, а ребрами — значения.
Отправление данных
Добиться нужного нам результата поможет уже известный метод friends.get, который будет расположен в хранимой процедуре, имеющей следующий вид:
var targets = Args.targets; var all_friends = {}; var req; var parametr = ""; var start = 0; // из строки с целями вынимаем каждую цель while(start<=targets.length){ if (targets.substr(start, 1) != "," && start != targets.length){ parametr = parametr + targets.substr(start, 1); } else { // сразу делаем запросы, как только вытащили id req = API.friends.get({"user_id":parametr}); if (req) { all_friends = all_friends + [req]; } else { all_friends = all_friends + [0]; } parametr = ""; } start = start + 1; } return all_friends;
Напоминаю, что хранимую процедуру можно создать в настройках приложения, пишется она на VkScript, как и execute, документацию можно прочесть здесь и здесь.
Теперь о том, как она работает. Мы принимаем строку из 25 id, разделенных запятыми, вынимаем по одному id, делаем запрос к friends.get, а нужная нам информация будет приходить в словаре, где ключи — это id, а значения — список друзей данного id.
При первом запуске мы отправим хранимой процедуре список друзей текущего пользователя, id которого указан в настройках. Список будет разбит на несколько частей (N/25 — это и число запросов), связано это с ограничением количества обращений к API ВКонтакте.
Получение ответа
Всю полученную информацию мы сохраняем в словаре, например:
{1:(0, 2, 3, 4), 2: (0, 1, 3, 4), 3: (0, 1, 2)}
Ключи 1, 2 и 3 были получены при глубине, равной 1. Предположим, что это и были все друзья указанного пользователя (0).
Если глубина больше 1, то далее воспользуемся разностью множеств, первое из которых — значения словаря, а второе — его ключи. Таким образом, мы получим те id (в данном случае 0 и 4), которых нет в ключах, разобьем их опять на 25 частей и отправим хранимой процедуре.
Тогда в нашем словаре появятся 2 новых ключа:
{1:(0, 2, 3, 4), 2: (0, 1, 3, 4), 3: (0, 1, 2), 0: (1, 2, 3), 4:(1, 2, ….)}
Сам же метод deep_friends() выглядит следующим образом:
def deep_friends(self, deep): result = {} def fill_result(friends): for i in VkFriends.parts(friends): r = requests.get(self.request_url('execute.deepFriends', 'targets=%s' % VkFriends.make_targets(i))).json()['response'] for x, id in enumerate(i): result[id] = tuple(r[x]["items"]) if r[x] else None for i in range(deep): if result: # те айди, которых нет в ключах + не берем id:None fill_result(list(set([item for sublist in result.values() if sublist for item in sublist]) - set(result.keys()))) else: fill_result(requests.get(self.request_url('friends.get', 'user_id=%s' % self.my_id)).json()['response']["items"]) return result
Конечно, это быстрее, чем кидать по одному id в friends.get без использования хранимой процедуры, но времени все равно занимает порядочно много.
Если бы friends.get был похож на users.get, а именно мог принимать в качестве параметра user_ids, то есть перечисленные через запятую id, для которых нужно вернуть список друзей, а не по одному id, то код был бы намного проще, да и количество запросов было в разы меньше.
Слишком медленно
Возвращаясь к началу статьи, могу снова повторить — очень медленно. Хранимые процедуры не спасают, решение alxpy с многопоточностью (спасибо ему за вклад и участие
Мудрый совет получил от igrishaev — нужен какой-то мап-редьюс.
Дело в том, что ВКонтакте разрешает 25 запросов к API через execute, из этого следует, что если делать запросы с разных клиентов, то мы можем увеличить количество допустимых запросов. 5 тачек — это уже 125 запросов �� секунду. Но и это далеко не так. Забегая вперед, скажу, что можно и еще быстрее, примерно будет выглядеть следующим образом (на каждой машине):
while True: r = requests.get(request_url('execute.getMutual','source=%s&targets=%s' % (my_id, make_targets(lst)),access_token=True)).json() if 'response' in r: r = r["response"] break else: time.sleep(delay)
Если нам приходит сообщение об ошибке, то мы делаем запрос снова, спустя заданное количество секунд. Такой прием работает какое-то время, но затем ВКонтакте начинает присылать во всех ответах None, поэтому после каждого запроса честно будем ждать 1 секунду. Пока что.
Далее нам надо выбрать новые инструменты или же написать свои, чтобы реализовать задуманное. В итоге у нас должна получиться горизонтально масштабируемая система, принцип работы видится мне следующим образом:
- Главный сервер получает от клиента его id ВКонтакте и код операции: либо вытащить всех общих друзей, либо рекурсивно прогуляться по списку друзей с указанной глубиной.
- Далее в обоих случаях сервер делает запрос к API ВКонтакте — нам нужен список всех друзей пользователя.
- Поскольку все сделано для того, чтобы мы пользовались по-максимуму возможностями хранимых процедур — здесь надо будет разделить список друзей на части, по 25 контактов в каждой. На самом деле по 75. Об этом чуть ниже.
- У нас получится много частей, используя брокер сообщений будем доставлять каждую часть определенному получателю (producer-consumer).
- Получатели будут принимать контакты, сразу делать запросы, возвращать результат поставщику. Да, вы правильно подумали про RPC.
А если вы видели эту картинку, то понимаете, на какой брокер сообщений я намекаю.

Как только все ответы приняты, объединяем их в один. Далее результат можно будет вывести на экран или вовсе сохранить, об этом позже.
Тут стоит заметить, что код изменится, и если вам было достаточно использовать предыдущую версию проекта, то она так и осталась в неизменном виде. Весь код, который будет ниже, относится к новому релизу.
В качестве брокера сообщений будем использовать RabbitMQ, асинхронной распределенной очереди заданий — Celery.
Для тех, кто никогда с ними не сталкивался, вот несколько полезных ссылок на материалы, которые советую вам прочитать:
Celery
Не надо бояться понять, хоть и говорят, что можно конкретно повернуть свою голову, когда начинаешь «думать не одним компьютером, а несколькими», но это вовсе не так.
Если у вас Mac, как и у автора, то RabbitMQ шикарно ставится через Homebrew:
brew update brew install rabbitmq
Celery же ставится еще легче, используем третью ветку Python:
pip3 install Celery
У меня Celery установлен на Linux Mint, а RabbitMQ — на Mac. С виндой, как обычно, проблемы —
Далее создадим virtual host, пользователя и дадим ему права:
rabbitmqctl add_vhost vk_friends rabbitmqctl add_user user password rabbitmqctl set_permissions -p vk_friends user ".*" ".*" ".*"
В конфигурации RabbitMQ надо указать ip хоста, на котором он установлен:
vim /usr/local/etc/rabbitmq/rabbitmq-env.conf NODE_IP_ADDRESS=192.168.1.14 // конкретно мой вариант
Вот несколько возможных конфигураций, какую выбрать — решать вам.

Если у вас роутер или еще что-то, полезно будет знать, что RabbitMQ использует 5672 порт, ну и сделать переадресацию в настройках вашего устройства. Скорее всего, если будете тестировать, то воркеров раскидаете по разным машинам, а им нужно будет использовать брокер, и, если не правильно настроите сеть, Celery до RabbitMQ так и не достучится.
Очень хорошей новостью является то, что ВКонтакте разрешает делать по 3 запроса в секунду с одного id. Умножим эти запросы на количество возможных обращений к API ВКонтакте (25), получим максимальное число обрабатываемых контактов в секунду (75).

Если у нас будет много воркеров, то настанет момент, когда начнем переходить за дозволенный лимит. Поэтому переменная token (в settings.py) теперь будет кортежем, содержащим в себе несколько токенов с разных id. Скрипт же будет при каждом запросе к ВКонтакте API выбирать один из них рандомным образом:
def request_url(method_name, parameters, access_token=False): """read https://vk.com/dev/api_requests""" req_url = 'https://api.vk.com/method/{method_name}?{parameters}&v={api_v}'.format( method_name=method_name, api_v=api_v, parameters=parameters) if access_token: req_url = '{}&access_token={token}'.format(req_url, token=random.choice(token)) return req_url
В этом плане у вас не должно возникнуть сложностей, если есть несколько аккаунтов в ВКонтакте (можно напрячь друзей, родных), у меня не было проблем с 4 токенами и 3 воркерами.
Нет, вам никто не мешает использовать time.sleep(), или пример выше с while, но тогда готовьтесь получать сообщения об ошибках (возможны вообще пустые ответы — id:None), или подольше ждать.
Самое интересное из файла call.py:
def getMutual(): all_friends = friends(my_id) c_friends = group(mutual_friends.s(i) for i in parts(list(all_friends[0].keys()), 75))().get() result = {k: v for d in c_friends for k, v in d.items()} return cleaner(result) def getDeep(): result = {} for i in range(deep): if result: # те айди, которых нет в ключах + не берем id:None lst = list(set([item for sublist in result.values() if sublist for item in sublist]) - set(result.keys())) d_friends = group(deep_friends.s(i) for i in parts(list(lst), 75))().get() result = {k: v for d in d_friends for k, v in d.items()} result.update(result) else: all_friends = friends(my_id) d_friends = group(deep_friends.s(i) for i in parts(list(all_friends[0].keys()), 75) )().get() result = {k: v for d in d_friends for k, v in d.items()} result.update(result) return cleaner(result)
Как видите, в 2 функциях мы используем groups(), который параллельно запускает несколько заданий, после чего мы «склеиваем» ответ. Помните, как deep_friends() выглядел вначале (там уж очень старый при��ер — даже без многопоточности)? Смысл остался тем же — мы используем разность множеств.
И, наконец, tasks.py. Когда-нибудь эти замечательные функции объединятся в одну:
@app.task def mutual_friends(lst): """ read https://vk.com/dev/friends.getMutual and read https://vk.com/dev/execute """ result = {} for i in list(parts(lst, 25)): r = requests.get(request_url('execute.getMutual', 'source=%s&targets=%s' % (my_id, make_targets(i)), access_token=True)).json()['response'] for x, vk_id in enumerate(i): result[vk_id] = tuple(i for i in r[x]) if r[x] else None return result @app.task def deep_friends(friends): result = {} for i in list(parts(friends, 25)): r = requests.get(request_url('execute.deepFriends', 'targets=%s' % make_targets(i), access_token=True)).json()["response"] for x, vk_id in enumerate(i): result[vk_id] = tuple(r[x]["items"]) if r[x] else None return result
Когда все настроено, запускаем RabbitMQ командой:
rabbitmq-server
Затем переходим в папку проекта и активируем воркера:
celery -A tasks worker --loglevel=info
Теперь, чтобы получить и сохранить список общих или «глубинных» друзей, достаточно скомандовать в консоли:
python3 call.py
О результатах измерений
Напомню, что у автора статьи, которая вдохновила меня на первую часть, 343 друга (запрос на общих друзей) «обрабатывались» за 119 секунд.
Мой вариант из предыдущей статьи делал то же самое за 9 секунд.
Сейчас у того автора другое число друзей — 308. Что же, придется сделать один лишний запрос для последних восьми id, потратить на него драгоценную секунду, хотя за ту же секунду можно обработать 75 id.
С одним воркером работа скрипта заняла 4.2 секунды, с двумя воркерами — 2.2 секунды.
Если 119 округлим до 120, а 2.2 до 2, то мой вариант работает в 60 раз быстрее.
Что касается «глубинных друзей» (друзья моих друзей и так далее + тестируем на другом id, чтобы ждать меньше) — при глубине, равной 2, количество ключей в словаре составило 1 251.
Время выполнение кода, приведенного в самом начале статьи, — 17.9 секунды.
Одним воркером время выполнения скрипта — 15.1 секунды, с двумя воркерами — 8.2 секунды.
Таким образом, deep_friends() стал быстрее примерно в 2.18 раза.
Да, не всегда результат такой радужный, иногда ответа на один запрос в ВКонтакте приходится ждать и по 10, и по 20 секунд (хотя частое время выполнения одного задания 1.2 — 1.6 секунд), скорее всего, это связано с нагрузкой на сервис, ведь мы не одни во вселенной.

В итоге, чем больше воркеров сделать, тем быстрее будет обрабатываться результат. Не забудьте про мощность своего железа, дополнительные токены, сеть (например, у автора резко возрастало время выполнения скрипта, когда он юзал свой айфон в качестве точки доступа) и иные факторы.
Сохранение результата
Да, есть много графо-ориентированных БД. Если в дальнейшем (а оно так и будет), мы захотим анализировать полученные результаты, то все равно их надо будет где-то хранить до самого анализа, потом эти же результаты выгружать в память и производить с ними какие-нибудь действия. Не вижу смысла использовать какую-нибудь субд, если проект был бы коммерческим и нас интересовало, например, что происходит с графом конкретного пользователя на протяжении времени — то да, тут обязательна графо-ориентированная бд, но, поскольку заниматься анализом будем в «домашних условиях», pickle нам хватит вполне.
Перед сохранением словарей логично будет удалять из них ключи, значения которых None. Это заблокированные или удаленные аккаунты. Проще говоря, эти id будут присутствовать в графе, потому что они есть у кого-то в друзьях, ну а мы сэкономим на количестве ключей в словаре:
def cleaner(dct): return {k:v for k, v in dct.items() if v != None} def save_or_load(myfile, sv, smth=None): if sv and smth: pickle.dump(smth, open(myfile, "wb")) else: return pickle.load(open(myfile, "rb"))
Как видно, если мы где-то сохранили результат, то где-то и должны его загрузить, дабы заново не собирать id.
Анализ графа
Чтобы не писать свой велосипед, воспользуемся довольно известным networkx, который сделает за нас всю
pip3 install networkx
Прежде чем начнем анализировать граф, нарисуем его. networkx для этого понадобится matplotlib:
pip3 install matplotlib
Далее нам надо создать сам граф. Вообще, есть 2 пути.
Первый сожрет много оперативной памяти и вашего времени:
def adder(self, node): if node not in self.graph.nodes(): self.graph.add_node(node) self.graph = nx.Graph() for k, v in self.dct.items(): self.adder(k) for i in v: self.adder(i) self.graph.add_edge(k, i)
И это не автор выжил из ума, нет. Подобный пример приводится на странице университета Райса (Rice University), под заголовком Convert Dictionary Graph Representation into networkx Graph Representation:
def dict2nx(aDictGraph): """ Converts the given dictionary representation of a graph, aDictGraph, into a networkx DiGraph (directed graph) representation. aDictGraph is a dictionary that maps nodes to its neighbors (successors): {node:[nodes]} A DiGraph object is returned. """ g = nx.DiGraph() for node, neighbors in aDictGraph.items(): g.add_node(node) # in case there are nodes with no edges for neighbor in neighbors: g.add_edge(node, neighbor) return g
Можете поверить мне на слово, граф строился целый вечер, когда в нем было уже более 300 000 вершин, мое терпение лопнуло.
Да, приводится пример для ориентированного графа, но суть остается той же — сначала добавляем ключи, делая их вершинами, потом делаем вершинами значения, и то если их еще нет в графе, а потом соединяем их ребрами (в моем варианте).
А второй способ сделает все за секунды:
self.graph = nx.from_dict_of_lists(self.dct)
Код лежит в файле graph.py, чтобы нарисовать граф общих друзей достаточно запустить этот скрипт или же где-нибудь создать экземпляр класса VkGraph(), а затем вызвать его метод draw_graph().

Это граф общих друзей, всего 306 вершин и 2096 ребер. К сожалению, я ни разу не дизайнер (практически все настройки стандартные), но вы всегда сможете стилизовать граф «под себя». Вот пара ссылок:
А сам метод выглядит так:
def draw_graph(self): plt.figure(figsize=(19,19), dpi=450,) nx.draw(self.graph, node_size=100, cmap=True) plt.savefig("%s graph.png" % datetime.now().strftime('%H:%M:%S %d-%m-%Y'))
В итоге вы получаете картинку date graph.png в папке проекта. Не советую рисовать граф для глубинных друзей. При 308 друзьях и глубиной равной 2, в словаре оказалось более 145 000 ключей. А есть ведь еще и значения — кортежи с id, которых вряд ли будет мало.
Долго искал самый малосодержащий друзей профиль в ВКонтакте, хотя тут важнее — друзья-друзей. 10 начальных друзей (1 из них заблокированный и автоматически удалится), при нашей стандартной глубине (2), в словаре насчитывалось 1234 ключа и 517 174 id (из значений). Примерно 419 друзей у одного id. Да, там есть и общие друзья, когда построим граф, мы это поймем:
deep_friends = VkGraph(d_friends_dct) print('Количество вершин:', deep_friends.graph.number_of_nodes()) print('Количество ребер:', deep_friends.graph.number_of_edges())
Вернет:
Количество вершин: 370341 Количество ребер: 512949
С такими большими данными было бы неплохо поиграться. У networkx очень большой список алгоритмов, которые можно применять к графам. Разберем некоторые из них.
Связный граф
Для начала определим, связный ли у нас граф:
print('Связный граф?', nx.is_connected(deep_friends.graph))
Связный граф — это такой граф, в котором любая пара вершин соединена маршрутом.
Кстати, у того же самого id при глубине, равной 1, вот такой красивый граф, содержащий 1268 вершин и 1329 ребер:

Вопрос знатокам. Раз у нас получается граф друзья-друзей, он по-любому должен быть связным. Не может быть такого, чтобы из ниоткуда появлялась вершина, которая не связана ни с одной из существующих. Однако мы видим справа одну вершину, которая не соединена ни с одной. Почему? Призываю сначала подумать, интереснее будет узнать истину.
Правильный ответ
Давайте разберемся. Сначала берется список друзей, и получается так, что есть у нас id X. Из-за которого граф несвязный. Далее мы делаем запрос на друзей этого X (в глубину ведь). Так вот если у X все друзья скрытые, то будет запись в словаре:
Когда будет строится граф, мы честно добавим вершину X, но никаких ребер у нее не будет. Да, чисто теоретически у вершины X должно быть ребро с вершиной, id которой указан в settings.py, но вы же внимательно читали — мы добавляем только то, что находится в словаре. Следовательно, при глубине, равной 2, мы получим в словаре id, указанный в настройках. И тогда у вершины X появятся ребра.
{X:(), ...}
Когда будет строится граф, мы честно добавим вершину X, но никаких ребер у нее не будет. Да, чисто теоретически у вершины X должно быть ребро с вершиной, id которой указан в settings.py, но вы же внимательно читали — мы добавляем только то, что находится в словаре. Следовательно, при глубине, равной 2, мы получим в словаре id, указанный в настройках. И тогда у вершины X появятся ребра.
Будем считать, что у вас не будет такой ситуации, то есть скорее всего вы увидите True.
Диаметр, центр и радиус
Вспомним, что диаметром графа называется максимальное расстояние между двумя его вершинами.
print('Диамерт графа:', nx.diameter(deep_friends.graph))
Центр графа — это любая вершина, такая, что расстояние от нее до наиболее отдаленной вершины минимально. Центром графа может быть одна вершина или несколько вершин. Или проще. Центр графа — вершина, эксцентриситет (расстояние от этой вершины до самой удаленной от нее) которой равен радиусу.
print('Центр графа:', nx.center(deep_friends.graph))
Вернет список вершин, которые являются центром графа. Не удивляйтесь, если центром окажется id, указанный в settings.py.
Радиус графа — это наименьший из эксцентриситетов всех вершин.
print('Радиус графа:', nx.radius(deep_friends.graph))
Авторитетность или Page Rank
Этот тот самый Page Rank, о котором вы подумали. Как правило, алгоритм используется для веб-страничек или иных документов, связанных ссылками. Чем больше ссылок на страницу, тем она важнее. Но никто не запрещает использовать этот алгоритм для графов. Более точное и подходящее определение позаимствуем из этой статьи:
Авторитетность в социальном графе можно анализировать разными способами. Самый простой — отсортировать участников по количеству входящих ребер. У кого больше — тот больше авторитетен. Такой способ годен для небольших графов. В поиске по Интернету Google в качестве одного из критериев для авторитетности страниц использует PageRank. Он вычисляется при помощи случайного блуждания по графу, где в качестве узлов — страницы, а ребро между узлами — если одна страница ссылается на другую. Случайный блуждатель двигается по графу и время от времени перемещается на случайный узел и начинает блуждание заново. PageRank равен доли пребывания на каком-то узле за все время блуждания. Чем он больше, тем узел более авторитетен.
import operator print('Page Rank:', sorted(nx.pagerank(deep_friends.graph).items(), key=operator.itemgetter(1), reverse=True))
Коэффициент кластеризации
Цитируя Википедию:
Коэффициент кластеризация — это степень вероятности того, что два разных пользователя, связанные с конкретным индивидуумом, тоже связаны.
print('Коэффициент кластеризации', nx.average_clustering(deep_friends.graph))
Как видите, нет ничего сложного, и networkx предлагает еще много алгоритмов (автор насчитал 148), которые можно применять к графам. Вам остается лишь выбрать нужный вам алгоритм и вызвать соответствующий метод в файле graph.py.
Итог
Мы сделали распределенную систему, позволяющую собирать и строить граф общих друзей в ВКонтакте, которая работает в 60 раз быстрее (в зависимости от количества воркеров), чем предложенный вариант от Himura, также реализовали новую функцию — запрос всех «глубинных друзей», добавили возможность анализа построенных графов.
Если вы не хотите ставить дополнительное ПО и вам надо построить красивый граф общих друзей из предыдущей статьи, то старый релиз к вашим услугам. В нем вы также найдете старую версию получения списка друзей пользователя рекурсивно сколь угодно глубоко.
Это вовсе не предел, будут продолжаться работы по увеличению быстродействия программы.
По-прежнему жду от вас вкусных пулл-реквестов, особенно если вы занимаетесь визуализированием данных. Спасибо за внимание!
