maisvendoo 10 авг 2015 в 02:09

Метод функций Ляпунова в задаче об эффекте Джанибекова

8 мин

22K

Введение

Данная статья не имеет отношения к циклу «Магия тензорной алгебры», но вызвана к жизни публикациями из него. Небрежно щелкая по ссылкам в поисковике набрел на обсуждение одной из своих статей, посвященных эффекту Джанибекова, и обратил внимание на справедливое замечание о том, что исследование устойчивости гайки Джанибекова по первому приближению не дает однозначного ответа на вопрос о том при каких параметрах движение будет устойчивым. Это так, поскольку корни характеристического полинома, при вращении вокруг оси с наименьшим и наибольшим моментом инерции чисто мнимые, их действительная часть равна нулю. При таких условиях нельзя ответить на вопрос будет ли движение устойчивым, не проведя дополнительного исследования.

Интерпретация Мак-Куллага — наверно самое простое объяснение эффекта Джанибекова

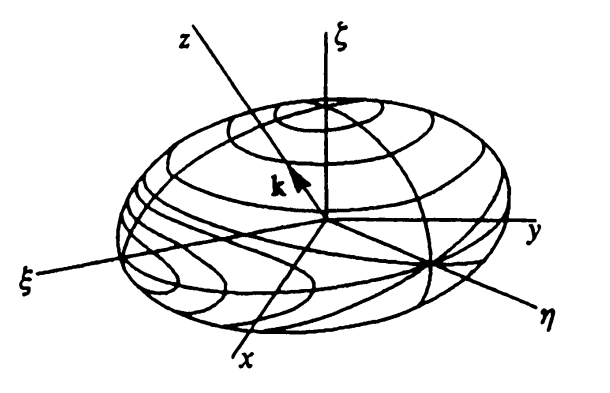
Такое исследование можно выполнить используя метод функций Ляпунова (второй или прямой метод Ляпунова). И чтобы окончательно закрыть вопрос с гайкой Джанибекова, я решил написать эту заметку.

1.Дифференциальные уравнения возмущенного движения. Снова.

Пусть имеется система, в общем случае нелинейных дифференциальных уравнений движения некоторой механической системы

$\frac{d\mathbf y}{dt} = \mathbf F(t, \, \mathbf y)$

где $\mathbf y = \begin{bmatrix} y_1 && y_2 && \cdots && y_n \end{bmatrix}^T$ — вектор-столбец переменных состояния системы; $\mathbf F(t, \, \mathbf y)$ — нелинейная вектор функция.

Решение системы (1) $\mathbf y(t) = \mathbf y_0(t)$ дает так называемое невозмущенное движение. По сути это обычный, установившийся режим движения системы под действием приложенных к ней сил. Зададим некоторое возмущение, определяемое вектором $\mathbf x(t)$ отклонений от невозмущенного движения, то есть

$\mathbf y(t) = \mathbf y_0(t) + \mathbf x(t)$

Подставляя (3) в (1), получаем

$\frac{d\mathbf y_0}{dt} + \frac{d\mathbf x}{dt} = \mathbf F(t, \, \mathbf y_0 + \mathbf x)$

Вычтем (1) из (4)

$\frac{d\mathbf x}{dt} = \mathbf F(t, \, \mathbf y_0 + \mathbf x) - \mathbf F(t, \, \mathbf y_0)$

или

$\frac{d\mathbf x}{dt} = \mathbf G(t, \, \mathbf x)$

где $\mathbf G(t, \, \mathbf x) = \mathbf F(t, \,\mathbf y_0 + \mathbf x) - \mathbf F(t, \,\mathbf y_0)$ , и полученное уравнение называется уравнением возмущенного движения, тривиальное решение которого $x_1 = x_2 = ... = x_n = 0$ соответствует невозмущенному движению системы.

В нашем случае ограничимся рассмотрением автономной системы, где правая часть явно не зависит от времени

$\frac{d\mathbf x}{dt} = \mathbf G(\mathbf x)$

2. Xитрая функция V(x) — кандидат в функции Ляпунова

Рассмотрим некоторую скалярную функцию

$V = V(\mathbf x) = V(x_1, \, x_2, \, ...,\, x_n)$

определенную в некоторой окрестности начала координат, такой что

$|x_i| < h, \quad i = \overline{1,n}$

где $h$ — некоторое, достаточно малое, положительное число.

Функция (6) называется знакоопределенной, если в области (7) она принимает значения только одного знака (только положительные либо только отрицательные), и равна нулю лишь в начале координат (при $x_1 = x_2 = ... = x_n = 0$ )

Функция (6) называется знакопостоянной, если в области (7) она принимает значения только одного определенного знака, но может обращаться в нуль и при $x_1^2 + x_2^2 + ... + x_n^2 \ne 0$ .

Вычислим полную производную от функции (6) по времени. Так как $x_i = x_i(t), \quad i = \overline{1,n}$ , по определению полной производной получаем

$\frac{dV}{dt} = \sum_{i=1}^n \frac{\partial V}{\partial x_i} \, \dot x_i$

что, принимая во внимание уравнение (5), эквивалентно соотношению

$\frac{dV}{dt} = \sum_{i=1}^n \frac{\partial V}{\partial x_i} \, G_i(x_1, \, x_2, \, ..., \, x_n)$

Функцию (8) называют полной производной функции (6) по времени, составленной в силу уравнения (5).

3. Теоремы Ляпунова об устойчивости

Два параграфа, что выше, написаны сухим математическим языком определений, и иначе наверное нельзя. Добавим ещё немного формальной математики, сформулировав

Теорема Ляпунова об устойчивости

Если для системы уравнений (5) существует знакоопределённая функция $V(x_1, \, x_2, \, ...,\, x_n)$ (функция Ляпунова), полная производная по времени которой, составленная в силу системы (5) есть функция знакопостоянная, знака, противоположного V, либо тождественно равная нулю, то точка покоя системы (5) $x_1 = x_2 = ... = x_n = 0$ устойчива

Под точкой покоя системы (5) здесь понимается её тривиальное решение, соответствующее невозмущенному движению рассматриваемой механической системы. Грубо говоря, согласно сформулированной теореме, следует подобрать функцию $V(x_1, \, x_2, \, ...,\, x_n)$ , удовлетворяющую свойствам, указанным в условии теоремы. Если она удовлетворяет данным свойствам, то её называют функцией Ляпунова, и если таковая функция (хотя бы одна!) существует, то установившийся режим движения рассматриваемой механической системы будет устойчивым.

Однако, в данной теореме не идёт речь об асимптотической устойчивости, то есть таком характере движения системы, при котором возмущенное её движение будет стремится к исходному установившемуся режиму. Под устойчивым здесь понимается и такое движение, при котором система будет колебаться в окретсности исходного установившегося режима, но никогда к нему не вернется. Условие асимптотической устойчивости будет более строгим

Теорема Ляпунова об асимптотической устойчивости

Если для системы уравнений (5) существует знакоопределённая функция $V(x_1, \, x_2, \, ...,\, x_n)$ (функция Ляпунова), полная производная по времени которой, составленная в силу системы (5) есть функция знакоопределенная, знака, противоположного V, то точка покоя системы (5) $x_1 = x_2 = ... = x_n = 0$ асимптотически устойчива

Асимптотически устойчивая система, после возмущения, будет стремится вернуться к установившемуся режиму движения, то есть решение системы (5) будет сходится к началу координат $x_i = 0, \quad i=\overline{1,n}$ .

Эти теоремы дают путь к исследованию устойчивости линейных и нелинейных механических систем, более общий, чем исследование по первому приближению.

Другой вопрос, как найти функцию Ляпунова, удовлетворяющую уравнению (5) и требованиям теорем. Однозначного ответа на этот вопрос математика ещё не знает. Есть ряд работ, всецело посвященных этому вопросу, например книга Е. А. Барабашина «Функции Ляпунова». Для большинства линейных систем можно искать функции Ляпунова в виде квадратичных форм, например, для системы третьего порядка эта функция может быть такой

$V = x_1^2 + x_2^2 + x_3^2$

данная функция — определенно-положительная, причем в сколь угодно большой окрестности точки покоя системы. Или такая функция

$V = x_1^2 + x_2^2 + 2 \, x_1 \, x_2 + x_3^2$

будет знакопостоянной, положительной, ибо $V = (x_1 + x_2)^2 + x_3^2$ может быть равна нулю как в точке покоя системы $x_1 = x_2 = x_3 = 0$ , так и в точке, удовлетворяющей условию $x_3 = 0, \quad x_1 = -x_2$ .

В случае консервативных механических систем функцией Ляпунова может служить полная механическая энергия системы, которая, при отсутствии диссипации, является константой (знакопостоянна) и ещё производная по времени равная нулю — она ведь константа. И вытекает эта функция из системы уравнений движения, ибо является одним из её интегралов.

В случае с гайкой Джанибекова, в качестве весьма элегантного решения мной взята идея из книги А. П. Маркеева «Теоретическая механика». Это решение несколько переработано и расширено мной, чтобы быть в контексте ранее написанных статей.

4. Интегралы движения гайки Джанибекова

Получим два первых интеграла движения, опираясь на систему уравнений, приведенную в тензорном цикле. Оперировать будем тензорными соотношениями, чтобы не терять хватки. Итак, уравнение вращения гайки вокруг центра масс имеет вид

$I_{\,j}^{\,i} \, \dot\omega^{j} + \varepsilon^{\,ijk} \, \omega_{\,j} \, g_{\,kl} \, I_{\,p}^{\,l} \, \omega^{\,p} = 0$

перейдем в данном уравнении к вектору МКД

$\dot L^{\,i} + \varepsilon^{\,ijk} \, \omega_{\,j} \, L_{\,k} = 0$

Умножим уравнение (10) скалярно на удвоенный вектор МКД

$2\, L_{\,i} \, \frac{dL^{\,i}}{dt} + 2\, \varepsilon^{\,ijk} \, L_{\,i} \, L_{\,k} \, \omega_{\,j} = 0$

Нетрудно заметить, что во втором слагаемом (11) свертка $\varepsilon^{\,ijk} \, L_{\,i} \, L_{\,k} = 0$ , а в первом — производная от квадрата модуля МКД. Преобразуем уравнение (11) и проинтегрируем его

$\begin{align*} &\frac{d}{dt} \left( L^{\,2} \right) = 0 \\ &L^{\,2} = \rm const \end{align*}$

или

$I_x^{\,2} \, \omega_x^2 + I_y^{\,2} \, \omega_y^2 + I_z^{\,2} \, \omega_z^2 = \rm const$

Выражение (12) есть первый интеграл движения, выражающий постоянство модуля МКД рассматриваемой нами гайки. Чтобы получить ещё один первый интеграл движения, умножим (9) скалярно на вектор угловой скорости

$\omega_{\,i} \, I_{\,j}^{\,i} \, \dot\omega^{j} + \varepsilon^{\,ijk} \, \omega_{\,i} \, \omega_{\,j} \, g_{\,kl} \, I_{\,p}^{\,l} \, \omega^{\,p} = 0$

после чего, внезапно, обнаруживаем во втором слагаемом свертку $\varepsilon^{\,ijk} \, \omega_{\,i} \, \omega_{\,j}$ равную нулю, получая уравнение

$\omega_{\,i} \, I_{\,j}^{\,i} \, \dot\omega^{j} = 0$

Вспомним, ведь что-то похожее мы уже видели ранее. Ведь кинетическая энергия тела в его вращении относительно центра масс равна

$T = \frac{1}{2} \, \omega_i \, I_j^i \, \omega^{\,j}$

и если мы продифференцируем её по времени, что получим

$\frac{dT}{dt} = \frac{1}{2} \, \dot\omega_i \, I_j^i \, \omega^{\,j} + \frac{1}{2} \, \omega_i \, I_j^i \, \dot\omega^{\,j} = \omega_i \, I_j^i \, \dot\omega^{\,j}$

в соответствии с этим, мы можем переписать уравнение (13) и проинтегрировать его

$\begin{align*} &\frac{d}{dt} \, \left( \frac{1}{2} \, \omega_i \, I_j^i \, \omega^{\,j} \right) = 0 \\ &\frac{1}{2} \, \omega_i \, I_j^i \, \omega^{\,j} = \rm const \end{align*}$

Учитывая, что умножение константы на двойку не меняет её «константности», можно окончательно записать первый интеграл в компонентной форме (учитывая декартов базис!)

$I_x \, \omega_x^2 + I_y \, \omega_y^2 + I_z \, \omega_z^2 = \rm const$

Выражение (14) выражает постоянство кинетической энергии вращения гайки вокруг центра масс. Осталось перейти в выражениях (12) и (14) к безразмерным моментам инерции $i_y = \frac{I_y}{I_x}, \quad i_z = \frac{I_z}{I_x}$

$\begin{align*} &\omega_x^2 + i_y^{\,2} \, \omega_y^2 + i_z^{\,2} \, \omega_z^2 = \rm const \\ &\omega_x^2 + i_y \, \omega_y^2 + i_z \, \omega_z^2 = \rm const \end{align*}$

Полученные уравнения и есть те первые интегралы движения, которые мы используем для построения функции Ляпунова

4. Построение функции Ляпунова из интегралов движения

Метод построения функции Ляпунова из уравнений вида (15) носит название метода интегральных связок Четаева и говорит о том, что означенную функцию можно искать в виде связки интегралов движения вида

$V = \lambda_1 \, U_1 + \lambda_2 \, U_2 + ... + \lambda_k \, U_k + \mu_1 \, U_1^2 + \mu_2 \, U_2^2 + ... + \mu_k \, U_k^2$

где $U_1,...,U_k$ — первые интегралы уравнений возмущенного движения; $\lambda_1,...,\lambda_k$ и $\mu_1,...,\mu_k$ — неопределенные константы, подбором которых можно сделать функцию (16) определенно положительной, удовлетворяющей теореме Ляпунова об устойчивости.

Невозмущенное вращение гайки происходит вокруг оси $x$ с постоянной угловой скоростью $\omega$ . Возмутим это движение, дав угловой скорости малое приращение $\Delta\vec\omega$ , и перепишем выражения (15)

$\begin{align*} &(\omega + \Delta\omega_x)^2 + i_y^{\,2} \, \Delta\omega_y^2 + i_z^{\,2} \, \Delta\omega_z^2 = \rm const \\ &(\omega + \Delta\omega_x)^2 + i_y \, \Delta\omega_y^2 + i_z \, \Delta\omega_z^2 = \rm const \end{align*}$

или

$\begin{align*} &\omega^2 + 2\omega \, \Delta\omega_x + \Delta\omega_x^2 + i_y^{\,2} \, \Delta\omega_y^2 + i_z^{\,2} \, \Delta\omega_z^2 = \rm const \\ &\omega^2 + 2\omega \, \Delta\omega_x + \Delta\omega_x^2 + i_y \, \Delta\omega_y^2 + i_z \, \Delta\omega_z^2 = \rm const \end{align*}$

При установившемся вращении гайки с постоянной угловой скоростью, константу $\omega^2$ можно вычесть из обоих частей получившихся уравнений, получив в их левой части функции

$\begin{align*} &U_1 = \Delta\omega_x^2 + i_y^{\,2} \, \Delta\omega_y^2 + i_z^{\,2} \, \Delta\omega_z^2 + 2\omega \, \Delta\omega_x \\ &U_2 = \Delta\omega_x^2 + i_y \, \Delta\omega_y^2 + i_z \, \Delta\omega_z^2 + 2\omega \, \Delta\omega_x \end{align*}$

Функция Ляпунова будет иметь вид

$V = U_1^2 + U_2^2$

Исходя из уравнений (15) понятно, что $\frac{dV}{dt} = 0$ , значит об асимптотической устойчивости речи не будет. Но, исходя из теоремы Ляпунова, необходимо убедится в том, что функция (18) определенно-положительна. Из выражений (18) и (17) понятно, что её значения положительны при любых $\Delta\omega_x$ , $\Delta\omega_y$ и $\Delta\omega_z$ . Теперь покажем, что (18) обращается в нуль только в точке покоя системы $\Delta\omega_x = \Delta\omega_y = \Delta\omega_z = 0$ . Выражение (18) равно нулю исключительно в случае

$U_1 = 0, \quad U_2 = 0$

Из первого уравнения системы (19) вычтем второе

$U_1 - U_2 = i_y \left( 1 - i_y \right) \, \Delta\omega_y^2 + i_z \left( 1 - i_z \right) \, \Delta\omega_z^2 = 0$

Если $i_y, \, i_z < 1$ (момент инерции, вокруг которого вращается гайка наибольший), или же $i_y, \, i_z > 1$ (момент инерции, вокруг которого вращается гайка наименьший), то равенство (20) будет справедливо лишь в случае когда $\Delta\omega_y = \Delta\omega_z = 0$ . Учтем данный факт и сложим уравнения (19)

$U_1 + U_2 = 2 \, \Delta\omega_x^2 + 4\,\omega \, \Delta\omega_x = 2\,\Delta\omega_x \left(\Delta\omega_x + 2\,\omega \right) = 0$

Уравнение (21) справедливо при $\Delta\omega_x = 0$ и при $\Delta\omega_x = - 2 \, \omega$ . Но, так как мы полагаем $|\Delta\omega_x| \ll 2\,\omega$ , функция (18) будет равна нулю исключительно в точке покоя системы $\Delta\omega_x = \Delta\omega_y = \Delta\omega_z = 0$ .

Таким образом, вращение гайки вокруг оси с наименьшим и наибольшим моментом инерции будет устойчивым по Ляпунову.

Однако, спешу заметить, что при $i_y > 1, \quad i_z < 1$ , или $i_y < 1, \quad i_z > 1$ , то есть когда момент инерции относительно оси, вокруг которой происходит вращение имеет промежуточное между максимальным и минимальным значение, функцию (18) уже нельзя назвать определенной положительно, из-за того что слагаемые в (20) будут иметь разные знаки. Но совершенно нельзя сказать о том, что движение будет неустойчивым. Особенность теорем Ляпунова об устойчивости в том, что они декларируют условие устойчивости, но не декларируют обратного. Неустойчивость движения придется доказывать отдельно.

5. Неустойчивость вращения гайки Джанибекова

Сформулируем определение

Областью $v > 0$ будем называть какую либо область окрестности $|x_i| < h, \quad i = \overline{1,n}$ , где для некоторой функции $v(x_1, x_2,...,x_n)$ выполняется условие $v(x_1, x_2,...,x_n) > 0$ , причем на границе области $v = 0$ и точка покоя системы принадлежит этой границе.

и теорему

Теорема Четаева о неустойчивости

Если дифференциальные уравнения возмущенного движения (5) таковы, что существует функция $v(x_1, x_2,...,x_n)$ , такая, что в сколь угодно малой окрестности

$|x_i| < h, \quad i = \overline{1,n}$

существует область $v > 0$ , и во всех точках этой области производная $\dot v$ в силу уравнений (5) принимает положительные значения, то невозмущенное движение неустойчиво.

Функция $v(x_1, x_2,...,x_n)$ о которой говорится в теореме называется функцией Четаева. Теперь рассмотрим снова нашу гайку, уравнения вращения которой выглядят так (с учетом работы в связанных с телом декартовых координатах и введенных нами безразмерных моментов инерции)

$\begin{align*} &\dot\omega_x = \left(i_y - i_z) \, \omega_y \, \omega_z \\ &\dot\omega_y = \frac{i_z - 1}{i_y} \, \omega_x \, \omega_z \\ &\dot\omega_z = \frac{1 - i_y}{i_z} \, \omega_x \, \omega_y \end{align*}$

Учитывая, что изначально вращение происходит с постоянной угловой скоростью $\omega$ вокруг оси $x$ , построим уравнения возмущенного движения. Будем считать, что $\omega > 0$ — этого всегда можно добиться выбором осей собственной системы координат.

$\begin{align*} &\Delta\dot\omega_x = \left(i_y - i_z) \, \Delta\omega_y \, \Delta\omega_z \\ &\Delta\dot\omega_y = \frac{i_z - 1}{i_y} \, (\omega + \Delta\omega_x) \, \Delta\omega_z \\ &\Delta\dot\omega_z = \frac{1 - i_y}{i_z} \, (\omega + \Delta\omega_x) \, \Delta\omega_y \end{align*}$

Построим функцию Четаева

$v = \Delta\omega_y \, \Delta\omega_z$

Точка покоя системы лежит на границе $v > 0$ , а функция (23) положительна при $\Delta\omega_y, \, \Delta\omega_z > 0$ . Производная по времени от (23) в силу (22) имеет вид

$\dot v = \Delta\dot\omega_y \, \Delta\omega_z + \Delta\omega_y \, \Delta\dot\omega_z = (\omega + \Delta\omega_x) \, \left(\frac{i_z - 1}{i_y} \, \Delta\omega_z^2 + \frac{1 - i_y}{i_z} \, \Delta\omega_y^2 \right)$

В силу того, что $\omega > 0, \quad \omega \gg |\Delta\omega_x|$ , а так же при условии вращения гайки вокруг среднего момента инерции, так что $i_z > 1, \quad i_y < 1$ , то есть $I_z > I_x > I_y$ , производная (24) положительна в области $v > 0$ , а значит движение будет неустойчивым.

Если же, как в рассматриваемом нами изначально случае, $I_y > I_x > I_z$ , или $i_z < 1, \quad i_y > 1$ , то в качестве функции Четаева выберем

$v = -\Delta\omega_y \, \Delta\omega_z$

Тогда область $v > 0$ соответствует условию $\Delta\omega_y, \, \Delta\omega_z < 0$ , точка покоя системы так же лежит на её границе, а производная (25), равная

$\dot v = -\Delta\dot\omega_y \, \Delta\omega_z - \Delta\omega_y \, \Delta\dot\omega_z = (\omega + \Delta\omega_x) \, \left(\frac{1 - i_z}{i_y} \, \Delta\omega_z^2 + \frac{i_y - 1}{i_z} \, \Delta\omega_y^2 \right)$

так же будет положительна. Движение будет неустойчивым.

Заключение

Данная статья — дополнение к статье об устойчивости движения гайки Джанибекова. Основной материал взят из приведенных выше литературных источников, а так же сайта Math Help Planet. Авторский вклад в эту статью — поэтапное подробное рассмотрение второго метода Ляпунова на примере конкретной задачи. Кроме того, чуть более развернуто, чем в книге Маркеева, рассмотрен вопрос о неустойчивости движения применительно к различным вариантам соотношения между моментами инерции гайки.

Таким образом считаю, что я исправил недочет, связанный с неполнотой изложения вопроса о причинах эффекта Джанибекова. А заодно и сам подробнее изучил второй метод Ляпунова.

Благодарю читателей за проявленное внимание!

Теги:

Хабы:

Математика