В июне этого года в России был принят новый стандарт блочного шифрования — ГОСТ Р 34.12-2015. Этот стандарт помимо старого доброго ГОСТ 28147-89, который теперь называется «Магма» и имеет фиксированный набор подстановок, содержит описание блочного шифра «Кузнечик». О нем я и расскажу в этом посте.
В отличие от ГОСТ 28147-89 новый шифр представляет собой не сеть Фейстеля, а т.н. SP-сеть: преобразование, состоящее из нескольких одинаковых раундов, при этом каждый раунд состоит из нелинейного и линейного преобразований, а также операции наложения ключа. В отличие от сети Фейстеля, при использовании SP-сети преобразуется весь входной блок, а не его половина. Такая структура иногда также называется AES-like (похожей на AES), однако, в отличие от последнего у «Кузнечика» есть ряд своих «фишек»:
Длина входного блока «Кузнечика» — 128 бит, ключа — 256 бит.
Шифрование основано на последовательном применении нескольких однотипных раундов, каждый из которых содержит три преобразования: сложение с раундовым ключом, преобразование блоком подстановок и линейное преобразование.
128-битный входной вектор очередного раунда складывается побитно с раундовым ключом:
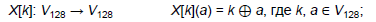
Нелинейное преобразование представляет собой применение к каждому 8-битному подвектору 128-битного входного вектора фиксированной подстановки:
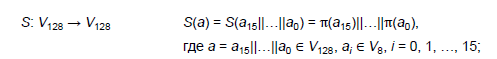
В «Кузнечике» используется та же подстановка, что и в хэш-функции «Стрибог».
Линейное преобразование, как я уже сказал, может быть реализовано не только как обычно в блочных шифрах — матрицей, но и с помощью РСЛОС — линейного регистра сдвига с обратной связью, который движется 16 раз.

Сам регистр реализуется над полем Галуа по модулю неприводимого многочлена степени 8: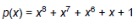 :
:

Раундовое преобразование можно изобразить следующим образом:
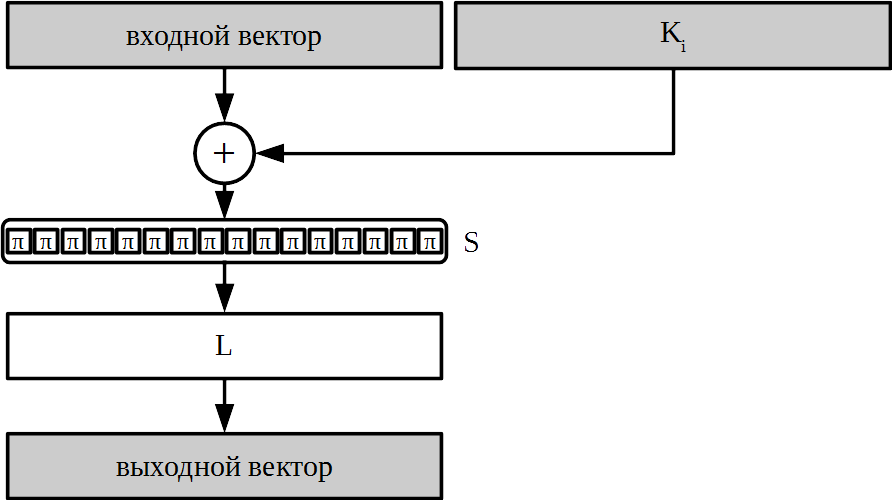
Рассмотрим теперь процедуру генерации раундовых ключей из мастер-ключа. Первые два получаются разбиением мастер-ключа пополам. Далее для выработки очередной пары раундовых ключей используется 8 итераций сети Фейстеля, где, в свою очередь, в качестве раундовых ключей используется счетчиковая последовательность, прошедшая через линейное преобразование алгоритма:
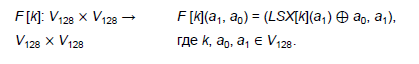

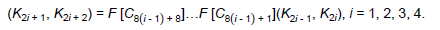
Раунд ключевой развертки можно представить следующим образом:

А всю процедуру выработки раундовых ключей так:

В результате, шифрование одного 128-битного входного блока описывается следующим уравнением:
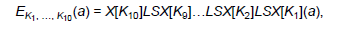
А в виде блок-схемы может быть представлено так:
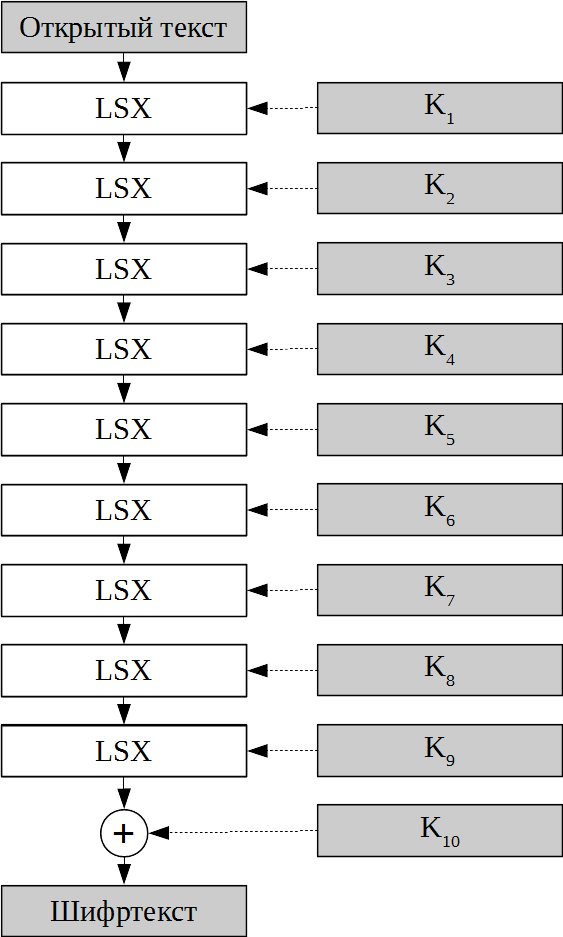
Расшифрование реализуется обращением базовых преобразований и применением их в обратном порядке:

В отличие от ГОСТ 28147-89 новый шифр представляет собой не сеть Фейстеля, а т.н. SP-сеть: преобразование, состоящее из нескольких одинаковых раундов, при этом каждый раунд состоит из нелинейного и линейного преобразований, а также операции наложения ключа. В отличие от сети Фейстеля, при использовании SP-сети преобразуется весь входной блок, а не его половина. Такая структура иногда также называется AES-like (похожей на AES), однако, в отличие от последнего у «Кузнечика» есть ряд своих «фишек»:
- линейное преобразование может быть реализовано в с помощью регистра сдвига;
- ключевая развертка реализована с помощью сети Фейстеля, в которой в качестве функции используется раундовое преобразование исходного алгоритма.
Длина входного блока «Кузнечика» — 128 бит, ключа — 256 бит.
Преобразования
Шифрование основано на последовательном применении нескольких однотипных раундов, каждый из которых содержит три преобразования: сложение с раундовым ключом, преобразование блоком подстановок и линейное преобразование.
128-битный входной вектор очередного раунда складывается побитно с раундовым ключом:
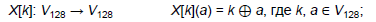
Нелинейное преобразование представляет собой применение к каждому 8-битному подвектору 128-битного входного вектора фиксированной подстановки:
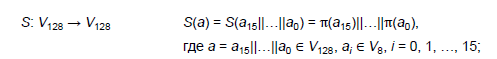
В «Кузнечике» используется та же подстановка, что и в хэш-функции «Стрибог».
Линейное преобразование, как я уже сказал, может быть реализовано не только как обычно в блочных шифрах — матрицей, но и с помощью РСЛОС — линейного регистра сдвига с обратной связью, который движется 16 раз.

Сам регистр реализуется над полем Галуа по модулю неприводимого многочлена степени 8:
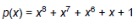 :
:
Раундовое преобразование можно изобразить следующим образом:

Выработка раундовых ключей
Рассмотрим теперь процедуру генерации раундовых ключей из мастер-ключа. Первые два получаются разбиением мастер-ключа пополам. Далее для выработки очередной пары раундовых ключей используется 8 итераций сети Фейстеля, где, в свою очередь, в качестве раундовых ключей используется счетчиковая последовательность, прошедшая через линейное преобразование алгоритма:
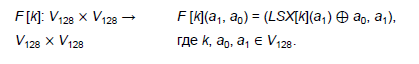

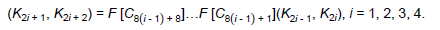
Раунд ключевой развертки можно представить следующим образом:

А всю процедуру выработки раундовых ключей так:

Шифрование и расшифрование
В результате, шифрование одного 128-битного входного блока описывается следующим уравнением:
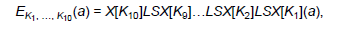
А в виде блок-схемы может быть представлено так:

Расшифрование реализуется обращением базовых преобразований и применением их в обратном порядке:

Ссылки
- Исходное описание стандарта доступно здесь.
- Там же можно загрузить эталонную реализацию.
- Кроме этого своя реализация есть у Маркку-Юхани Сааринена на гитхабе.
