Статьи о получении (псевдо)случайных чисел, о проверке качества полученных последовательностей неизменно вызывают интерес у населения Хабра.
Однако в приложениях наряду с последовательностями случайных и псевдослучайных чисел требуется получать перестановки чисел, имеющие равномерное распределение. Например, потребность в таких перестановках периодически появляется в криптографических приложениях.
Метод описанный ниже предложен Санделиусом (М. Sandelius) еще в 1962 г. в работе [1].
Описываемый алгоритм позволяет получать случайные перестановки из n элементов, которые имеют равномерное распределение. Последнее означает, что вероятность получить одну из n! возможных подстановок, используя данный метод равна 1/n!..
Метод Санделиуса проще описать рекурсивно.
На каждом шаге обрабатывается массив P. Для массива P генерируются случайные биты в количестве равном числу элементов в массиве P. i-тый бит последовательности сопоставляется i-тому элементу массива P. Массив P делится на два массива P0 и P1 по принципу: все элементы, которым сопоставлены нули заносятся в массив P0, остальные в массив P1. Для каждого массива P0 и P1 выполняется перемешивание (рекурсия). Перемешанные массивы объединяются в один. Сначала идут элементы из массива P0, затем из массива P1.
Процедура перемешивания Sandelius(P):
Алгоритм, довольно легко программируется.
Надеюсь, алгоритм генерации перестановки описан мною достаточно понятно. Теперь хочется немного обсудить, особенности его работы.
Для работы алгоритм требует последовательность случайных бит. Главное требование к этой последовательности – биты должны быть независимыми. В этом случае алгоритм генерирует равномерно распределенные перестановки даже.
Следует учитывать, что случайные биты могут иметь неравномерное распределение, но они должны быть независимыми, иначе распределение подстановок не будет равномерным.
К недостаткам можно отнести тот факт, что число случайных бит, которые потребуются для генерации перестановки не определено заранее.
Сразу скажу, что факты указанные в предыдущем пункте доказываются аналитически, но все равно захотелось проверить их на практике.
Для проверки равномерности распределения получаемых подстановок написана простая программа в математическом пакете Maple. В программе я генерировал большое число перестановок, подсчитывал количество подстановок каждого вида (что-то вроде гистограммы). Для полученного массива проверялась гипотеза о равномерности по критерию Пирсона. Кроме того, подсчитывалось распределение количества бит, требуемых для генерации одной подстановки.
Приводить исходный текст программы здесь не вижу смысла, но если есть желание п��считать самим, то файлы с исходными кодами можно найти тут.
Исследовались перестановки длины n=7. Генерировалось N=n!*1000 перестановок. Случайные биты генерировались так: 0 с вероятностью 0,5+d, 1 с вероятностью 0,5-d. d равно 0 для равномерно распределенных бит. Для получения зависимого бита генерировался случайный бит и складывался с предыдущим битом.
Число n=7 взято из соображений разумного времени выполнения (у меня это 10-20 минут).
На рисунках по горизонтали отмечены номера перестановок, а по вертикали частоты их появления. Не вооруженным глазом видно, что в последнем случае распределение сильно отличается от равномерного.
Так же видно, что не зависимо от перекоса в вероятности независимых случайных бит алгоритм генерирует равномерно распределенные перестановки. Однако чем больше перекос в вероятности, тем больше случайных бит требует алгоритм.
Если же биты имеют зависимость, то генерируемые подстановки имеют распределение отличное от равномерного распределения.
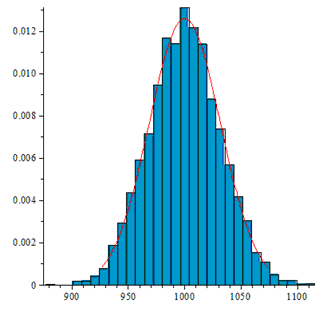
Количество подстановок, каждого типа должно иметь распределение близкое к нормальному со средним N/n! и дисперсией N/n!(1-1/n!).
В первых трех случаях гистограмма выглядит примерно так:
В последнем случае видно, распределение далеко от ожидаемого:
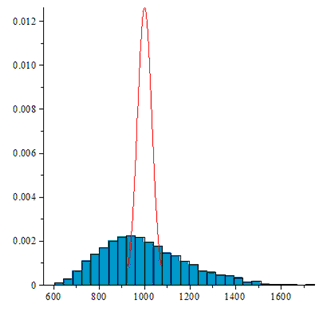
1. М. Sandelius. A Simple Randomisation Procedure, J. of the Royal Statistical Society. Ser. В., V. 24, № 2, 1962.
Однако в приложениях наряду с последовательностями случайных и псевдослучайных чисел требуется получать перестановки чисел, имеющие равномерное распределение. Например, потребность в таких перестановках периодически появляется в криптографических приложениях.
Метод описанный ниже предложен Санделиусом (М. Sandelius) еще в 1962 г. в работе [1].
Описываемый алгоритм позволяет получать случайные перестановки из n элементов, которые имеют равномерное распределение. Последнее означает, что вероятность получить одну из n! возможных подстановок, используя данный метод равна 1/n!..
Алгоритм получения перестановок
Метод Санделиуса проще описать рекурсивно.
На каждом шаге обрабатывается массив P. Для массива P генерируются случайные биты в количестве равном числу элементов в массиве P. i-тый бит последовательности сопоставляется i-тому элементу массива P. Массив P делится на два массива P0 и P1 по принципу: все элементы, которым сопоставлены нули заносятся в массив P0, остальные в массив P1. Для каждого массива P0 и P1 выполняется перемешивание (рекурсия). Перемешанные массивы объединяются в один. Сначала идут элементы из массива P0, затем из массива P1.
Процедура перемешивания Sandelius(P):
1. n := |P|; - мощность (число элементов) P
2. Если n=1, то вернуть P;
3. g:=[gi, i=1..n]; – получение последовательности случайных бит gi
4. P0:=[]; P1:=[]; - пустые массивы
5. i0:=0; i1:=0; - индексы для записи в массивы
6. k:= 0;
7. Если g[k]=0, то
7.1. P0[i0] := P[k];
7.2. i0 := i0+1;
8. Если g[k]=1, то
8.1. P1[i1] := P[k];
8.2. i1 := i1+1;
9. k := k+1;
10. Если k<n, то переходим к шагу 7.
11. P0 := Sandelius(P0);
12. P1 := Sandelius(P1);
13. P := P0||P1 – объединяем массивы в один большой массив.
14. Возвращаем P.
Перестановка по методу Санделиуса получается из последовательности чисел от 1 до n:
P=[1,2, …,n];
Sandelius(P);
Алгоритм, довольно легко программируется.
Вот так, например, можно запрограммировать в Maple
Sandelius:=proc(p)
local A,m,i,p1,p2;
m:=nops(p);
A:=[seq(getNextRndBit(), i=1..m)];
p1:=[]; p2:=[];
for i from 1 to m do
if A[i]=0 then p1:=[op(p1),p[i]];
else p2:=[op(p2),p[i]];
fi;
od;
if nops(p1)>1 then p1:=Sandelius(p1); fi;
if nops(p2)>1 then p2:=Sandelius(p2); fi;
return [op(p1),op(p2)];
end proc:
Вот пример, моей реализации алгоритма на C++, который я использовал в одном своем исследовании
unsigned __int8 *bits,*tmp_perm;
Sandelius(unsigned __int8 *perm,int n)
{
tmp_perm = (unsigned __int8 *)malloc(n);
bits = (unsigned __int8 *)malloc(n);
for(int i=0;i<n;i++) perm[i]=i;
recursiveSandelius(perm,n);
free(bits);
free(tmp_perm);
}
recursiveSandelius(unsigned __int8 *perm,int n)
{
if (n<=1) return;
for(int i=0;i<n;i++)
bits[i]=getNextRndBit();
k=0;
for(int i=0;i<n;i++)
if(!bits[i])
tmp_perm[k++]=perm[i];
zeros=k;
for(int i=0;i<n;i++)
if(bits[i])
tmp_perm[k++]=perm[i];
memcpy(perm,tmp_perm,n);
recursiveSandelius (perm,zeros);
recursiveSandelius (&perm[zeros],n-zeros);
}
Особенности
Надеюсь, алгоритм генерации перестановки описан мною достаточно понятно. Теперь хочется немного обсудить, особенности его работы.
Для работы алгоритм требует последовательность случайных бит. Главное требование к этой последовательности – биты должны быть независимыми. В этом случае алгоритм генерирует равномерно распределенные перестановки даже.
Следует учитывать, что случайные биты могут иметь неравномерное распределение, но они должны быть независимыми, иначе распределение подстановок не будет равномерным.
К недостаткам можно отнести тот факт, что число случайных бит, которые потребуются для генерации перестановки не определено заранее.
Практическая проверка
Сразу скажу, что факты указанные в предыдущем пункте доказываются аналитически, но все равно захотелось проверить их на практике.
Для проверки равномерности распределения получаемых подстановок написана простая программа в математическом пакете Maple. В программе я генерировал большое число перестановок, подсчитывал количество подстановок каждого вида (что-то вроде гистограммы). Для полученного массива проверялась гипотеза о равномерности по критерию Пирсона. Кроме того, подсчитывалось распределение количества бит, требуемых для генерации одной подстановки.
Приводить исходный текст программы здесь не вижу смысла, но если есть желание п��считать самим, то файлы с исходными кодами можно найти тут.
Исследовались перестановки длины n=7. Генерировалось N=n!*1000 перестановок. Случайные биты генерировались так: 0 с вероятностью 0,5+d, 1 с вероятностью 0,5-d. d равно 0 для равномерно распределенных бит. Для получения зависимого бита генерировался случайный бит и складывался с предыдущим битом.
Число n=7 взято из соображений разумного времени выполнения (у меня это 10-20 минут).
| Вариант | Равновероятные подстановки (критерий Пирсона)? | Гистограмма | Среднее число случайных бит/среднеквадратичное отклонение |
|---|---|---|---|
| Независимые биты, d=0 | Да | 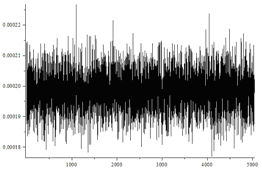 |
28.24/28.26 |
| Независимые биты, d=0.05 | Да | 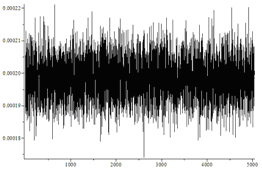 |
28.50/28,54 |
| Независимые биты, d=0.4 | Да |  |
71.47/74.77 |
| Зависимые биты, d=0.05 | Нет |  |
30.15/30.32 |
На рисунках по горизонтали отмечены номера перестановок, а по вертикали частоты их появления. Не вооруженным глазом видно, что в последнем случае распределение сильно отличается от равномерного.
Так же видно, что не зависимо от перекоса в вероятности независимых случайных бит алгоритм генерирует равномерно распределенные перестановки. Однако чем больше перекос в вероятности, тем больше случайных бит требует алгоритм.
Если же биты имеют зависимость, то генерируемые подстановки имеют распределение отличное от равномерного распределения.
Количество подстановок, каждого типа должно иметь распределение близкое к нормальному со средним N/n! и дисперсией N/n!(1-1/n!).
В первых трех случаях гистограмма выглядит примерно так:

В последнем случае видно, распределение далеко от ожидаемого:

Литература
1. М. Sandelius. A Simple Randomisation Procedure, J. of the Royal Statistical Society. Ser. В., V. 24, № 2, 1962.
