
В комментариях проскальзывала мысль, что люди мало комментируют статьи на Habrahabr, т.к. боятся потерять карму. Получается, что в основном пишут те, у кого карма побольше. Попробуем исследовать эту гипотезу подробнее и получить результаты, подкрепленные не только интуитивно, но и статистически.
Нам необходимо проверить, оказывает ли карма пользователя статистически значимое влияние на количество комментариев, которое он в среднем оставляет. Т.к. количество сравниваемых групп будет больше двух, то t-тест не подойдет, и придется использовать дисперсионный анализ — именно так расшифровывается ANOVA (analysis of variance).
Я воспользуюсь данными, которые ранее собрал varagian и выложил тут:
user_data <- read.csv('user_dataset.csv', stringsAsFactors=F, na.strings=c("", "NA"))
Для однофакторного дисперсионного анализа понадобятся две переменные:
- Зависимая переменная, которая в данном случае представляет собой количество комментариев, оставленное пользователем. Ее гистограмма выглядит так:
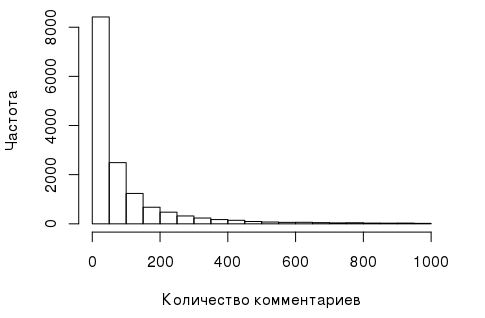
И такое распределение — не самое удачное для дисперсионного анализа, т.к. для его проведения должны выполняться некоторые предпосылки, как, например, нормальность зависимой переменной. К счастью, в данном случае переменную можно «сделать» почти нормальной с помощью ее лог-транформации:
comments_log <- log1p(user_data$comments)

- Факторная переменная, влияние которой на зависимую переменную и исследуется. Посмотрим на распределение кармы:
summary(user_data$karma) Min. 1st Qu. Median Mean 3rd Qu. Max. 0.00 0.00 5.00 17.92 18.00 1230.00
Чтобы сгруппировать данные, введем новую переменную, которая будет представлять собой интервальный «срез» кармы и играть роль факторной переменной:
karma_cut <- cut(user_data$karma, breaks=c(-Inf, 0, 5, 15, 25, 50, 100, Inf)) table(karma_cut) (-Inf,0] (0,5] (5,15] (15,25] (25,50] (50,100] (100, Inf] 5488 2059 2955 1423 1411 859 480
Самая многочисленная группа — это пользователи с кармой меньше или равной 0.
Nota bene!
Тут я должен сказать несколько слов о преобразовании непрерывной переменной в категориальную. Такая практика широко распространена в социологических, психологических и медико-биологических исследованиях: например, величину артериального давления можно условно определить как пониженное, нормальное, высокое. Но в целом с точки зрения статистики эта процедура несколько порочна, т.к. любое разбиение весьма условно, что потенциально ведет к потере информации.
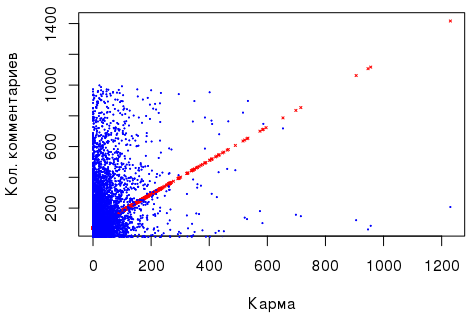
Что же касается зависимости «количество комментариев» ~ «карма», то тут есть небольшая положительная корреляция, а линейная регрессия, выполненная на основе этих двух численных показателей (см. выше), являясь значимой, выглядит неубедительно, чтобы на ее основе делать какие-то статистические выводы: например, RESET-тест Рамсея сигнализирует о пропущенных переменных, а тест Бройша-Пагана — о гетероскедастичности случайных ошибок. Кроме того, я заранее ставлю задачу сравнить группы пользователей, у которых карма воспринимается как «маленькая», «средняя» и.т.д.

Что же касается зависимости «количество комментариев» ~ «карма», то тут есть небольшая положительная корреляция, а линейная регрессия, выполненная на основе этих двух численных показателей (см. выше), являясь значимой, выглядит неубедительно, чтобы на ее основе делать какие-то статистические выводы: например, RESET-тест Рамсея сигнализирует о пропущенных переменных, а тест Бройша-Пагана — о гетероскедастичности случайных ошибок. Кроме того, я заранее ставлю задачу сравнить группы пользователей, у которых карма воспринимается как «маленькая», «средняя» и.т.д.
Вот как распределяются медианы в зависимости от интервала, в который попадает карма пользователя:
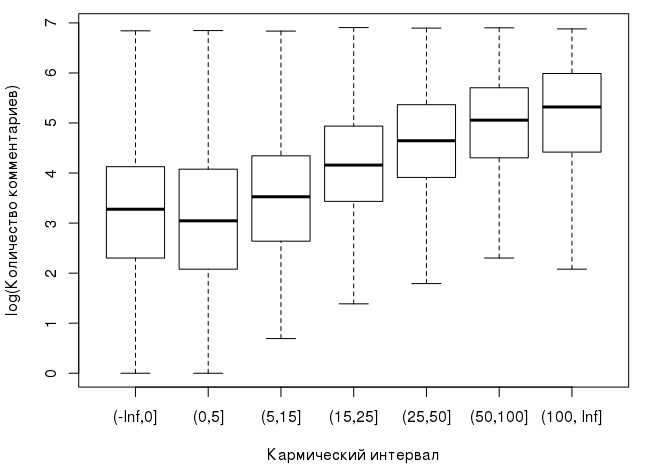
Уже можно наблюдать, что с ростом кармы растет и медиана количества комментариев, которое оставляет пользователь. С учетом сказанного нашу нулевую гипотезу для дисперсионного анализа можно сформулировать так: карма не оказывает никакого влияния на логарифм количества оставляемых пользователем комментариев, а наблюдаемые различия между групповыми средними несущественны и случайны:

Альтернативная гипотеза, соответственно, утверждает, что различия все же не случайны. Чтобы принять или отклонить нуле��ую гипотезу, нам надо сравнить межгрупповую VARb и внутригрупповую VARw дисперсии. Обе эти величины по-своему оценивают дисперсию генеральной совокупности, и при верной нулевой гипотезе их отношение находится недалеко от 1, т.е. внутригрупповая и межгрупповая дисперсии не различаются. Формулы для вычисления этих дисперсий приведены ниже:

Тут K — количество групп, N — общий объем выборки. Теперь надо оценить соотношение

В этом контексте принято говорить, что величина F следует F-распределению со степенями свободы K-1 и N-K. Небольшой фрагмент кода на R, который вычисляет статистику Ftest и критическое значение Fcrit при уровне значимости α=5%:
alpha <- 0.05 K <- length(levels(karma_cut)) N <- nrow(user_data) df1 <- K - 1 df2 <- N - K M <- mean(comments_log) var_b <- sum(tapply(comments_log, karma_cut, function(x){ length(x) * (mean(x) - M) ^ 2})) / df1 var_w <- sum(tapply(comments_log,karma_cut, function(x){ sum((x - mean(x))^2)})) / df2 Ftest <- var_b / var_w Fcrit <- qf(alpha, df1, df2, lower.tail=F)
Ниже на графике показано распределение F(6, 14668), критическое и вычисленное значения статистик:

Очевидно, что Fcrit<<Ftest, а значит, гипотезу H0 можно отвергнуть. В R, конечно, все вышеописанное уже давно реализовано, поэтому просто проверим вычисления:
m.aov <- aov(comments_log ~ karma_cut) summary(m.aov) Df Sum Sq Mean Sq F value Pr(>F) karma_cut 6 5519 919.9 556.2 <2e-16 *** Residuals 14668 24260 1.7 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Значение F-статистики 556.2, что совпадает с вычисленным ранее.
Post hoc
Расчеты показывают, что гипотеза H0 о равенстве средних должна быть отклонена (это единственное, что мы можем сказать, выполнив ANOVA). Что делать с этим выводом дальше? Обычно после ANOVA выполняют post hoc анализ: можно применить t-тест с поправкой Бонферрони (в R это pairwise.t.test) или, например, HSD тест Тьюки, чтобы выяснить, между какими группами существуют различия. Последний тест мне больше нравится:
TukeyHSD(m.aov, "karma_cut", conf.level=0.95) Tukey multiple comparisons of means 95% family-wise confidence level Fit: aov(formula = comments_log ~ karma_cut) $karma_cut diff lwr upr p adj (0,5]-(-Inf,0] -0.08189943 -0.17990408 0.01610521 0.1725558 (5,15]-(-Inf,0] 0.29578008 0.20925195 0.38230821 0.0000000 (15,25]-(-Inf,0] 0.92766799 0.81485590 1.04048009 0.0000000 (25,50]-(-Inf,0] 1.36762030 1.25442791 1.48081269 0.0000000 (50,100]-(-Inf,0] 1.66955943 1.53041195 1.80870691 0.0000000 (100, Inf]-(-Inf,0] 1.87283311 1.69233134 2.05333488 0.0000000 (5,15]-(0,5] 0.37767952 0.26881660 0.48654243 0.0000000 (15,25]-(0,5] 1.00956743 0.87883646 1.14029840 0.0000000 (25,50]-(0,5] 1.44951973 1.31846045 1.58057902 0.0000000 (50,100]-(0,5] 1.75145887 1.59742628 1.90549145 0.0000000 (100, Inf]-(0,5] 1.95473255 1.76252197 2.14694313 0.0000000 (15,25]-(5,15] 0.63188791 0.50952455 0.75425128 0.0000000 (25,50]-(5,15] 1.07184022 0.94912615 1.19455428 0.0000000 (50,100]-(5,15] 1.37377935 1.22678192 1.52077678 0.0000000 (100, Inf]-(5,15] 1.57705303 1.39043280 1.76367327 0.0000000 (25,50]-(15,25] 0.43995231 0.29748058 0.58242403 0.0000000 (50,100]-(15,25] 0.74189144 0.57803877 0.90574410 0.0000000 (100, Inf]-(15,25] 0.94516512 0.74499878 1.14533146 0.0000000 (50,100]-(25,50] 0.30193913 0.13782440 0.46605386 0.0000012 (100, Inf]-(25,50] 0.50521281 0.30483189 0.70559373 0.0000000 (100, Inf]-(50,100] 0.20327368 -0.01283281 0.41938017 0.0811265
Предварительно можно сделать вывод, что пользователи с кармой (-∞, 0] и (0, 5] оставляют примерно одинаковое log-количество комментариев, как и пользователи с кармой (50,100] и (100, ∞]. Остальные группы существенно отличаются.
Что не так?
На этом можно было бы и остановиться, но есть несколько замечаний вдобавок к тому, что находится под спойлером выше. Прежде всего, стоит обратить внимание на нашу «нормализованную» переменную comments_log:
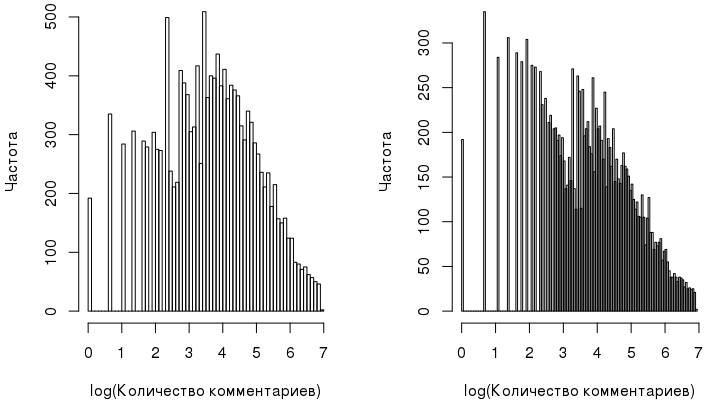
При более детальном рассмотрении она оказывается весьма далекой от нормального распределения, на что намекает и тест Шапиро-Уилка. Другой критерий — тест Бартлетта — свидетельствует о том, что дисперсия в группах неоднородна:
bartlett.test(comments_log~karma_cut) Bartlett test of homogeneity of variances data: comments_log by karma_cut Bartlett's K-squared = 84.811, df = 6, p-value = 3.613e-16
С одной стороны — нарушение предпосылок ANOVA налицо, с другой — есть ряд работ, которые говорят, что дисперсионный анализ весьма устойчив и к нарушению условия нормальности, и к неоднородности дисперсии. Если нарушение условий все же кого-то стесняют, то можно воспользоваться непараметрическим тестом Краскела-Уоллиса. Тут в качестве нулевой гипотезы выступает предположение о равенстве м��диан (а не средних!) во всех группах:
kruskal.test(comments_log ~ karma_cut) Kruskal-Wallis rank sum test data: comments_log by karma_cut Kruskal-Wallis chi-squared = 2816.1, df = 6, p-value < 2.2e-16
Тест Краскела-Уоллиса также позволяет отклонить нулевую гипотезу. Т.к. критерий Краскела-Уоллиса непараметрический, то и post-hoc анализ тоже должен основываться на непараметрических тестах, как, например, U-критерий Манна-Уитни с последующей коррекцией p-значений, тест Данна. Последний содержится в пакете R dunn.test:
dunn.test::dunn.test(comments_log, karma_cut, method="bonferroni")

При 5% уровне значимости, как и тест Тьюки, критерий Данна говорит о том, что пользователи с кармой (-∞, 0] и (0, 5], и (50,100] и (100, ∞]. оставляют примерно одинаковое log-количество комментариев.
ANOVA и линейная регрессия
Говоря о дисперсионном анализе, нельзя не упомянуть о линейной регрессии. Более того, можно утверждать, что это практически одно и то же, т.к. модель дисперсионного анализа — частный случай линейной регрессии. Запишем линейную регрессию с факторной переменной и проверим ее коэффициенты:
m.lm <- lm(comments_log ~ karma_cut-1) summary(m.lm) Coefficients: Estimate Std. Error t value Pr(>|t|) karma_cut(-Inf,0] 3.20288 0.01736 184.50 <2e-16 *** karma_cut(0,5] 3.12098 0.02834 110.12 <2e-16 *** karma_cut(5,15] 3.49866 0.02366 147.88 <2e-16 *** karma_cut(15,25] 4.13055 0.03409 121.16 <2e-16 *** karma_cut(25,50] 4.57050 0.03424 133.50 <2e-16 *** karma_cut(50,100] 4.87244 0.04388 111.04 <2e-16 *** karma_cut(100, Inf] 5.07571 0.05870 86.47 <2e-16 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 1.286 on 14668 degrees of freedom Multiple R-squared: 0.8914, Adjusted R-squared: 0.8913 F-statistic: 1.719e+04 on 7 and 14668 DF, p-value: < 2.2e-16
Теперь найдем среднее количество лог-комментариев по каждому кармическому срезу:
tapply(comments_log, karma_cut, mean) (-Inf,0] (0,5] (5,15] (15,25] (25,50] (50,100] (100, Inf] 3.202879 3.120979 3.498659 4.130547 4.570499 4.872438 5.075712
Коэффициенты в линейной регрессии — это и есть средние значения, т.е. справедлива такая формула:

где μi — среднее соответствующей группы, εij — случайная ошибка, распределенная нормально.
Заключение
Итак, анализ дисперсии выполняется по такой схеме:
- Определяются зависимая и факторная переменная.
- Проверяются предпосылки для проведения ANOVA.
- При нормальной зависимой переменной и однородной дисперсии выполняется ANOVA, иначе — непараметрический тест Краскела-Уоллиса
- После анализа дисперсии и отвергания нулевой гипотезы, выполняется соответствующий рost-hoc анализ — параметрический или непараметрический.
При многофакторном анализе дисперсий так же применяется F-тест, но формулы для расчета дисперсии усложняются; кроме того, возникают дополнительные термы, описывающие взаимодействие между факторами, и появляется несколько нулевых гипотез.
Что касается комментариев на Хабре, то и ANOVA, и тест Краскела-Уоллиса говорят, что есть зависимость между log-количеством комментариев и кармой пользователя, причем группы с кармой (-∞, 0] и (0, 5], и (50,100] и (100, ∞] оставляют примерно одинаковое количество комментариев. В целом, с ростом самой кармы увеличивается и количество комментариев. Интересно, что результаты и непараметрического, и параметрического тестов совпали, хотя предпосылки для проведения последнего были явно нарушены. Объяснить этот факт можно как робастностью дисперсионного анализа, так и тем, что при большом количестве данных (у нас есть тысячи измерений) нарушение предположения о нормальности данных оказывает гораздо меньшее влияние на результат, чем в случае с малой выборкой.
