Зачастую, во время работы с нейронными сетями, перед нами встает задача в построении линейных решающих функций (ЛРФ) для разделения классов, содержащих наши образы.

Рисунок 1. двумерный случай
Один из методов, позволяющих решить нашу проблему, это алгоритм наименьшей среднеквадратичной ошибки (НСКО алгоритм).
Интерес данный алгоритм представляет не только в том, что он помогает построить необходимые нам ЛРФ, а в том, что при возникновении ситуации, когда классы линейно неразделимы, мы можем построить ЛРФ, где ошибка неправильной классификации стремится к минимуму.

Рисунок 2. линейно неразделимые классы
Далее перечислим исходные данные:
 — обозначение класса (i — номер класса)
— обозначение класса (i — номер класса)
 — обучающая выборка
— обучающая выборка
 — метки( номер класса к которому относится образ
— метки( номер класса к которому относится образ 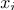 )
)
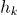 — скорость обучения (произвольная величина)
— скорость обучения (произвольная величина)
Этой информации нам более чем достаточно для построения ЛРФ.
Перейдем непосредственно к самому алгоритму.
а) переводим в систему
в систему  , где
, где  равен
равен  , у которого в конце приписан класс образа
, у которого в конце приписан класс образа
Например:
Пусть задан образ .
.
Тогда
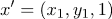 , если
, если  из 1 класса
из 1 класса
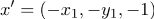 , если
, если  из 2 класса
из 2 класса
б) строим матрицу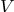 размерностью Nx3 которая состоит из наших векторов
размерностью Nx3 которая состоит из наших векторов 
в) ст��оим
г) считаем где
где  произвольный вектор(по умолчанию единичный)
произвольный вектор(по умолчанию единичный)
д) (номер итерации)
(номер итерации)
Проверяем условие останова:
Если то «СТОП»
то «СТОП»
иначе — переходим к шагу 3
а)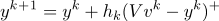 (где + это функция Хэвисайда)
(где + это функция Хэвисайда)
Например(функция Хэвисайда):

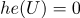 (если
(если  )
)
 (если
(если  или
или  )
)
После подсчетов меняем номер итерации:

б) переходим на шаг 2

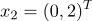
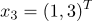
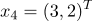
 принадлежат 1 классу
принадлежат 1 классу 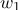
 принадлежат 2 классу
принадлежат 2 классу 
а)

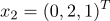
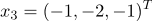

б)
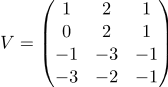
в)

г)


д)
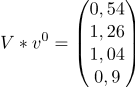 , т.к. все элементы
, т.к. все элементы 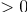
 «СТОП»
«СТОП»
Завершили работу алгоритма, и теперь можно подсчитать нашу ЛРФ.

Спасибо parpalak за онлайн редактор.
Спасибо за внимание.

Рисунок 1. двумерный случай
Один из методов, позволяющих решить нашу проблему, это алгоритм наименьшей среднеквадратичной ошибки (НСКО алгоритм).
Интерес данный алгоритм представляет не только в том, что он помогает построить необходимые нам ЛРФ, а в том, что при возникновении ситуации, когда классы линейно неразделимы, мы можем построить ЛРФ, где ошибка неправильной классификации стремится к минимуму.

Рисунок 2. линейно неразделимые классы
Далее перечислим исходные данные:
 — обозначение класса (i — номер класса)
— обозначение класса (i — номер класса) — обучающая выборка
— обучающая выборка — метки( номер класса к которому относится образ
— метки( номер класса к которому относится образ 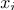 )
)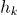 — скорость обучения (произвольная величина)
— скорость обучения (произвольная величина)Этой информации нам более чем достаточно для построения ЛРФ.
Перейдем непосредственно к самому алгоритму.
Алгоритм
1 шаг
а) переводим
 в систему
в систему  , где
, где  равен
равен  , у которого в конце приписан класс образа
, у которого в конце приписан класс образаНапример:
Пусть задан образ
 .
.Тогда
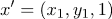 , если
, если  из 1 класса
из 1 класса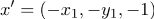 , если
, если  из 2 класса
из 2 классаб) строим матрицу
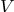 размерностью Nx3 которая состоит из наших векторов
размерностью Nx3 которая состоит из наших векторов 
в) ст��оим

г) считаем
 где
где  произвольный вектор(по умолчанию единичный)
произвольный вектор(по умолчанию единичный)д)
 (номер итерации)
(номер итерации)2 шаг
Проверяем условие останова:
Если
 то «СТОП»
то «СТОП»иначе — переходим к шагу 3
3 шаг
а)
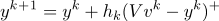 (где + это функция Хэвисайда)
(где + это функция Хэвисайда)Например(функция Хэвисайда):

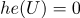 (если
(если  )
) (если
(если  или
или  )
)После подсчетов меняем номер итерации:

б) переходим на шаг 2
Пример работы алгоритма НСКО

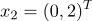
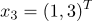
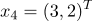
 принадлежат 1 классу
принадлежат 1 классу 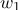
 принадлежат 2 классу
принадлежат 2 классу 
а)

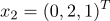
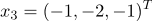

б)
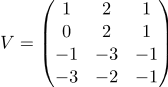
в)

г)


д)

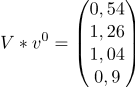 , т.к. все элементы
, т.к. все элементы 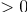
 «СТОП»
«СТОП»Завершили работу алгоритма, и теперь можно подсчитать нашу ЛРФ.

Спасибо parpalak за онлайн редактор.
Спасибо за внимание.
