gridem 6 апр 2017 в 12:40

Кинетика больших кластеров

10 мин

5.4K

Алгоритмы*Анализ и проектирование систем*Высокая производительность*Промышленное программирование*Распределённые системы*

Краткое содержание

Фатальная ошибка Мартина Клеппмана.
Физико-химическая кинетика уделывает математику.
Период полураспада кластера.
Решаем нелинейные дифференциальные уравнения, не решая их.
Ноды как катализатор.
Предсказательная сила графиков.
100 миллионов лет.
Синергия.

В предыдущей заметке мы подробно разбирали статью Брюера и его одноименную теорему. На этот раз займемся препарированием поста Мартина Клеппмана «The probability of data loss in large clusters».

В данном посте автор пытается промоделировать следующую задачу. Для обеспечения сохранности данных обычно используется метод репликации данных. При этом, на самом деле, не важно, используется ли erasure кодирование или нет. В оригинальном посте автор задает вероятность выпадения одной ноды, а затем ставит вопрос: а какова вероятность выпадения данных при увеличении числа нод?

Ответ приведен на этой картинке:

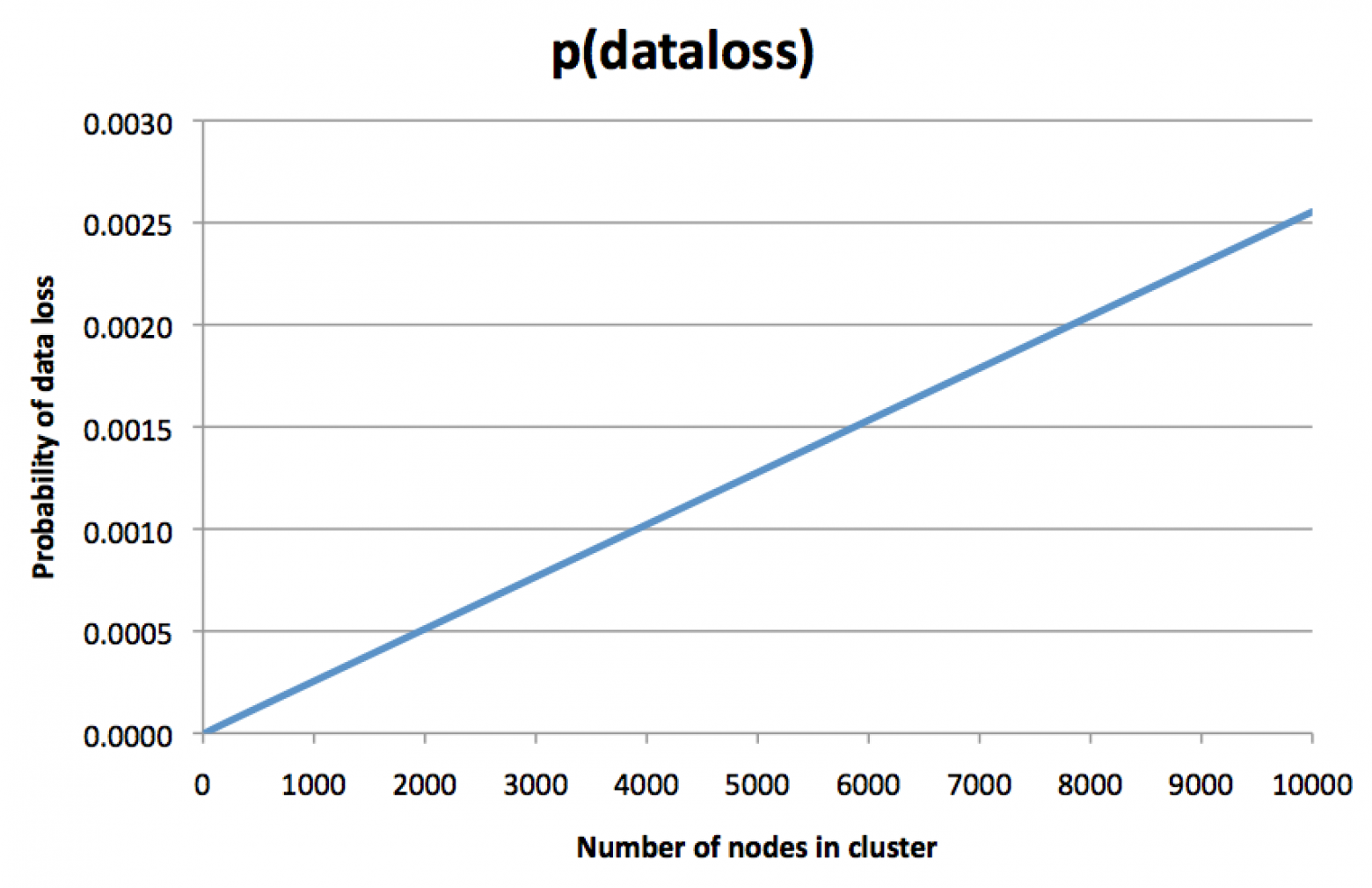
Data loss

Т.е. с ростом числа нод число потерянных данных растет прямопропорционально.

Почему это важно? Если мы рассмотрим размеры современных кластеров, то увидим, что их число с течением времени непрерывно растет. А значит возникает резонный вопрос: стоит ли беспокоиться за сохранность своих данных и поднимать фактор репликации? Ведь это напрямую влияет на бизнес, стоимость владения и проч. Также на этом примере можно замечательно продемонстрировать, как можно выдать математически корректный, но неправильный результат.

Моделирование кластера

Для демонстрации ошибочности расчетов полезно понимать, что такое модель и моделирование. Если модель плохо описывает реальное поведение системы, то какие бы правильные формулы не использовались, мы можем легко получить неправильный результат. А все из-за того, что наша модель может не учитывать какие-то важные параметры системы, которыми нельзя пренебрегать. Искусство состоит в том, чтобы понять, что важно, а что нет.

Для описания жизнедеятельности кластера важно учитывать динамику изменений и взаимосвязь различных процессов. Это как раз и является слабым звеном оригинальной статьи, т.к. там бралась статическая картинка без каких-либо особенностей, связанных с репликацией.

Для описания динамики я буду использовать методы химической кинетики, где я вместо ансамбля частиц буду использовать ансамбль нод. Насколько я знаю, никто не использовал такой формализм для описания поведения кластеров. Поэтому буду импровизировать.

Введем следующие обозначения:

: общее число нод кластера
: число работоспособных нод (available)
: число проблемных нод (failed)

Тогда очевидно, что:

$\begin{aligned} N = A + F \\ \end{aligned}$

В число проблемных нод я буду включать любые проблемы: диск навернулся, сломался процессор, сеть и т.п. Мне не важна причина, важен сам факт поломки и недоступности данных. В дальнейшем, конечно же, можно учитывать более тонкую динамику.

Теперь запишем кинетические уравнения процессов поломки и восстановления нод кластера:

$\begin{aligned} A & \xrightarrow{k_f} F &(1) \\ F & \xrightarrow{k_a} A &(2) \\ \end{aligned}$

Эти простейшие уравнения говорят следующее. Первое уравнение описывает процесс поломки ноды. Оно не зависит от каких-либо параметров и описывает изолированный выход ноды из строя. Другие ноды в этом процессе не участвуют. Слева используется исходный «состав» участников процесса, а справа — продукты процесса. Константы скорости k_f

задают скоростные характеристики процессов для поломки и восстановления нод соответственно.

Выясним физический смысл констант скоростей. Для этого запишем кинетические уравнения:

$\begin{aligned} \frac{dA}{dt} &= -k_f A + k_a F \\ \frac{dF}{dt} &= k_f A - k_a F \\ \end{aligned}$

Из этих уравнений понятен смысл констант k_f

. Если предположить, что админов нет и кластер сам себя не исцеляет (т.е. k_a = 0

), то сразу получаем уравнение:

$\begin{aligned} \frac{dA}{dt} = -k_f A \\ \end{aligned}$

Или

$\begin{aligned} A = N e^{-k_f t} \\ \end{aligned}$

Т.е. величина 1/k_f

— это период полураспада кластера на запчасти, с точностью до e/2

. Пусть $\tau_f$ — характерное время перехода единичной ноды из состояния

в состояние

, а $\tau_a$ — характерное время перехода единичной ноды из состояния

в состояние

. Тогда

$\begin{aligned} \tau_f &\sim \frac{1}{k_f} \\ \tau_a &\sim \frac{1}{k_a} \\ \frac{\tau_a}{\tau_f} &= \frac{k_f}{k_a} \\ \end{aligned}$

Решим наши кинетические уравнения. Сразу хочу оговориться, что я буду срезать углы везде, где это только можно, чтобы получить максимально простые аналитические зависимости, которые буду использовать для возможных предсказаний и тюнинга.

Т.к. максимальный лимит на количество решений дифференциальных уравнений достигнут, то буду решать эти уравнения методом квазистационарных состояний:

$\begin{aligned} \frac{dA}{dt} = 0 \Rightarrow F = A \frac{k_f}{k_a} \\ \end{aligned}$

С учетом того, что $F \ll N$ (это вполне разумное предположение, в противном случае надо покупать более качественное железо или более продвинутых админов), получаем:

$\begin{aligned} A &\simeq N \\ F &= N \frac{k_f}{k_a} \\ \end{aligned}$

Если положить, что время восстановления $\tau_a$ примерно 1 неделя, а время смерти $\tau_f$ примерно 1 год, получаем, что доля сломанных нод p_f

$\begin{aligned} p_f = \frac{F}{N} = \frac{\tau_a}{\tau_f} \approx 2\% \\ \end{aligned}$

Чанки

Обозначим через

— количество недореплицированных (underreplicated) чанков, которые необходимо дореплицировать после выпадения ноды при переходе в состояние

. Тогда для учета чанков, поправим наши уравнения:

$\begin{aligned} A & \xrightarrow{k_f} F + U &(1) \\ F & \xrightarrow{k_a} A &(2) \\ U + A & \xrightarrow{k_r} H + A &(3) \\ \end{aligned}$

где

— константа скорости репликации процесса второго порядка, а

означает здоровый (healthy) чанк, который растворится в общей массе чанков.

3-е уравнение необходимо пояснить. Оно описывает процесс второго порядка, а не первого:

$\begin{aligned} U & \xrightarrow{k_r} H \\ \end{aligned}$

Если бы мы так сделали, то получили бы кривую Клеппмана, что не входит в мои планы. На самом деле в процессе восстановления участвуют все ноды, и чем больше нод, тем быстрее идет процесс. Связано это с тем, что чанки с убитой ноды распределяются примерно равномерно по всему кластеру, поэтому каждому участнику необходимо отреплицировать в

раз меньше. Это означает, что итоговая скорость восстановления чанков с убитой ноды будет пропорциональна количеству доступных нод.

Стоит также отметить, что в уравнении (3) слева и справа стоит

, и при этом он не расходуется. Химики бы сразу заявили, что в данному случае

выступает в роли катализатора. И если внимательно подумать, то так оно и есть на самом деле.

Применяя метод квазистационарных концентраций мгновенно получаем результат:

$\begin{aligned} \frac{dU}{dt} = 0 = k_f A - k_r U A \\ \end{aligned}$

или

$\begin{aligned} U = \frac{k_f}{k_r} \\ \end{aligned}$

Удивительный результат! Т.е. количество чанков, которые необходимо отреплицировать, не зависит от количества нод! А связано это как раз с тем, что увеличение числа нод увеличивает результирующую скорость реакции (3), тем самым компенсируя большее количество

нод. Катализ!

Оценим это значение. $\tau_r$ — время восстановления чанков, как если бы у нас была только одна нода. Пусть на ноде надо отреплицировать 5ТБ данных, при этом поток репликации в байтах зададим как 50МБ/с, тогда получим:

$\begin{aligned} U = \frac{\tau_r}{\tau_f} \approx \frac{1 \times 10^5}{3.2 \times 10^7} \approx 3 \times 10^{-3} \\ \end{aligned}$

Т.е. $U \ll 1$ и можно не бояться за сохранность данных. Тут стоит учесть, что потеря одного чанка из 3-х не приводит к потере данных.

Планирование репликации

В предыдущем расчете мы сделали неявное предположение о том, что ноды мгновенно узнают о том, какие конкретно чанки необходимо отреплицировать, и сразу же начинают процесс их репликации. В реальности это совершенно не так: мастеру необходимо понять, что нода умерла, затем понять какие конкретно чанки необходимо отреплицировать и запустить процесс репликации на нодах. Все это не мгновенно и занимает какое-то время $\tau_s$ (scheduling).

Для учета запаздывания воспользуемся теорией переходного состояния или активированного комплекса, которая описывает процесс перехода через седловую точку на многомерной поверхности потенциальной энергии. С нашей точки зрения у нас будет некоторое дополнительное промежуточное состояние U^*

, которое означает, что этот чанк запланировали на репликацию, но процесс репликации еще не начат. Т.е. в следующую наносекунду репликация точно начнется, но не пикосекундой раньше. Тогда наша система примет окончательный вид:

$\begin{aligned} A & \xrightarrow{k_f} F + U &(1) \\ F & \xrightarrow{k_a} A &(2) \\ U & \xrightarrow{k_s} U^* &(3) \\ U^* + A & \xrightarrow{k_r} H + A &(4) \\ \end{aligned}$

Решая его, находим, что:

$\begin{aligned} \frac{dU}{dt} &= k_f A - k_s U \\ \frac{dU^*}{dt} &= k_s U - k_r U^* A \\ \end{aligned}$

Применяя метод квазистационарных концентраций, находим:

$\begin{aligned} U &= A \frac{k_f}{k_s} \\ U^* &= \frac{k_f}{k_r} \\ U_{sum} &= U + U^* = \frac{\tau_r}{\tau_f} \bigg( 1 + \frac{A}{\widetilde{A}} \bigg) \\ \end{aligned}$

где:

$\begin{aligned} \widetilde{A} = \frac{\tau_r}{\tau_s} \\ \end{aligned}$

Как видим, результат совпадает с предыдущим за исключением множителя $(1+A/\widetilde{A})$ . Рассмотрим 2 предельных случая:

$A \ll \widetilde{A}$ . В этом случае все рассуждения, приведенные ранее, сохраняются: количество чанков не зависит от числа нод, а значит не растет с ростом кластера.
$A \gg \widetilde{A}$ . В этом случае $U_{sum} \simeq A \tau_s / \tau_f$ и растет линейно с ростом числа нод.

Для определения режима оценим, чему равна $\widetilde{A}$ . $\tau_s$ — это характерное суммарное время обнаружения недореплицированного чанка и планирование его репликации. Грубая оценка (используя методику «пальцем в небо») дает значение 100 с. Тогда:

$\begin{aligned} \widetilde{A} = \frac{1 \times 10^5}{100} = 1000 \\ \end{aligned}$

Таким образом дальнейшее увеличение кластера сверх этой цифры при данных условиях начнет повышать вероятность потери чанка.

Что можно сделать для улучшения ситуации? Казалось бы, можно улучшить асимптотику сдвинув границу $\widetilde{A}$ путем увеличения $\tau_r$ , однако это лишь увеличит значение $U_{sum}$ без какого-либо реального улучшения. Самый верный способ: это уменьшение $\tau_s$ , т.е. время принятия решения для репликации чанка, т.к. $\tau_f$ зависит от характеристик железа и на это программными средствами повлиять тяжело.

Обсуждение предельных случаев

Предлагаемая модель фактически разбивает совокупность кластеров на 2 лагеря.

К первому лагерю примыкают сравнительно небольшие кластера с количеством нод < 1000. В этом случае вероятность получить недореплицированный чанк описывается простой формулой:

$\begin{aligned} U = \frac{\tau_r}{\tau_f} \\ \end{aligned}$

Для улучшения ситуации можно применять 2 подхода:

Улучшать железо, тем самым увеличивая $\tau_f$ .
Ускорять репликацию, уменьшая $\tau_r$ .

Эти способы в целом являются достаточно очевидными.

Во втором лагере мы имеем уже крупные и сверхкрупные сервера с числом нод > 1000. Здесь зависимость будет определяться следующим образом:

$\begin{aligned} U = A \frac{\tau_s}{\tau_f} \\ \end{aligned}$

Т.е. будет прямопропорционально числу нод, а значит последующее увеличение кластера будет негативно сказываться на вероятности появления недореплицированных чанков. Однако и здесь можно существенно снизить негативные эффекты, используя следующие подходы:

Продолжать увеличивать $\tau_f$ .
Ускорять детектирование недореплицированных чанков и последующее планирование репликации, тем самым уменьшая $\tau_s$ .

2-й подход по уменьшению $\tau_s$ уже не является очевидным. Казалось бы, какая разница, пройдет 20 секунд или 100 секунд? Однако эта величина существенно влияет на вероятность появления недореплицированных чанков. Также неочевидным является тот факт, что пропадает зависимость от $\tau_r$ , т.е. сама скорость репликации не играет роли. Оно и понятно в этой модели: с ростом числа нод эта скорость только увеличивается, поэтому на репликацию чанка начинает существенно влиять константная добавка «разгона» процесса репликации, направленная на обнаружение и планирование репликации.

Стоит остановиться немножко подробнее на $\tau_f$ . Помимо непосредственного вклада в жизнедеятельность чанков, увеличение $\tau_f$ благотворно сказывается на количестве доступных нод, т.к.

$\begin{aligned} A = N - F \simeq N \bigg( 1 - \frac{\tau_a}{\tau_f} \bigg) \\ \end{aligned}$

Тем самым увеличивая число доступных нод. Таким образом, улучшение $\tau_f$ напрямую сказывается на наличие доступных ресурсов кластера, ускоряя вычисления и одновременно повышая надежность хранения данных. С другой стороны, улучшение качества железа напрямую влияет на стоимость владения кластера. Описанная модель позволяет количественно оценивать экономическую целесообразность такого рода решений.

Сравнение подходов

В заключении я хотел бы привести сравнение двух подходов. Про это красноречиво скажут следующие графики.

Data loss

Из первого графика можно только увидеть линейную зависимость, однако она не даст ответа на вопрос: «а что нужно сделать, чтобы улучшить ситуацию?» Вторая же картинка описывает более сложную модель, которая сразу может дать ответы на вопросы о том, что делать и как повлиять на поведение процесса репликации. Более того, она дает рецепт быстрого способа, буквально в уме, оценивания последствий тех или иных архитектурных решений. Иначе говоря, предсказательная сила развитой модели находится на качественно ином уровне.

Потеря чанка

Найдем теперь характерное время потери чанка. Для этого выпишем кинетику процессов образования таких чанков с учетом степени репликации = 3:

$\begin{aligned} A & \xrightarrow{k_f} F + U \\ F & \xrightarrow{k_a} A \\ U & \xrightarrow{k_s} U^* \\ U^* + A & \xrightarrow{k_r} H + A \\ U & \xrightarrow{k_f} F + U_2 \\ U^* & \xrightarrow{k_f} F + U_2 \\ U_2 & \xrightarrow{k_s} U_2^* \\ U_2^* + A & \xrightarrow{k_r} U + A \\ U_2 & \xrightarrow{k_f} F + L \\ U_2^* & \xrightarrow{k_f} F + L \\ \end{aligned}$

Здесь через U_2

обозначено количество недореплицированных чанков, которым не хватает двух копий, U_2^*

— промежуточное состояние, аналогично U^*

, соответствующее состоянию U_2

, а

означает потерянный (lost) чанк. Тогда:

$\begin{aligned} \frac{dL}{dt} &= k_f \big( U_2 + U_2^* \big) \\ \tau_l &= \frac{1}{k_f \big( U_2 + U_2^* \big) } \\ \end{aligned}$

Где $\tau_l$ — характерное время образования потерянного чанка. Решим нашу систему для 2-х предельных случаев для случая, когда A = 1000

.

$A \ll \widetilde{A}$ , тогда

$\begin{aligned} \tau_l = A \frac{\tau_f^3}{\tau_r^2} \approx 100\ 000\ 000\ years \\ \end{aligned}$

Для $A \gg \widetilde{A}$ получаем:

$\begin{aligned} \tau_l = \frac{\tau_f^3}{A \tau_s^2} \approx 100\ 000\ 000\ years \\ \end{aligned}$

Т.е. характерное время образования потерянного чанка 100 миллионов лет! При этом получаются примерно сходные значения, т.к. мы находимся в переходной зоне. Величина характерного времени $\tau_l$ говорит сама за себя и каждый может сделать выводы сам.

Стоит, однако, обратить внимание на одну особенность. В предельном случае $A \ll \widetilde{A}$ в то время, как

является константой и не зависит от

, в выражении для $\tau_l$ мы получаем обратную зависимость, т.е. с ростом кластера тройная репликация даже улучшает сохранность данных! С дальнейшим ростом кластера ситуация меняется ровно на противоположную.

Выводы

Статья последовательно вводит инновационный способ моделирования кинетики процессов больших кластеров. Рассмотренная приближенная модель описания динамики кластера позволяет посчитать вероятностные характеристики, описывающие потерю данных.

Конечно, данная модель является лишь первым приближением к тому, что реально происходит на кластере. Здесь мы лишь учитывали наиболее значимые процессы для получения качественного результата. Но даже такая модель позволяет судить о том, что происходит внутри кластера, а также дает рекомендации для улучшения ситуации.

Тем не менее, предложенный подход позволяет более точные и достоверные результаты, основанные на тонком учете различных факторов и анализе реальных данных работы кластера. Ниже приведен далеко не исчерпывающий список по улучшению модели:

Ноды кластера могут выходить из строя из-за различных сбоев оборудования. Поломка конкретного узла как правило имеет различную вероятность. Более того, поломка, например, процессора, не теряет данные, а лишь дает временную недоступность ноды. Это легко учитывать в модели, вводя различные состояния $F_{proc}$ , $F_{disk}$ , $F_{mem}$ и т.д. с различными скоростями процессов и различными последствиями.
Не все ноды одинаково полезны. Разные партии могут отличаться разным характером и частотой сбоев. Это такое можно учитывать в модели, вводя , и т.п. с разными скоростями соответствующих процессов.
Добавление в модель нод различных типов: с частично поврежденными дисками, забаненные и др. Например, можно детально проанализировать влияние выключения целой стойки и выяснения характерных скоростей перехода кластера в стационарный режим. При этом, численно решая дифференциальные уравнения процессов, можно наглядно рассмотреть динамику чанков и нод.
Каждый диск имеет несколько отличающиеся характеристики чтения/записи, включая латентность и пропускную способность. Тем не менее, можно более точно оценивать константы скоростей процессов, интегрируя по соответствующим функциям распределения характеристик дисков, по аналогии с константами скоростей в газах, проинтегрированные по максвелловскому распределению по скоростям.

Таким образом, кинетический подход позволяет, с одной стороны, получить простое описание и аналитические зависимости, с другой стороны — обладает весьма серьезным потенциалом для введения дополнительных тонких факторов и процессов, основываясь на анализе данных работы кластера, добавляя специфические моменты по необходимости. Имеется возможность оценивать влияние вклада каждого фактора на результирующие уравнения, позволяя моделировать улучшения с целью их целесообразности. В простейшем случае такая модель позволяет быстро получать аналитические зависимости, давая рецепты по улучшению ситуации. При этом моделирование может иметь двунаправленный характер: можно итеративно улучшать модель, добавляя процессы в систему кинетических уравнений; так и пытаться проанализировать потенциальные улучшения системы, вводя в модель соответствующие процессы. Т.е. проводить моделирование улучшений до непосредственной дорогостоящей реализации их в коде.

Кроме того, всегда можно перейти к численному интегрированию системы жестких нелинейных дифференциальных уравнений, получив динамику и отклик системы на конкретные воздействия или малые возмущения.

Таким образом, синергия, казалось бы, не связанных между собой областей знаний позволяет получить удивительные результаты, обладающие неоспоримой предсказательной силой.

Григорий Демченко, разработчик YT

Литература

[1] Cap Theorem Myths
[2] Spanner, TrueTime and the CAP Theorem
[3] The probability of data loss in large clusters
[4] Химическая кинетика
[5] Активированного комплекса теория
[6] Приближенные методы химической кинетики
[7] Распределение Максвелла
[8] YT: зачем Яндексу своя MapReduce-система и как она устроена

Теги:

Хабы:

Если эта публикация вас вдохновила и вы хотите поддержать автора — не стесняйтесь нажать на кнопку

Кинетика больших кластеров

Краткое содержание

Моделирование кластера

Чанки

Планирование репликации

Обсуждение предельных случаев

Сравнение подходов

Потеря чанка

Выводы

Публикации

Истории

Работа

Ближайшие события