На хабре нет ни одной статьи о поиске компонент сильной связности. Однако это интересная задача, имеющая приложения в самых разных сферах: системах рекомендаций, математической логике и, неожиданно, экологии. Ниже формулировка задачи и решение — алгоритм Косарайю.
К делу:
Заметим: отношение сильной связности — это отношение эквивалентности.



Компонентой сильной связности называется класс эквивалентности множества вершин ориентированного графа относительно отношения сильной связности. Другими словами компонента сильной связности = сильно связный подграф. Так как сильная связность — это отношение эквивалентности, то граф разбивается на сильно связные компоненты. Наша задача найти все такие классы эквивалентности.
Алгоритм Косарайю
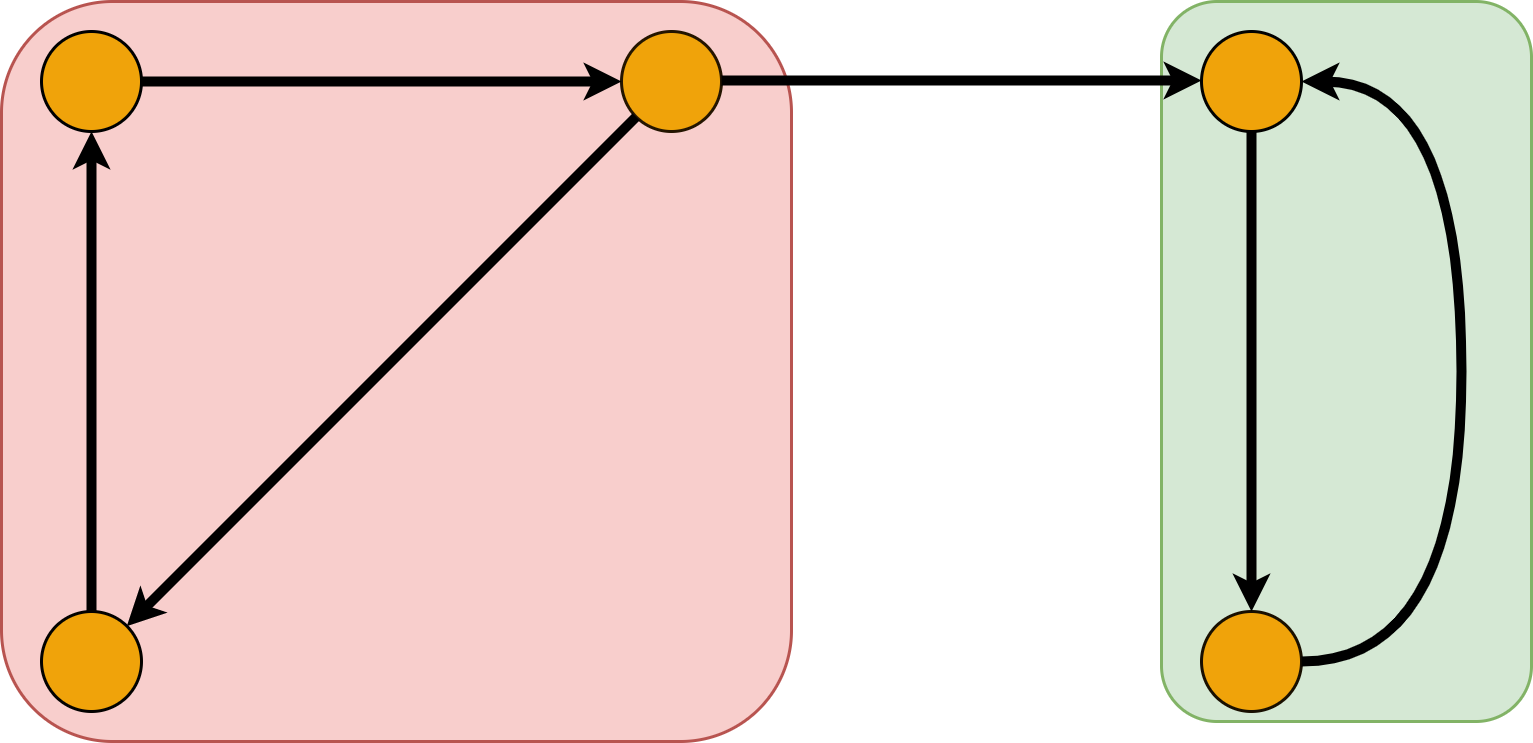
Метод Косарайю прост для реализации и понимания. Так как компоненты сильной связности есть циклы, то они совпадают и у исходного графа и у его инвертирования.
Пусть дан ориентированный граф G = (V, E). Через G' = (V, E') обозначим интертирование G.
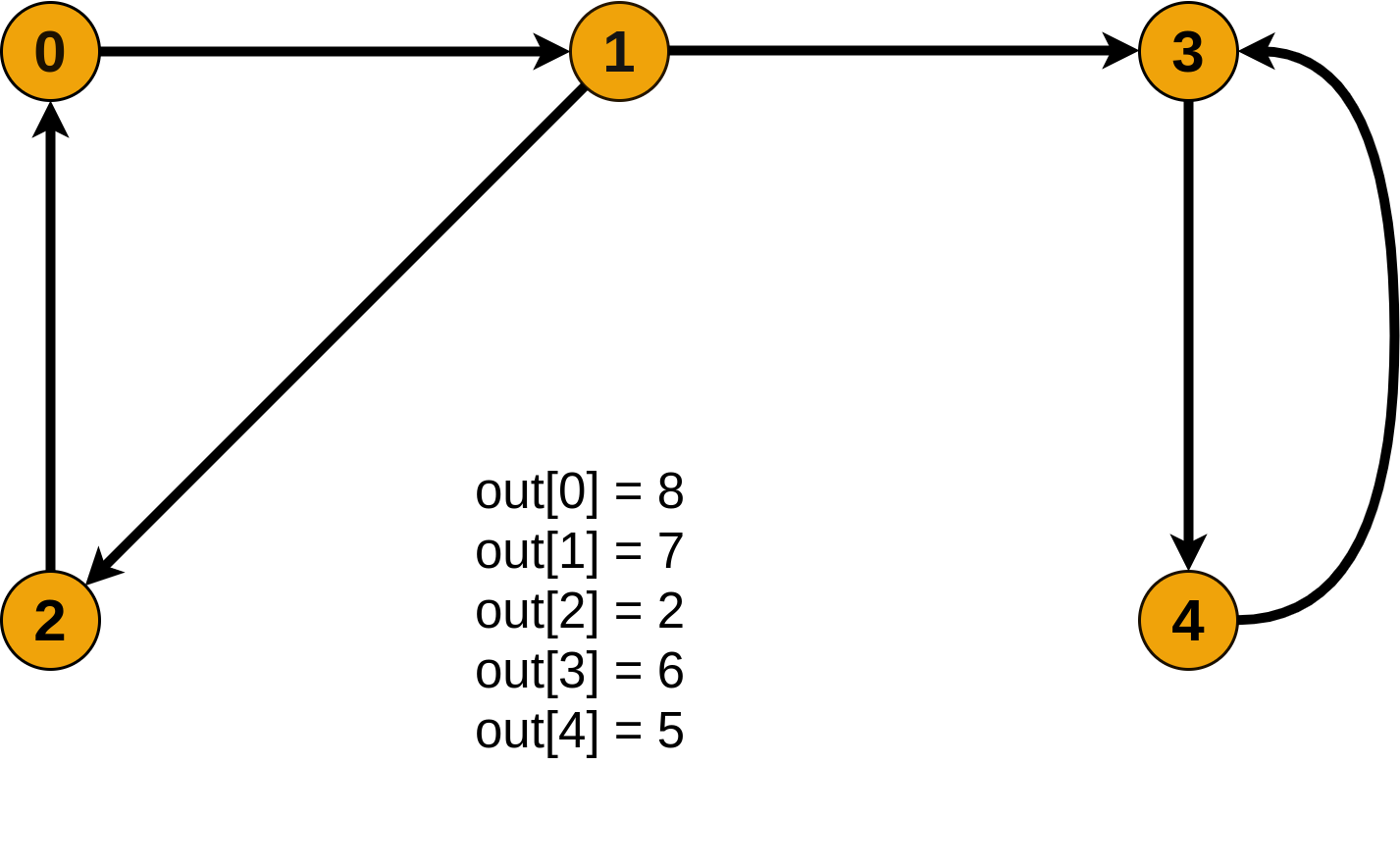
Будем обходить граф G в глубину, пока не посетим все вершины. Заведем массив out = [0...|V|-1] — время выхода из вершины. Под временем понимаются логические часы: изначально время равно 0, при переходе в вершину или выходе из неё время увеличивается на 1.
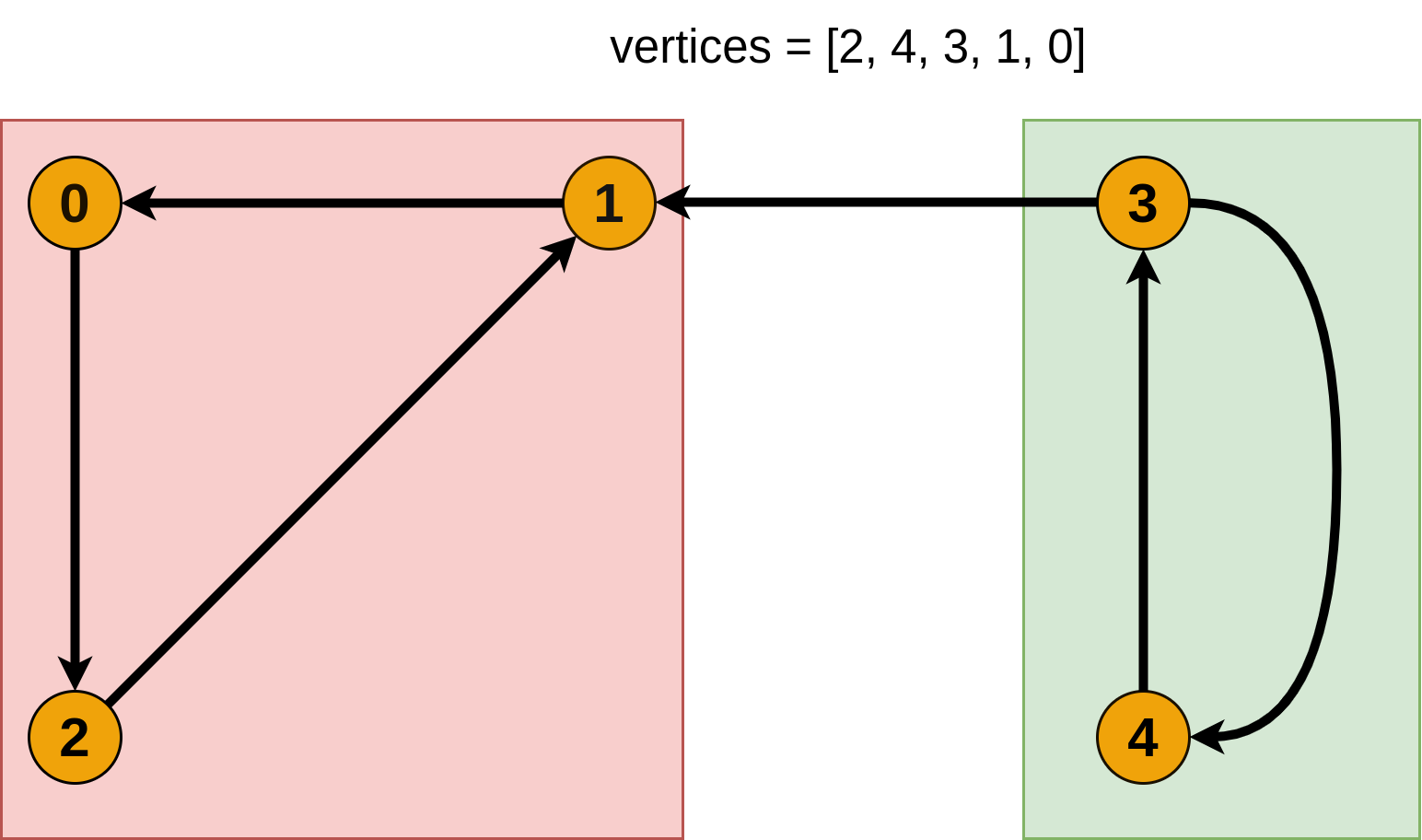
Когда обход закончится, заведем массив vertices, куда добавим все вершины в порядке увеличения времени выхода. Теперь запустим обход в глубинку на инвертированном графе G'. Каждый раз для обхода будем выбирать ещё не посещенную вершину с максимальным индексом в массиве vertices. Все вершины, посещенные в ходе одной итерации dfs, образуют компоненту сильной связности.
Время работы
Заметим: если граф представлен графом смежности, то нам не требуетcя хранить в памяти инвертированный граф. Иначе нам потребуется O(V+E) доп. памяти. Но, в любом случае, нам требуется O(V) памяти для массивов out и vertices.
Алгоритм состоит из двух обходов DFS. Каждый работает пропорционально V+E для разреженных графов и V^2 для насыщенных. Кроме того, нам требуется O(VlogV) для сортировки вершин при построении массива vertices.
Дополнительно
Корректность алгоритма и псевдокод можно посмотреть тут: www.jeffreykarres.com/blog/kosaraju
В начале статьи я упоминал приложения.
К делу:
- Две вершины (
и
) ориентированного графа называют сильно связными, если существует путь из
в
и существует путь из
в
.
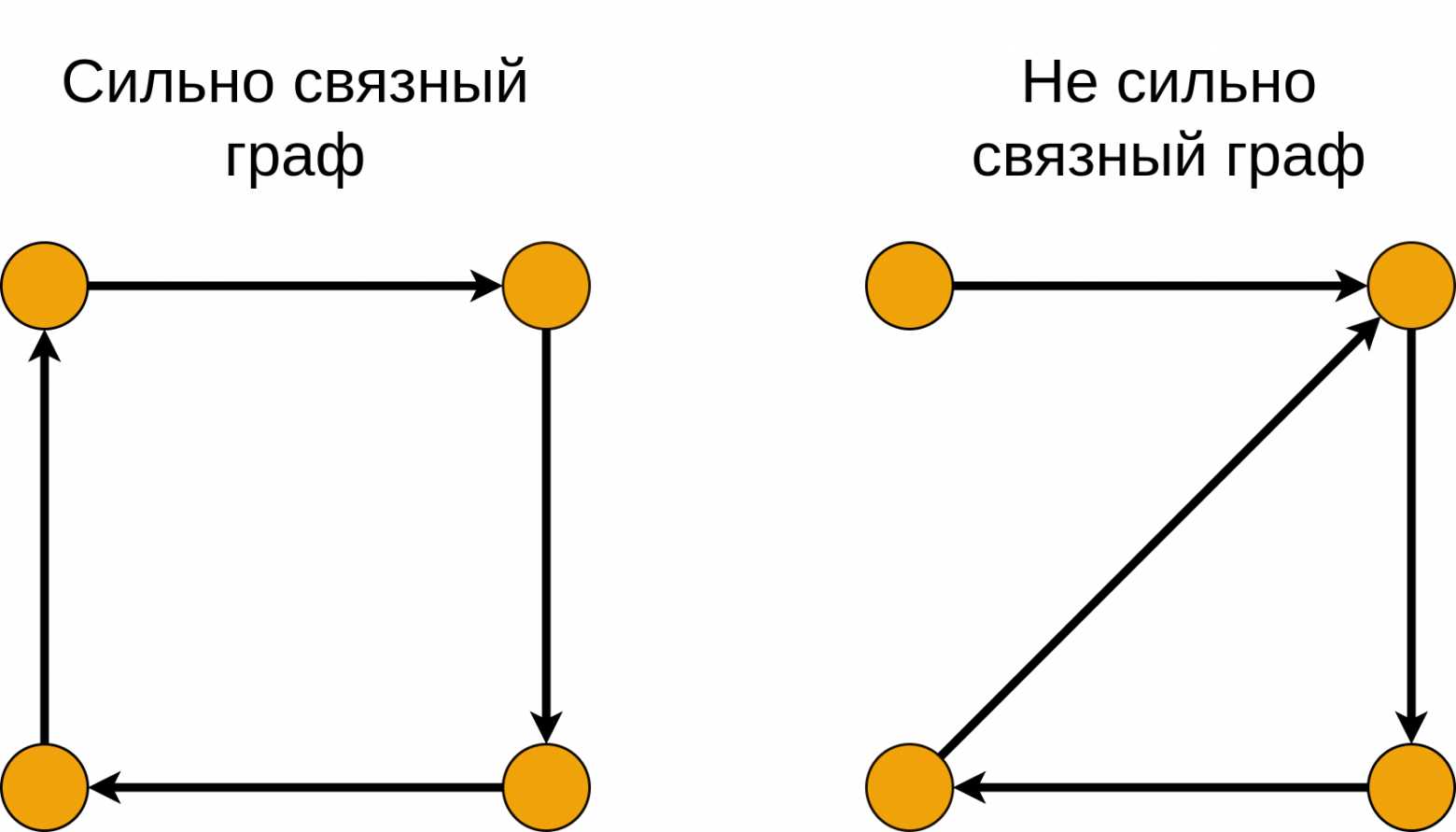
- Ориентированный граф называется сильно связным, если любые две его вершины сильно связны.

Заметим: отношение сильной связности — это отношение эквивалентности.
Компонентой сильной связности называется класс эквивалентности множества вершин ориентированного графа относительно отношения сильной связности. Другими словами компонента сильной связности = сильно связный подграф. Так как сильная связность — это отношение эквивалентности, то граф разбивается на сильно связные компоненты. Наша задача найти все такие классы эквивалентности.

Алгоритм Косарайю
- Инвертированием ориентированного графа назовем процедуру, в ходе которой поменяем направление каждого ребра на противоположное.
Метод Косарайю прост для реализации и понимания. Так как компоненты сильной связности есть циклы, то они совпадают и у исходного графа и у его инвертирования.
Пусть дан ориентированный граф G = (V, E). Через G' = (V, E') обозначим интертирование G.
Будем обходить граф G в глубину, пока не посетим все вершины. Заведем массив out = [0...|V|-1] — время выхода из вершины. Под временем понимаются логические часы: изначально время равно 0, при переходе в вершину или выходе из неё время увеличивается на 1.

Когда обход закончится, заведем массив vertices, куда добавим все вершины в порядке увеличения времени выхода. Теперь запустим обход в глубинку на инвертированном графе G'. Каждый раз для обхода будем выбирать ещё не посещенную вершину с максимальным индексом в массиве vertices. Все вершины, посещенные в ходе одной итерации dfs, образуют компоненту сильной связности.

Время работы
Заметим: если граф представлен графом смежности, то нам не требуетcя хранить в памяти инвертированный граф. Иначе нам потребуется O(V+E) доп. памяти. Но, в любом случае, нам требуется O(V) памяти для массивов out и vertices.
Алгоритм состоит из двух обходов DFS. Каждый работает пропорционально V+E для разреженных графов и V^2 для насыщенных. Кроме того, нам требуется O(VlogV) для сортировки вершин при построении массива vertices.
Дополнительно
Корректность алгоритма и псевдокод можно посмотреть тут: www.jeffreykarres.com/blog/kosaraju
В начале статьи я упоминал приложения.
- На SO писали про использование этого алгоритма для формальной верификации:
stackoverflow.com/questions/11212676/what-are-strongly-connected-components-used-for
- А про экологию можно почитать в статье:
www.nceas.ucsb.edu/~allesina/PDF/Allesina2005.pdf
