Часть 4. Введение в градиентный спуск
Эта часть представляет собой теоретическое введение в инверсную кинематику и содержит программное решение, основанное на градиентном спуске (gradient descent). Эта статья не будет всеобъемлющим руководством по этой теме, это всего лишь общее введение. В следующей части мы покажем настоящую реализацию этого алгоритма на C# в Unity.
Серия состоит из следующих частей (части 1-3 представлены в предыдущем посте):
- Часть 1. Введение в процедурную анимацию
- Часть 2. Математика прямой кинематики
- Часть 3. Реализация прямой кинематики
- Часть 4. Введение в градиентный спуск
- Часть 5. Инверсная кинематика для робота-манипулятора
- Часть 6. Инверсная кинематика щупалец
Часть 7. Инверсная кинематика лап паука
Введение
В предыдущей части серии («Реализация прямой кинематики») представлено решение проблемы прямой кинематики. У нас получилась функция
ForwardKinematics, определяющая точку в пространстве, которой в данный момент касается робот-манипулятор.Если у нас есть конкретная точка в пространстве, которой мы хотим достичь, то можно использовать
ForwardKinematics для оценки близости к ней манипулятора с учётом текущей конфигурации соединений. Расстояние от цели — это функция, которую можно реализовать следующим образом:public Vector3 DistanceFromTarget(Vector3 target, float [] angles) { Vector3 point = ForwardKinematics (angles); return Vector3.Distance(point, target); }
Нахождение решения проблемы инверсной кинематики означает, что нам нужно минимизировать значение, возвращаемое функцией
DistanceFromTarget. Минимизация функции — это одна из широко известных проблем, и в программировании, и в математике. Подход, который мы будем использовать, основан на технике под названием градиентный спуск (Wikipedia). Несмотря на то, что она не является самой эффективной, техника имеет свои преимущества: она не специфична для решения конкретной проблемы и для неё достаточно знаний, имеющихся у большинства программистов.Аналитическое решение инверсной кинематики
Градиентный спуск — это алгоритм оптимизации. Его можно использовать для всех проблем, не имеющих точного уравнения. Это не наш случай, ведь мы уже вывели уравнение прямой кинематики в части «Математика прямой кинематики»:

Расстояние от целевой точки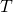 задаётся как:
задаётся как:
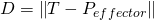
где — это евклидова норма вектора
— это евклидова норма вектора 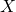 .
.
Аналитическое решение этой проблемы можно найти минимизацией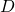 , которая является функцией
, которая является функцией 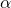 .
.
Есть и другие, более структурированные подходы к решению проблемы инверсной кинематики. Для начала стоит взглянуть на матрицы Денавита-Хартенберга (Wikipedia).

Расстояние от целевой точки
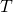 задаётся как:
задаётся как: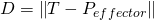
где
 — это евклидова норма вектора
— это евклидова норма вектора 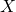 .
.Аналитическое решение этой проблемы можно найти минимизацией
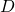 , которая является функцией
, которая является функцией 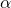 .
.Есть и другие, более структурированные подходы к решению проблемы инверсной кинематики. Для начала стоит взглянуть на матрицы Денавита-Хартенберга (Wikipedia).
Градиентный спуск
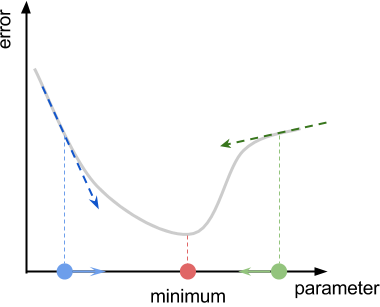
Простейший способ разобраться в работе градиентного спуска — представить холмистый рельеф. Мы находимся в случайном месте и хотим достигнуть самой низкой точки. Назовём её минимумом рельефа. На каждом шаге градиентный спуск говорит нам двигаться в направлении, снижающем нашу высоту. Если геометрия рельефа относительно проста, то такой подход приведёт нас к самому низу долины.
На графике ниже показан стандартный случай, в котором градиентный спуск будет успешным. В этом простейшем примере у нас есть функция. Она получает один параметр (ось X) и возвращает значение ошибки (ось Y). Мы начинаем со случайной точки на оси X (синяя и зелёная точки). Градиентный спуск должен заставить нас двигаться в направлении минимума (синяя и зелёная стрелки).
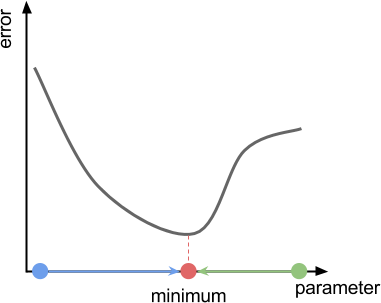
Если мы будем смотреть на функцию в целом, то направление движения очевидно. К сожалению, градиентный спуск не имеет заранее информации о том, где находится минимум. Лучшей догадкой, которую может допустить алгоритм, станет движение по направлению к склону, также называемом градиентом функции. Если вы находитесь на горе, отпустите мяч, и он сам достигнет долины. На графике ниже показан градиент функции ошибок в двух разных точках.
Насколько хорошо выглядит рельеф?
Чтобы градиентный спуск был эффективным, минимизируемая нами функция должна удовлетворять определённым требованиям. Если рельеф функции относительно плавный, то вероятность успешного применения градиентного спуска выше. Если у функции есть разрывы или множество максимумов, то это особенно сложно, потому что для достижения дна долины потребуется гораздо более долгое путешествие.
Вот как может выглядеть рельеф для робота-манипулятора с двумя соединениями (управляемыми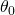 и
и 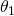 ):
):
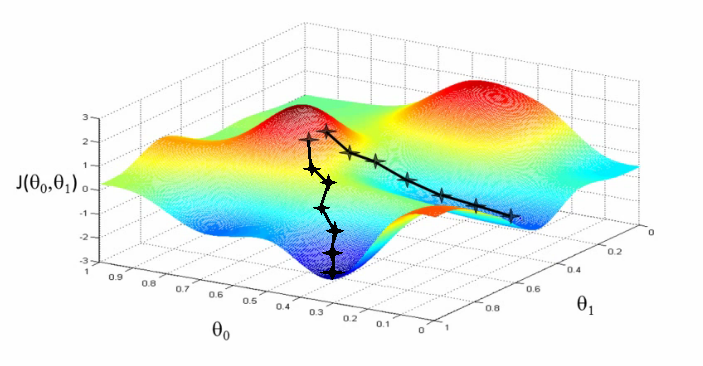
Вот как может выглядеть рельеф для робота-манипулятора с двумя соединениями (управляемыми
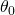 и
и 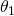 ):
):
Оценка градиента
Если вы изучали математический анализ, то, наверно, знаете, что градиент функции непосредственно связан с её производной. Однако для вычисления производной функции необходимо, чтобы она удовлетворяла определённым математическим свойствам, и выполнение этого требования для любой проблемы в общем случае гарантировать невозможно. Более того, для аналитического взятия производной нужно, чтобы функция ошибок была представлена в аналитическом виде. И у нас не всегда есть аналитический вид функции, которую нужно минимизировать.
Во всех таких случаях невозможно найти истинную производную функции. Решением является приблизительная оценка её значения. На графике ниже показано, как она находится в одном измерении. Дискретной выборкой близлежащих точек можно приблизительно получить локальный градиент функции. Если функция ошибок меньше слева, то мы двигаемся влево, если справа — то вправо.
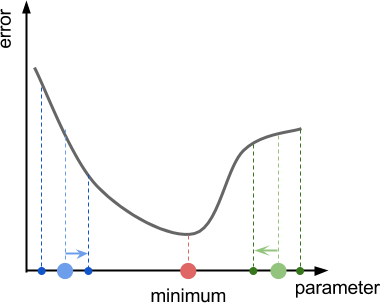
В чём разница между градиентом и производной?
Понятия градиента и произвольной тесно связаны.
Градиент или косая производная функции — это вектор, указывающий в направлении наискорейшего подъёма. В случае одномерных функций (как на наших графиках) градиент равен или , если функция идёт вверх, или
, если функция идёт вверх, или 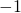 , если функция идёт вниз. Если функция определена через две переменные (например, робот-манипулятор с двумя соединениями), то градиент является «стрелкой» (единичным вектором) двух элементов, направленным в сторону наискорейшего подъёма.
, если функция идёт вниз. Если функция определена через две переменные (например, робот-манипулятор с двумя соединениями), то градиент является «стрелкой» (единичным вектором) двух элементов, направленным в сторону наискорейшего подъёма.
Производная функции, в отличие от градиента — это просто число, определяющее скорость подъёма функции при движении в направлении градиента.
В этой статье мы не будем стремиться вычислить настоящий градиент функции. Вместо этого мы создадим оценку. Наш приблизительный градиент — это вектор, который, как мы надеемся, указывает в направлении наискорейшего подъёма. Как мы увидим, это необязательно будет единичный вектор.
Градиент или косая производная функции — это вектор, указывающий в направлении наискорейшего подъёма. В случае одномерных функций (как на наших графиках) градиент равен или
 , если функция идёт вверх, или
, если функция идёт вверх, или 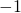 , если функция идёт вниз. Если функция определена через две переменные (например, робот-манипулятор с двумя соединениями), то градиент является «стрелкой» (единичным вектором) двух элементов, направленным в сторону наискорейшего подъёма.
, если функция идёт вниз. Если функция определена через две переменные (например, робот-манипулятор с двумя соединениями), то градиент является «стрелкой» (единичным вектором) двух элементов, направленным в сторону наискорейшего подъёма.Производная функции, в отличие от градиента — это просто число, определяющее скорость подъёма функции при движении в направлении градиента.
В этой статье мы не будем стремиться вычислить настоящий градиент функции. Вместо этого мы создадим оценку. Наш приблизительный градиент — это вектор, который, как мы надеемся, указывает в направлении наискорейшего подъёма. Как мы увидим, это необязательно будет единичный вектор.
Насколько важно создание выборки?
Оно очень важно. Выборка близлежащих точек требует оценки функции на определённом расстоянии от текущего положения. Это расстояние критически важно.
Посмотрите на график:
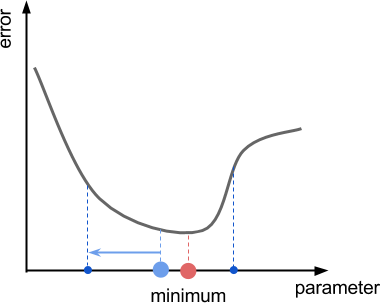
Это расстояние выборки, использованное для оценки градиента, слишком велико. Градиентный спуск ошибочно «предполагает», что правая сторона выше, чем левая. В результате алгоритм будет двигаться в неправильном направлении.
Снижение расстояния выборки позволяет уменьшить эту проблему, но избавиться от неё никогда не удастся. Более того, меньшее расстояние выборки приводит ко всё более медленному приближению к решению.
Эту проблему можно решить с помощью более сложных вариаций градиентных спусков.
Посмотрите на график:

Это расстояние выборки, использованное для оценки градиента, слишком велико. Градиентный спуск ошибочно «предполагает», что правая сторона выше, чем левая. В результате алгоритм будет двигаться в неправильном направлении.
Снижение расстояния выборки позволяет уменьшить эту проблему, но избавиться от неё никогда не удастся. Более того, меньшее расстояние выборки приводит ко всё более медленному приближению к решению.
Эту проблему можно решить с помощью более сложных вариаций градиентных спусков.
Что если у функции есть несколько локальных минимумов?
В общем случае такой «жадный» подход не даёт нам никаких гарантий, что мы на самом деле достигнем самой низкой точки долины. Если есть другие долины, то мы можем застрять в одной из них и не сможем достичь нашей истинной цели.
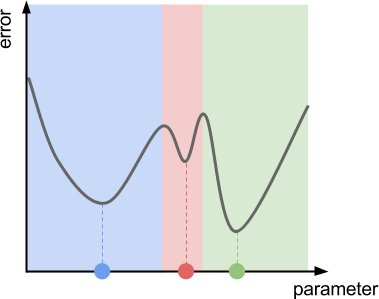
С учётом изложенного выше наивного описания градиентного спуска мы можем заметить, что именно это произойдёт с функцией на графике выше. У этой функции есть три локальных минимума, создающих три отдельные долины. Если мы инициализируем градиентный спуск в точке из зелёной области, то он закончится на дне зелёной долины. То же самое относится к красной и синей областям.
Все эти проблемы тоже можно решить с помощью усложнённых вариаций градиентного спуска.

С учётом изложенного выше наивного описания градиентного спуска мы можем заметить, что именно это произойдёт с функцией на графике выше. У этой функции есть три локальных минимума, создающих три отдельные долины. Если мы инициализируем градиентный спуск в точке из зелёной области, то он закончится на дне зелёной долины. То же самое относится к красной и синей областям.
Все эти проблемы тоже можно решить с помощью усложнённых вариаций градиентного спуска.
Математика
Теперь, когда у нас есть общее понимание графической работы градиентного спуска, давайте посмотрим, как перевести его на язык математики. Первый этап — вычисление градиента нашей функции ошибок
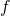 в конкретной точке
в конкретной точке 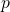 . Нам требуется найти направление, в котором растёт функция. Градиент функции тесно связан с её производной. Поэтому неплохо бы начать создание нашей оценки с изучения того, как вычисляется производная.
. Нам требуется найти направление, в котором растёт функция. Градиент функции тесно связан с её производной. Поэтому неплохо бы начать создание нашей оценки с изучения того, как вычисляется производная.С математической точки зрения производная функции
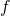 называется
называется 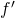 . Её значение в точке
. Её значение в точке 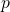 равно
равно 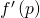 , и оно показывает, насколько быстро растёт функция. Согласно ей:
, и оно показывает, насколько быстро растёт функция. Согласно ей: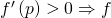 локально растёт вверх;
локально растёт вверх;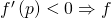 локально опускается вниз;
локально опускается вниз; локально плоская.
локально плоская.
Идея заключается в том, чтобы использовать оценку
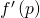 для вычисления градиента, обозначаемого
для вычисления градиента, обозначаемого 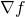 . Математически
. Математически 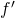 определяется как:
определяется как: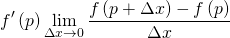
На графике ниже показано, что это значит:
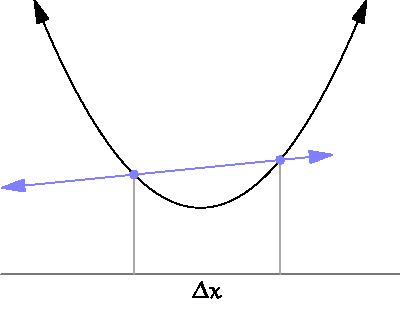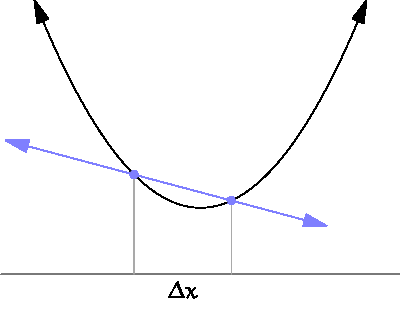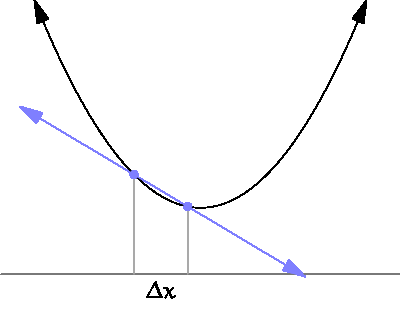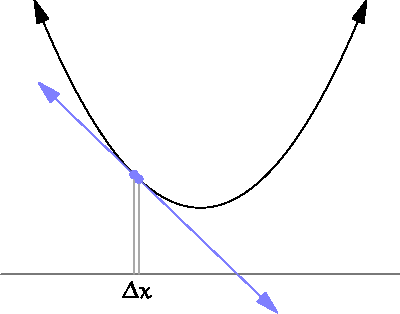
В нашем случае для оценки производной нам нужно выполнить выборку функции ошибок в двух разных точках. Небольшое расстояние между ними
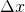 — это расстояние выборки, о котором мы говорили в предыдущем разделе.
— это расстояние выборки, о котором мы говорили в предыдущем разделе.Подведём итог. Для вычисления истинной производной функции необходимо использовать предел. Наш градиент является приблизительной оценкой производной, созданной с помощью достаточно небольшого расстояния выборки:
- Производная
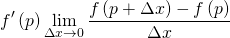
- Приблизительный градиент
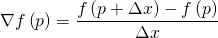
В следующем разделе мы увидим, чем эти два понятия отличаются при нескольких переменных.
Найдя приблизительную производную, нам нужно двигаться в противоположном направлении, чтобы спуститься по функции вниз. Это значит, что нужно обновить параметр
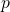 след��ющим образом:
след��ющим образом: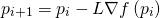
Константу
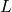 часто называют learning rate. Она определяет, как быстро мы будем двигаться по градиенту. Чем больше значения, тем быстрее найдётся решение, но тем больше вероятность пропустить его.
часто называют learning rate. Она определяет, как быстро мы будем двигаться по градиенту. Чем больше значения, тем быстрее найдётся решение, но тем больше вероятность пропустить его.lim?
Если вы не изучали математический анализ, то можете быть не знакомы с понятием пределов. Пределы — это математическое средство, позволяющее нам достичь бесконечности.
Рассмотрим наш условный пример. Чем меньше расстояние выборки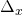 , тем лучше мы можем оценить истинный градиент функции. Однако мы не можем задать
, тем лучше мы можем оценить истинный градиент функции. Однако мы не можем задать 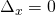 , потому что деление на ноль не разрешено. Пределы позволяют нам обойти эту проблему. Мы не можем делить на ноль, но с помощью пределов мы можем задать число, условно близкое к нулю, но на самом деле ему не равное.
, потому что деление на ноль не разрешено. Пределы позволяют нам обойти эту проблему. Мы не можем делить на ноль, но с помощью пределов мы можем задать число, условно близкое к нулю, но на самом деле ему не равное.
Рассмотрим наш условный пример. Чем меньше расстояние выборки
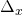 , тем лучше мы можем оценить истинный градиент функции. Однако мы не можем задать
, тем лучше мы можем оценить истинный градиент функции. Однако мы не можем задать 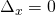 , потому что деление на ноль не разрешено. Пределы позволяют нам обойти эту проблему. Мы не можем делить на ноль, но с помощью пределов мы можем задать число, условно близкое к нулю, но на самом деле ему не равное.
, потому что деление на ноль не разрешено. Пределы позволяют нам обойти эту проблему. Мы не можем делить на ноль, но с помощью пределов мы можем задать число, условно близкое к нулю, но на самом деле ему не равное.Несколько переменных
Найденное нами решение работает в одном измерении. Это значит, что мы дали определение производной функции вида
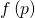 , где
, где 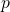 — это одно число. В этом конкретном случае мы можем найти достаточно точное приблизительное значение производной выборкой функции
— это одно число. В этом конкретном случае мы можем найти достаточно точное приблизительное значение производной выборкой функции 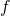 в двух точка��:
в двух точка��: 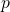 и
и 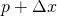 . Результатом является одно число, показывающее увеличение или уменьшение функции. Мы использовали это число в качестве градиента.
. Результатом является одно число, показывающее увеличение или уменьшение функции. Мы использовали это число в качестве градиента.Функция с одним параметром соответствует роботу-манипулятору с единственным сочленением. Если мы хотим выполнить градиентный спуск для более сложных манипуляторов, то необходимо задать градиент функций с несколькими переменными. Например, если у нашего робота-манипулятора есть три сочленения, то функция будет больше похожа на
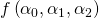 . В таком случае градиент — это вектор, состоящий из трёх чисел, показывающих локальное поведение
. В таком случае градиент — это вектор, состоящий из трёх чисел, показывающих локальное поведение 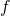 в трёхмерном пространстве его параметров.
в трёхмерном пространстве его параметров.Мы можем ввести понятие частных производных, которые, в сущности, являются «традиционными» производными, вычисляемыми для каждой из переменных:
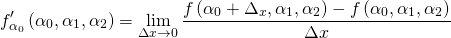
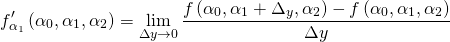
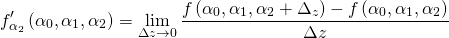
Они представляют собой три различных скалярных числа, каждое из которых показывает, как растёт функция в определённом направлении (или по оси). Для вычисления общего градиента мы аппроксимируем каждую частную производную соответствующим градиентом с помощью достаточно малых расстояний выборки
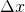 ,
, 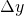 и
и 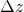 :
: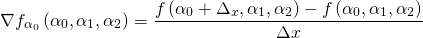
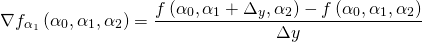
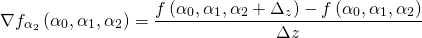
Для нашего градиентного спуска мы будем в качестве градиента использовать вектор, содержащий в себе все три результата:
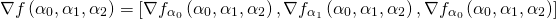
Это не единичный вектор!
Косая производная функции — это единичный вектор, показывающий направление наискорейшего подъёма. Направления — это векторы единичной длины. Однако можно легко заметить, что вычисленный градиент необязательно является единичным вектором.
Хотя это и может выглядеть как насилие над математикой (а возможно, так оно и есть!), но при этом оно не обязательно станет проблемой для нашего алгоритма. Нам нужен вектор, указывающий в направлении наискорейшего подъёма. Использование приблизительных значений частных производных в качестве элементов такого вектора удовлетворяет нашим ограничениям. Если нам нужно, чтобы это был единичный вектор, то можно просто нормализовать его, поделив на его длину.
Использование единичного вектора даёт нам преимущество определения максимальной скорости, с которой мы движемся по поверхности. Эта скорость является learning rate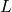 . Использование ненормализованного вектора означает, что мы будем быстрее или медленнее, в зависимости от наклона
. Использование ненормализованного вектора означает, что мы будем быстрее или медленнее, в зависимости от наклона 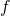 . Это не хорошо и не плохо, это просто ещё один подход к решению нашей проблемы.
. Это не хорошо и не плохо, это просто ещё один подход к решению нашей проблемы.
Хотя это и может выглядеть как насилие над математикой (а возможно, так оно и есть!), но при этом оно не обязательно станет проблемой для нашего алгоритма. Нам нужен вектор, указывающий в направлении наискорейшего подъёма. Использование приблизительных значений частных производных в качестве элементов такого вектора удовлетворяет нашим ограничениям. Если нам нужно, чтобы это был единичный вектор, то можно просто нормализовать его, поделив на его длину.
Использование единичного вектора даёт нам преимущество определения максимальной скорости, с которой мы движемся по поверхности. Эта скорость является learning rate
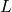 . Использование ненормализованного вектора означает, что мы будем быстрее или медленнее, в зависимости от наклона
. Использование ненормализованного вектора означает, что мы будем быстрее или медленнее, в зависимости от наклона 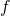 . Это не хорошо и не плохо, это просто ещё один подход к решению нашей проблемы.
. Это не хорошо и не плохо, это просто ещё один подход к решению нашей проблемы.Часть 5. Инверсная кинематика для робота-манипулятора
После долгого путешествия в математику прямой кинематики и геометрического разбора градиентного спуска мы наконец готовы продемонстрировать работающую реализацию проблемы инверсной кинематики. В этой части мы покажем, как её можно применить к роботу-манипулятору, похожему на изображённый ниже.
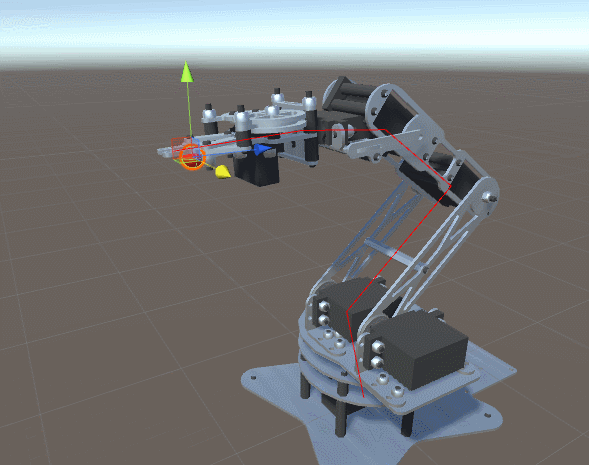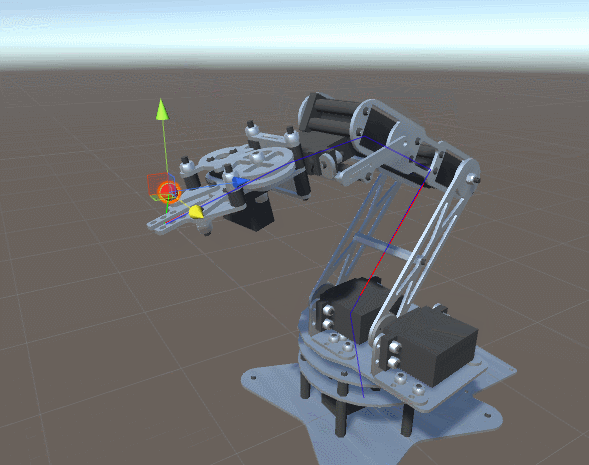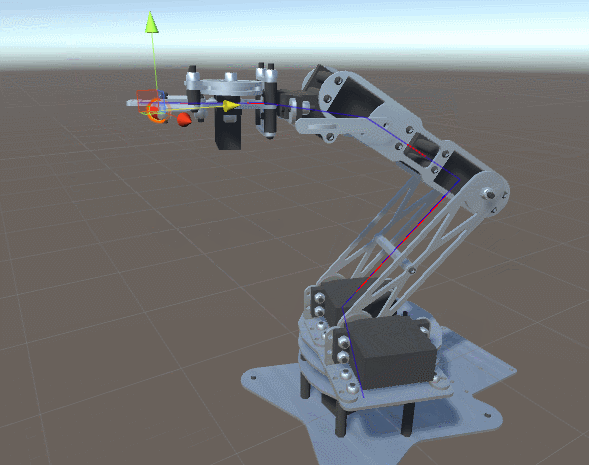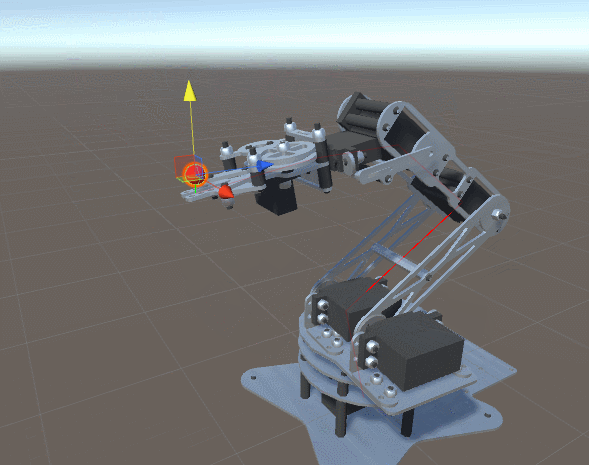
Введение
В предыдущей части изложены математические основы техники под названием градиентный спуск. У нас есть функция
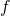 , получающая параметр
, получающая параметр 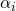 каждого сочленения робота-манипулатора. Этот параметр является текущим углом сочленения. Для заданной конфигурации сочленений
каждого сочленения робота-манипулатора. Этот параметр является текущим углом сочленения. Для заданной конфигурации сочленений 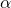 функция
функция 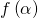 возвращает одно значение, показывающее, насколько далеко конечное звено робота-манипулятора находится от целевой точки
возвращает одно значение, показывающее, насколько далеко конечное звено робота-манипулятора находится от целевой точки 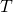 . Наша задача — найти значения
. Наша задача — найти значения 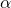 , минимизирующие
, минимизирующие 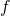 .
.Для этого мы сначала вычислим градиент функции при текущем
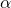 . Градиент — это вектор, показывающий направление наискорейшего подъёма. Проще говоря, это стрелка, указывающая нам направление, в котором растёт функция. Каждый элемент градиента — это приблизительное значение частной производной
. Градиент — это вектор, показывающий направление наискорейшего подъёма. Проще говоря, это стрелка, указывающая нам направление, в котором растёт функция. Каждый элемент градиента — это приблизительное значение частной производной 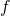 .
.Например, если у робота-манипулятора есть три сочленения, то у нас будет функция
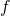 , получающая три параметра:
, получающая три параметра: 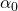 ,
, 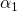 и
и 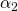 . Тогда наш градиент
. Тогда наш градиент 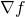 задаётся как:
задаётся как: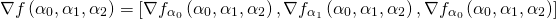
где:
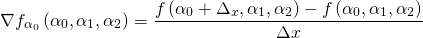
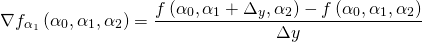
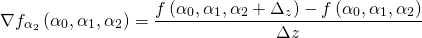
а
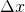 ,
, 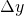 и
и 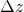 — достаточно малые значения.
— достаточно малые значения.Мы получили приблизительный градиент
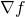 . Если мы хотим минимизировать
. Если мы хотим минимизировать 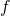 , то необходимо двигаться в противоположном направлении. Это означает обновление
, то необходимо двигаться в противоположном направлении. Это означает обновление 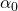 ,
, 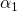 и
и 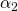 следующим образом:
следующим образом: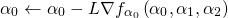
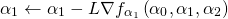
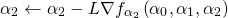
где
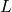 — это learning rate, положительный параметр, управляющий скоростью удаления от поднимающегося градиента.
— это learning rate, положительный параметр, управляющий скоростью удаления от поднимающегося градиента.Реализация
Теперь у нас есть все знания, необходимые для реализации простого градиентного спуска на C#. Давайте начнём с функции, вычисляющей приблизительное значение частного градиента
i-того сочленения. Как говорилось выше, для этого нам нужно создать выборку функции  (которая является нашей функцией ошибок
(которая является нашей функцией ошибок DistanceFromTarget, описанной во «Введении в градиентный спуск») в двух точках:public float PartialGradient (Vector3 target, float[] angles, int i) { // Сохраняет угол, // который будет восстановлен позже float angle = angles[i]; // Градиент: [F(x+SamplingDistance) - F(x)] / h float f_x = DistanceFromTarget(target, angles); angles[i] += SamplingDistance; float f_x_plus_d = DistanceFromTarget(target, angles); float gradient = (f_x_plus_d - f_x) / SamplingDistance; // Восстановление angles[i] = angle; return gradient; }
При вызове этой функции она возвращает одно число, определяющее, как изменяется расстояние от цели как функция от поворота сочленения.
Нам нужно обработать в цикле все сочленения, вычисляя их влияние на градиент.
public void InverseKinematics (Vector3 target, float [] angles) { for (int i = 0; i < Joints.Length; i ++) { // Градиентный спуск // Обновление : Solution -= LearningRate * Gradient float gradient = PartialGradient(target, angles, i); angles[i] -= LearningRate * gradient; } }
Многократный вызов
InverseKinematics перемещает робот-манипулятор ближе к целевой точке.Преждевременное завершение
Одна из основных проблем инверсной кинематики, реализованной этим наивным подходом — малая вероятность окончательного схождения градиента. В зависимости от выбранных для
LearningRate и SamplingDistance значений очень возможно, что манипулятор будет «качаться» рядом с истинным решением.
Так происходит потому, что мы обновляем углы слишком часто, и это приводит к «перелёту» через истинную точку. Правильным решением этой проблемы будет использование адаптивного learning rate, изменяющегося в зависимости от близости к решению. Более дешёвая альтернатива — останавливать алгоритм оптимизации, если мы ближе, чем определённое пороговое значение:
public void InverseKinematics (Vector3 target, float [] angles) { if (DistanceFromTarget(target, angles) < DistanceThreshold) return; for (int i = Joints.Length -1; i >= 0; i --) { // Градиентный спуск // Обновление : Solution -= LearningRate * Gradient float gradient = PartialGradient(target, angles, i); angles[i] -= LearningRate * gradient; // Преждевременное завершение if (DistanceFromTarget(target, angles) < DistanceThreshold) return; } }
Если мы будем повторять эту проверку после каждого поворота сочленения, мы выполним минимальное количество требуемых движений.
Чтобы ещё больше оптимизировать движение манипулятора, мы можем применить градиентный спуск в обратном порядке. Если мы начнём с конечного звена, а не с основания, то это позволит нам совершать более короткие движения. В целом, эти небольшие хитрости позволяют приблизиться к более естественному решению.
Ограничения
Одна из характеристик реальных сочленений заключается в том, что у них обычно есть ограниченный диапазон возможных углов поворота. Не все сочленения могут вращаться на 360 градусов вокруг своей оси. Пока мы не наложили никаких ограничений на наш алгоритм оптимизации. Это значит, что мы, скорее всего, получим вот такое поведение:
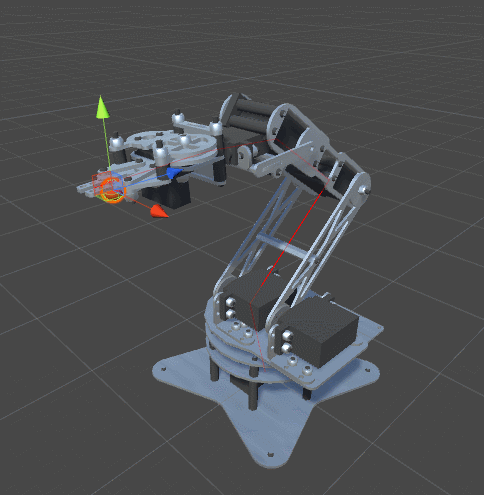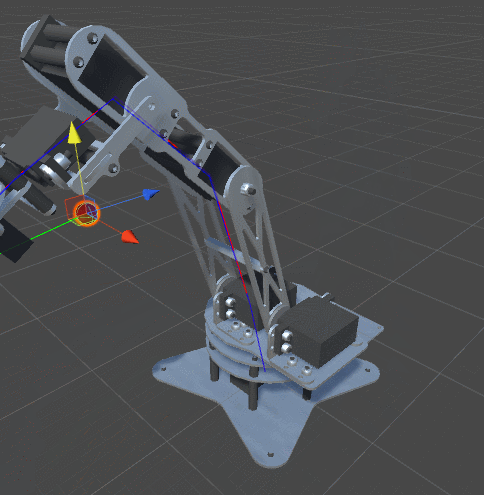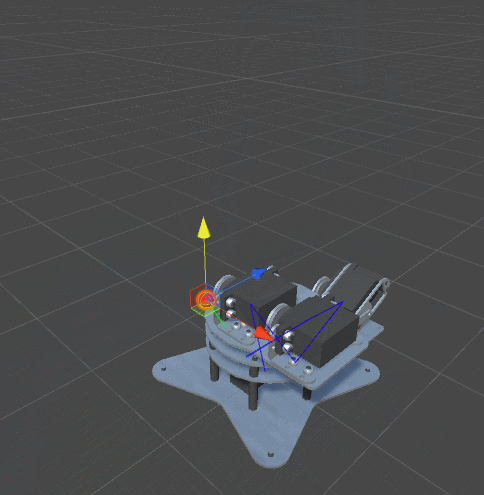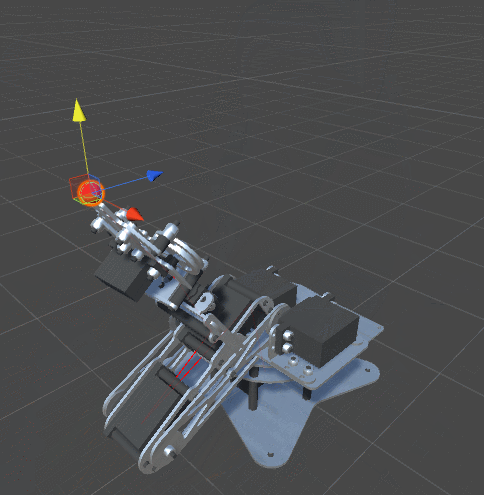
Решение достаточно очевидно. Мы добавим в класс
RobotJoint минимальные и максимальные углы:using UnityEngine; public class RobotJoint : MonoBehaviour { public Vector3 Axis; public Vector3 StartOffset; public float MinAngle; public float MaxAngle; void Awake () { StartOffset = transform.localPosition; } }
затем нужно убедиться, что мы ограничиваем углы нужным диапазоном:
public void InverseKinematics (Vector3 target, float [] angles) { if (DistanceFromTarget(target, angles) < DistanceThreshold) return; for (int i = Joints.Length -1; i >= 0; i --) { // Градиентный спуск // Обновление : Solution -= LearningRate * Gradient float gradient = PartialGradient(target, angles, i); angles[i] -= LearningRate * gradient; // Ограничение angles[i] = Mathf.Clamp(angles[i], Joints[i].MinAngle, Joints[i].MaxAngle); // Преждевременное завершение if (DistanceFromTarget(target, angles) < DistanceThreshold) return; } }
Проблемы
Даже при наличии ограничений углов и преждевременного завершения использованный нами алгоритм очень прост. Слишком прост. С этим решением может возникнуть множество проблем, и большинство из них связано с градиентным спуском. Как написано во «Введении в градиентный спуск», алгоритм может застревать в локальных минимумах. Они являются субоптимальными решениями: неестественными или нежелательными способами достижения цели.
Посмотрите на анимацию:
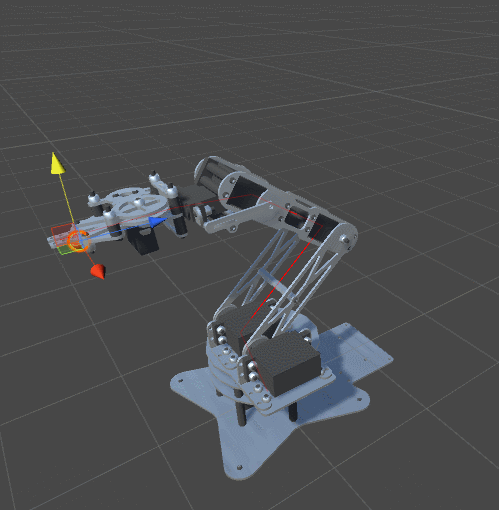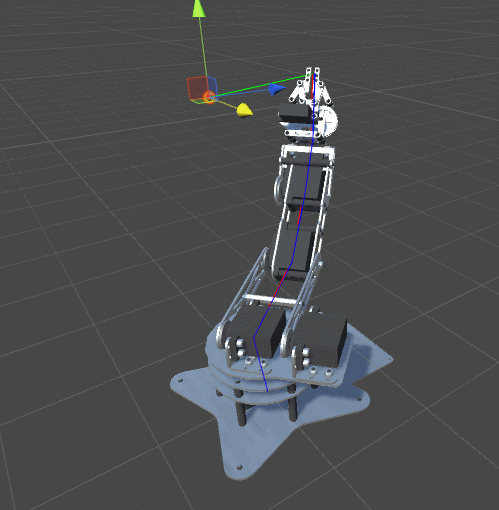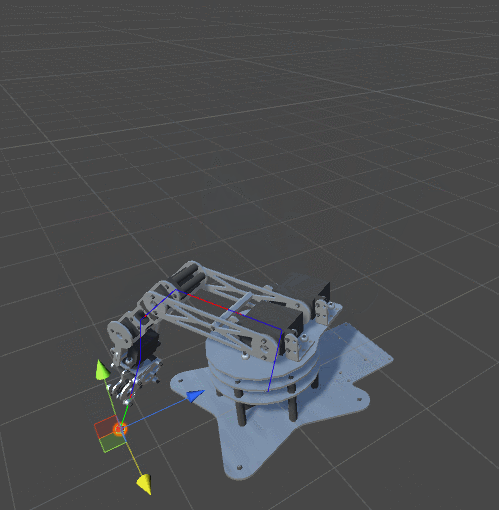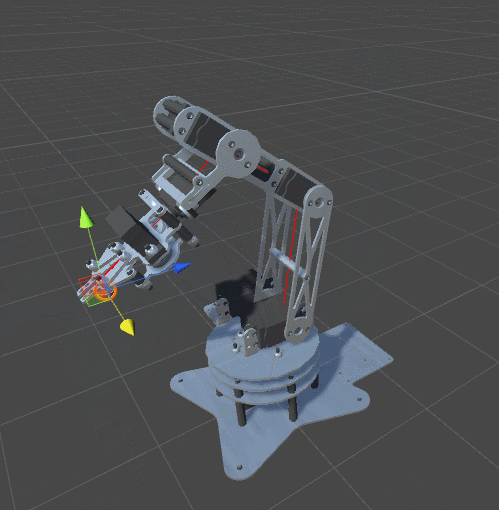
Рука манипулятора ушла слишком далеко, и при возврате в исходное положение она перевернулась. Наилучшим способом избежать этого будет использование функции комфорта. Если мы достигли требуемой точки, то нужно попытаться изменить ориентацию манипулятора на более удобное, естественное положение. Следует заметить, что это не всегда бывает возможно. Изменение ориентации манипулятора может заставить алгоритм увеличить расстояние до цели, что может противоречить его параметрам.
Часть 6. Инверсная кинематика щупалец
Введение
В предыдущей части мы рассмотрели использование градиентного спуска для реализации инверсной кинематики робота-манипулятора. Выполняемое механизмами движение достаточно просто, потому что у них нет сложности настоящих человеческих частей тела. Каждое сочленение робота-манипулятора управляется двигателем. В человеческом теле каждая мышца де-факто является независимым двигателем, который может растягиваться и сокращаться.
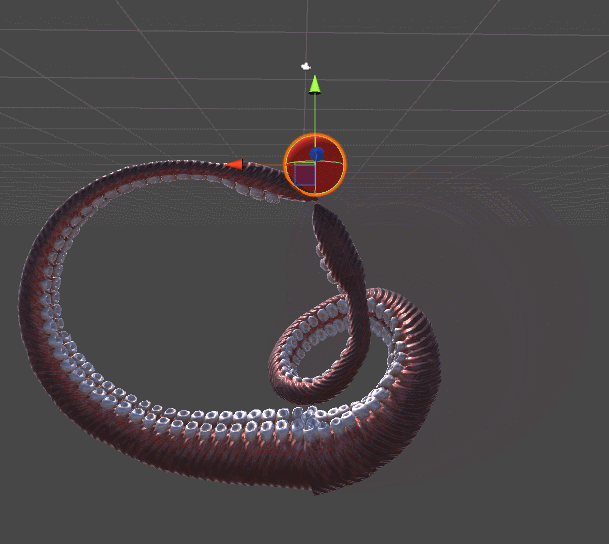
У некоторых существ есть части тела, имеющие несколько степеней свободы. Примером могут служить хобот слона и щупальце осьминога. Моделирование таких частей тела — особо сложная задача, потому что приведённые выше традиционные техники не смогут создать реалистичных результатов.
Мы начнём с примера из предыдущей части и постепенно придём к поведению, которое для наших целей окажется достаточно реалистичным.
Риггинг щупальца
В созданном нами роботе-манипуляторе каждая часть двигалась независимо от других. Щупальца, в отличие от робота, могут изгибаться. Это необходимая особенность, которую нельзя игнорировать, если мы хотим нацелены на реализм. Наше щупальце должно уметь изгибаться.
Компонент Unity, позволяющий реализовать эту функцию, называется Skinned Mesh Renderer:
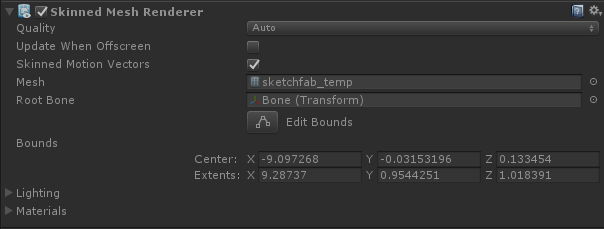
К сожалению, Unity не предоставляет возможности создания рендерера сеток со скиннингом в редакторе. Необходим редактор 3D-моделей, например, Blender. На изображении ниже показана модель щупальца, которое мы будем использовать в этой части. Внутри видно несколько костей, соединённых друг с другом. Это объекты, позволяющие нам изгибать модель.
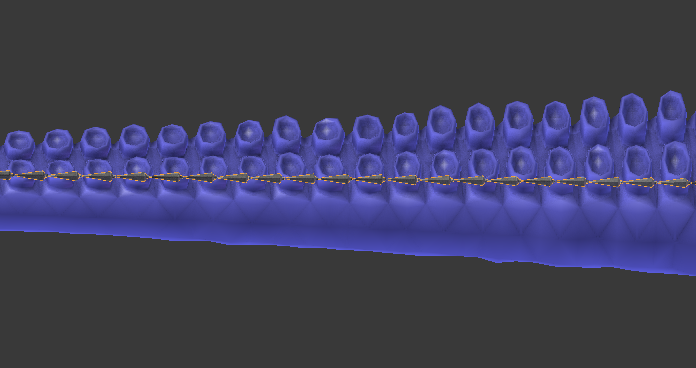
В этом туториале мы не будем изучать добавление костей к моделям, также называемое риггингом. Хорошее введение в предмет можно прочитать в статье Blender 3D: Noob to Pro/Bones.
Кости и сочленения
Следующий этап реализации инверсной кинематики щупальца — прикрепление к каждой кости скрипта
RobotJoint. Благодаря этому мы даём нашему алгоритму инверсной кинематики возможность сгибать щупальце.У обычного осьминога каждое сочленение может свободно поворачиваться по всем трём осям. К сожалению, код написанный для робота-манипулятора, позволяет вращать сочленения только по одной оси. Если попытаться изменить это, то мы добавим нашему коду новый уровень сложности. Вместо этого мы можем циклично менять ось сочленений, чтобы сочленение 0 поворачивалось по X, сочленение 1 — по Y, сочленение 2 — по Z, и так далее. Это может привести к неестественному поведению, но такая проблема у вас может никогда не возникнуть, если кости достаточно малы.
В скачиваемом проекте Unity, продаваемом с этим туториалом, скрипт
SetRobotJointWeights автоматически инициализирует параметры всех сочленений щупальца. Вы можете делать это вручную, чтобы иметь более точный контроль над движением каждой кости.Функция комфорта
На представленной ниже анимации показано два щупальца. Щупальце слева тянется к красной сфере с помощью алгоритма из «Инверсной кинематики для робота-манипулятора». Правое щупальце добавляет совершенно новый уровень реализма, закручиваясь спирально, в более органическом стиле. Этого примера должно быть достаточно, чтобы понять, почему для щупалец нужен свой собственный туториал.
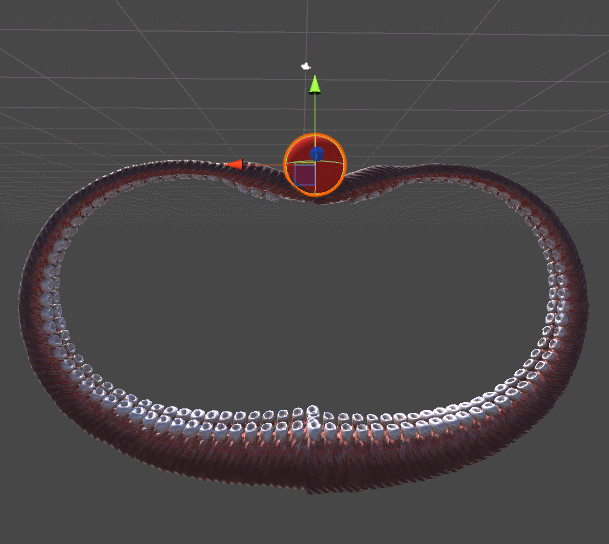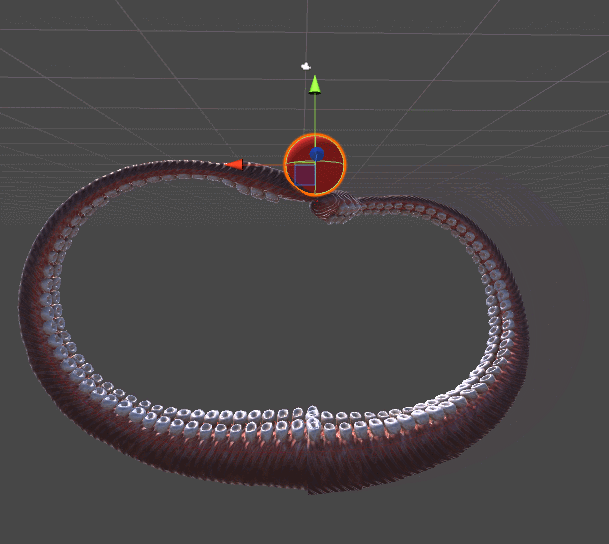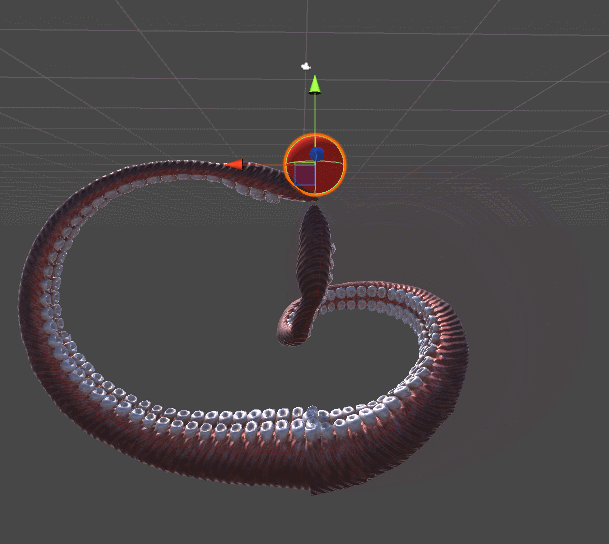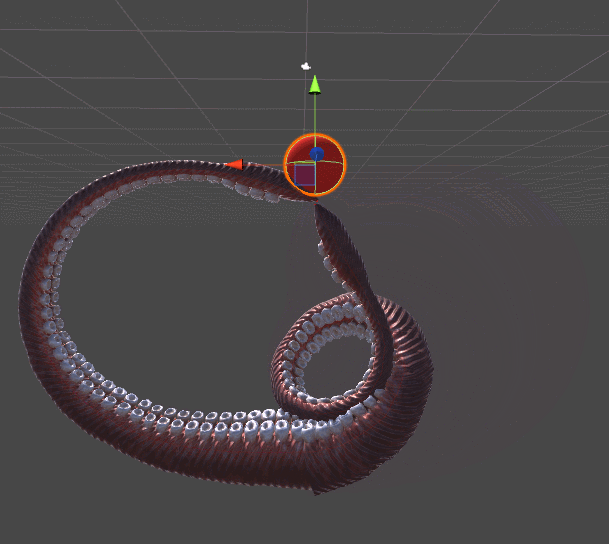
Для обоих щупалец используется градиентный спуск. Разница заключается в функции ошибок, которую они стремятся минимизировать. Механическое щупальце слева просто стремится достать до мяча, её не волнуют все остальные параметры. Как только конечное звено касается мяча, приближение считается завершённым и щупальце просто перестаёт двигаться.
Щупальце справа минимизирует другую функцию. Функция
DistanceFromTarget, использованная для манипулятора, заменена на новую, более сложную функцию. Мы можем заставить эту новую функцию ErrorFunction учитывать и другие параметры, которые нам важны. Показанные в этом туториале щупальца минимизируют три различные функции:- Расстояние до цели: уже готова
- Поворот конечного звена: конец щупальца пытается соответствовать повороту объекта, к которому мы хотим приблизиться. Такое поведение можно заметить в анимации выше, когда правое щупальце спирально загибается вокруг сферы. Поскольку каждое сочленение имеет ограниченный диапазон движений, это создаёт пульсации, распространяющиеся вниз по кинетической цепи костей. Мы можем заставить щупальце соответствовать повороту объекта, к которому она стремится. Для этого мы можем измерить угол между поворотом конечного звена и поворотом цели. В Unity есть для этого удобная функция —
Quaternion.Angle:
float rotationPenalty = Mathf.Abs ( Quaternion.Angle(EndEffector.rotation, Destination.rotation) / 180f );
Такое приведение к соответствию с локальным поворотом не всегда подходит. В зависимости от ситуации можно выравнивать щупальце иначе.
- Кручение: держать части тела неестественным образом некомфортно. Этот параметр «штрафует» криволинейные движения, заставляя инверсную кинематику выполнять более линейный, простой поворот. Для вычисления штрафа за кручение нам нужно сначала определить, что же такое «кручение» в данном контексте. Проще всего определить его как среднее углов для всех сочленений. Такой штраф стремится к тому, чтобы щупальце было расслабленным, и «наказывает» решения, требующие большого количества изгибов.
float torsionPenalty = 0; for (int i = 0; i < solution.Length; i++) torsionPenalty += Mathf.Abs(solution[i]); torsionPenalty /= solution.Length;
Эти три ограничения приводят к более реалистичному способу движения щупалец. Более сложная версия может обеспечить колебания, даже когда условия удовлетворяют всем остальным ограничениям.
Используем разные единицы измерения?
Эти три параметра, скорее всего, будут выражаться в разных единицах измерения. Расстояние до цели может указываться в метрах, а поворот конечного звена — в градусах. Нужно добавить им веса согласно их важности, чтобы разница в десять градусов не считалась такой же плохой, как расстояние в десять метров до цели.
В идеале их нужно нормализовать между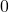 и
и 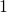 . После этого можно будет использовать коэффициенты для указания их относительной важности:
. После этого можно будет использовать коэффициенты для указания их относительной важности:
Такой подход ещё и обеспечивает более точный контроль за поведением щупальца. В любой момент можно изменить коэффициенты, чтобы менять способ движения в зависимости от ситуации. Например, можно увеличить
В идеале их нужно нормализовать между
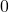 и
и 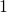 . После этого можно будет использовать коэффициенты для указания их относительной важности:
. После этого можно будет использовать коэффициенты для указания их относительной важности:public float ErrorFunction (Vector3 target, float [] angles) { return NormalisedDistance(target, angles) * DistanceWeight + NormalisedRotation(target, angles) * RotationWeight + NormalisedTorsion (target, angles) * TorsionWeight ; }
Такой подход ещё и обеспечивает более точный контроль за поведением щупальца. В любой момент можно изменить коэффициенты, чтобы менять способ движения в зависимости от ситуации. Например, можно увеличить
TorsionWeight, чтобы распутывать запутавшиеся щупальца.У нас нет аналитического определения!
Традиционную проблему прямой кинематики можно смоделировать аналитически. Это значит, что мы можем вывести уравнение, которое её решает. Мы уже упоминали о существовании аналитических методов решения двойственной проблемы инверсной кинематики.
На данный момент у нас есть функция, которую, возможно, не получится описать аналитически. Если бы мы выбрали традиционный, аналитический подход к решению инверсной кинематики, то нам не удалось бы добавить такие нюансы поведения щупальца. Использование градиентного спуска означает, что теперь мы можем минимизировать (почти!) любую произвольную функцию, есть у неё уравнение или нет.
На данный момент у нас есть функция, которую, возможно, не получится описать аналитически. Если бы мы выбрали традиционный, аналитический подход к решению инверсной кинематики, то нам не удалось бы добавить такие нюансы поведения щупальца. Использование градиентного спуска означает, что теперь мы можем минимизировать (почти!) любую произвольную функцию, есть у неё уравнение или нет.
Усовершенствования
Практически нет никаких ограничений для внесения улучшений в нашу модель. Повысить реализм щупалец определённо поможет функция замедления. Щупальца должны двигаться медленнее, когда приближаются к цели.
Кроме того, щупальца не должны взаимно пересекаться. Чтобы избежать этого, следует использовать коллайдеры для каждого сочленения. Однако это может привести к причудливому поведению. В нашем коде коллизии игнорируются и он может приблизиться к решению, в котором возникают самопересечения. Решение заключается в изменении функции пригодности, чтобы решения с самопересечением имели высокие штрафы.
[Готовый проект Unity со скриптами и 3D-моделями можно приобрести за 10 долларов на странице Patreon автора оригинала статьи.]
К сожалению, оказалось, что ��едьмая часть про поведение паучьих лап у автора ещё не готова. В связи с этим добавил опрос:
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
Нужно ли отдельно переводить статью про инверсную кинематику лап паука, когда она появится?
99.09%Да217
0.91%Нет2
Проголосовали 219 пользователей. Воздержались 17 пользователей.
