Здесь будет рассказано о алгоритме сравнения функций плотности вероятности радиоактивного распада, проявляющих периодичность в звездные сутки и звездный год.
*сидерический год — период орбитального движения Земли вокруг Солнца в инерциальной системе отсчёта (относительно «неподвижных звёзд»);
Эта статья массивное продолжение вводной статьи 2014 года по периодам в радиоактивности
Выводы:
— Форма вероятностей неслучайна и зависит от космофизических причин
— Форма вероятностей с высокой вероятностью повторяется с периодичностью в солнечные и звездные сутки, солнечный и звездный год
— Форма вероятностей сходна в ближайшие промежутки времени
— Формы вероятностей часто бывают хирально симметричными
Академия
Более подробно об этом исследовании написано в книге
И статьях на Успехах физических наук: раз и два.
А теперь сам алгоритм и подробнее про задачу!

Задача стояла так: есть двухнедельный ряд частоты радиоактивного распада в секунду (всего 1639763 секунд {пример 5 секунд: 310 311 299 312 305}). Уже установлено экспертным методом, что паттерны функций плотности вероятности {пример 2 похожих функций вверху абзаца} (по 60 секунд в каждой гистограмме) с хорошей точностью напоминают друг друга каждые 1436 минут {те самые звездные сутки — 23ч 56м}. Требуется подтвердить находку математически.
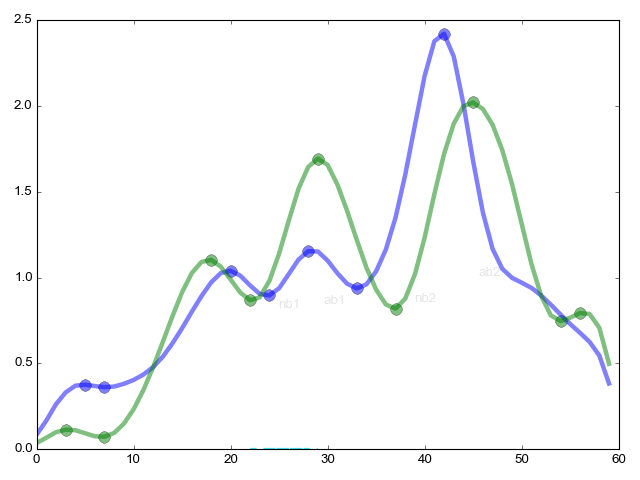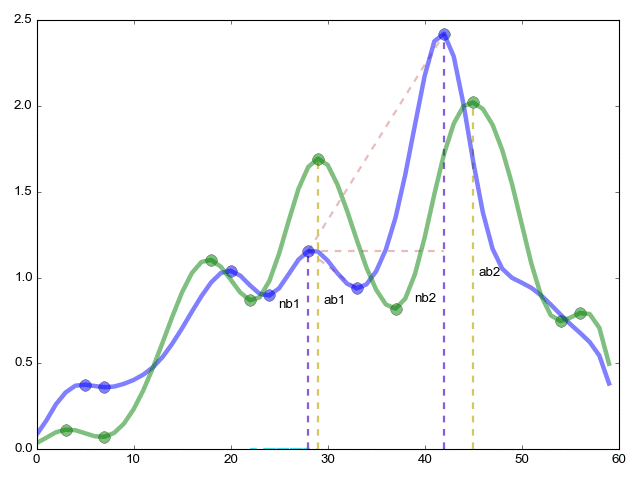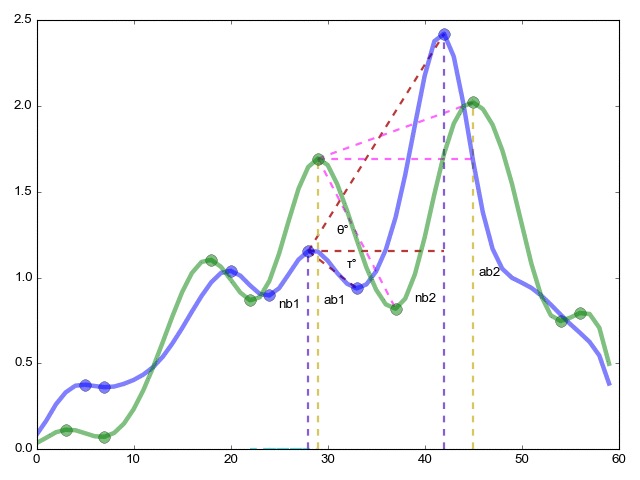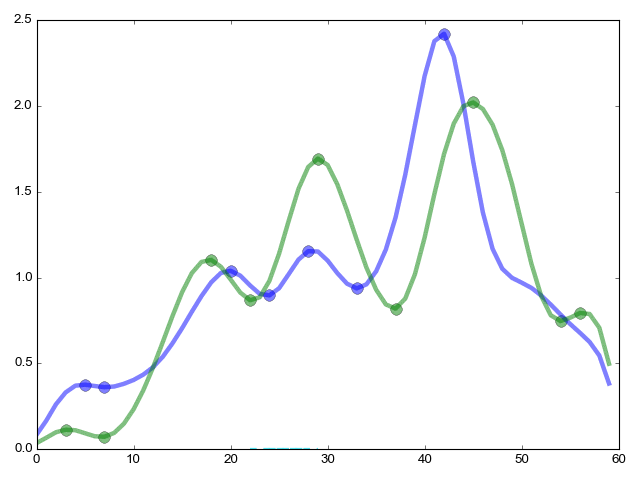
Продолжение функции pikmatch (из дальнего угла статьи) самое важное — комбинаторное сравнение критических точек.
ret=(ab1/ab2)/(nb1/nb2); — Соотношение высоты (y ось) критических точек внутри одной функции к такому же соотношению внутри другой функции
re=(ac1/ac2)/(nc1/nc2) — То же что и в предыдущем случае но теперь по оси x длины между точками
red=(φ°/ξ°)/(θ°/τ°) — В заключении меряем углы
rme=(ab1+1)*(ab2+1)*(nb1+1)*(nb2+1); — коэффициент важности отношения
Теперь финальная формула res=re*red*ret*rme
res — это показатель похожести функции 1 на функцию 2
Вторая часть функции pikmatch()
Перед тем как сравнивать, мы алгоритмом DTW выравниваем одну функцию относительно другой и находим соотвествующие вершины:

Пример евклидова расстояния

И dynamic time warping

Загружаем журнал примеров похожих изображений и создаем функцию бегущего среднего для сглаживания гистограмм до функций плотности вероятности.
Евклидова дистанция, для выравнивание картинки со смещением по горизонтали:
Нахождение пиков:
Метод Dynamic Time Warping для точного соотношения вершин 1 функции вероятности с вершинами 2 функции вероятности:
Теперь применим метод DTW для поиска соответствия вершин одной кривой к другой и если найдена лишняя вершина у одной из функций записываем в вершину пологую точку на кривой с тем же отступом, как будто бы у нас на самом деле там критическая точка.
Заключительная часть кода, где выполняется выравнивание и сравнение 1440 подряд картинок для поиска звездного года. Он найден в +368 минут как и указано в справочнике звездный год = 365.2564 суток
0.2564*1440 минут в сутках = 369.216
1440-1072=368 минут добавляется к году
Так как в python отсчет идет от 0 элемента, то звездные сутки считаются от -3 минут (+1436 минута) от 1440 (+1440 начало нового периода), а звездный год от 1440-1072 минуты.
Примеры похожих картинок:

Несмотря на то что эффект Шноля заявляет о нахождении солнечных суток и солнечного года, таких периодов не было обнаружено.
Звездные сутки были обнаружены в окрестностях +1440 — i минут +1436 минута:
Звездный год — было подсчитаны все сутки от 365 до 366 суток нового года:
1440-1072, 368 то есть +369 дополнительная минута нового года. Точно звездный год 365 дней и 369 минута [365.2564]! (надо учитывать что отсчет начинается с 0 минуты)
Для тех кто решит все сам проверить и возможно улучшить распознавание образов весь код и данные доступны на Github
Спасибо за внимание!
*сидерический год — период орбитального движения Земли вокруг Солнца в инерциальной системе отсчёта (относительно «неподвижных звёзд»);
Эта статья массивное продолжение вводной статьи 2014 года по периодам в радиоактивности
Выводы:
— Форма вероятностей неслучайна и зависит от космофизических причин
— Форма вероятностей с высокой вероятностью повторяется с периодичностью в солнечные и звездные сутки, солнечный и звездный год
— Форма вероятностей сходна в ближайшие промежутки времени
— Формы вероятностей часто бывают хирально симметричными
Академия
Более подробно об этом исследовании написано в книге
И статьях на Успехах физических наук: раз и два.
А теперь сам алгоритм и подробнее про задачу!

Задача стояла так: есть двухнедельный ряд частоты радиоактивного распада в секунду (всего 1639763 секунд {пример 5 секунд: 310 311 299 312 305}). Уже установлено экспертным методом, что паттерны функций плотности вероятности {пример 2 похожих функций вверху абзаца} (по 60 секунд в каждой гистограмме) с хорошей точностью напоминают друг друга каждые 1436 минут {те самые звездные сутки — 23ч 56м}. Требуется подтвердить находку математически.

Продолжение функции pikmatch (из дальнего угла статьи) самое важное — комбинаторное сравнение критических точек.
ret=(ab1/ab2)/(nb1/nb2); — Соотношение высоты (y ось) критических точек внутри одной функции к такому же соотношению внутри другой функции
re=(ac1/ac2)/(nc1/nc2) — То же что и в предыдущем случае но теперь по оси x длины между точками
red=(φ°/ξ°)/(θ°/τ°) — В заключении меряем углы
rme=(ab1+1)*(ab2+1)*(nb1+1)*(nb2+1); — коэффициент важности отношения
Теперь финальная формула res=re*red*ret*rme
res — это показатель похожести функции 1 на функцию 2
Вторая часть функции pikmatch()
for e in range(len(p)+len(p1)): for l in range(len(p)+len(p1)): if e>=len(p): me=minx[e-len(p)];pe=p1[e-len(p)];nme=nm1[e-len(p)]; else: me=maxx[e];pe=p[e];nme=nm[e]; if l>=len(p): ml=minx[l-len(p)];pl=p1[l-len(p)];nml=nm1[l-len(p)]; else: ml=maxx[l];pl=p[l];nml=nm[l]; red1=1;red=1;ab=y[pl]-y[pe];ac=pe-pl;au=x[ml]-x[me];ao=me-ml;hip=math.sqrt(ab**2+ac**2);hipe=math.sqrt(ao**2+au**2); if (hip!=0)and(hipe!=0): if math.asin(abs(au)/hipe)!=0: red=abs(abs(math.asin(abs(ab)/hip)/math.asin(abs(au)/hipe))); # меряем углы ret=abs(1-abs((0.00+abs((y[pl]+0.01)/(y[pe]+0.01)))/(0.00+abs((x[ml]+0.01)/(x[me]+0.01)))));uj=uj+1; re=0+abs(1-abs(float(abs(pe-pl)+1))/float(abs(me-ml)+1));rme=(y[pe]+1)*(y[pl]+1)*(x[me]+1)*(x[ml]+1);rmu+=rme; res+=abs(re*rme*red*ret); return len(pi)*len(pi),res/uj,p,p1; # или /uj? rmu
Перед тем как сравнивать, мы алгоритмом DTW выравниваем одну функцию относительно другой и находим соотвествующие вершины:

Пример евклидова расстояния

И dynamic time warping

Загружаем журнал примеров похожих изображений и создаем функцию бегущего среднего для сглаживания гистограмм до функций плотности вероятности.
ma0=[];ma0.append([line.strip() for line in open('/users/andrejeremcuk/downloads/0505.jnl')]); massa=[];m=[[0] for e in range(len(ma0[0]))];massamyfile=[]; import re t=3;summa=[]; for e in range(3,len(ma0[0])/2): #len(ma0[0]) disguise=re.findall(r":(.+?) ", ma0[0][t]);disguise1=re.findall(r"- #1:(.*)", ma0[0][t]); summa.append(int(disguise[0]));summa.append(int(disguise1[0]));t=t+2; k=0;summ=[];sum1=[]; for e in range(len(summa)/2): summ.append(summa[k]);sum1.append(summa[k+1]);k=k+2; import random import numpy as np from collections import defaultdict import math import matplotlib.pyplot as plt def movingaverage(interval, window_size): window = np.ones(int(window_size))/float(window_size) return np.convolve(interval, window, 'same')
Евклидова дистанция, для выравнивание картинки со смещением по горизонтали:
def euclid(x,y): re=0.0;res=0;a=1 for i in range(len(x)): re=re+abs(x[i]-y[i])**1 return abs((re)/len(x))#,math.sqrt(abs(res));
Нахождение пиков:
def pik(x,y): pikx=[];piky=[];c=0;v=0;cy=0;vy=0;minx=[];miny=[];maxx=[];maxy=[];minmaxx=[];minmaxy=[];#x=x.tolist();y=y.tolist(); for e in range(1,len(x)-2): if (x[e-1]<x[e]>x[e+1])or((x[e-1]<x[e]==x[e+1])and(x[e]>x[e+2])): maxx.append(e);minmaxx.append(e);c+=1; if (x[e-1]>x[e]<x[e+1])or((x[e-1]>x[e]==x[e+1])and(x[e]<=x[e+2])): minx.append(e);minmaxx.append(e);v+=1; if (len(maxx)>1)and(minmaxx[c+v-2]==maxx[c-2])and(minmaxx[c+v-1]==maxx[c-1]): del maxx[c-2];del minmaxx[c+v-2];c-=1; if (len(minx)>1)and(minmaxx[c+v-2]==minx[v-2])and(minmaxx[c+v-1]==minx[v-1]): del minx[v-2];del minmaxx[c+v-2];v-=1; for e in range(1,len(y)-2): if (y[e-1]<y[e]>y[e+1])or((y[e-1]<y[e]==y[e+1])and(y[e]>y[e+2])): maxy.append(e);minmaxy.append(e);cy+=1; if (y[e-1]>y[e]<y[e+1])or((y[e-1]>y[e]==y[e+1])and(y[e]<=y[e+2])): miny.append(e);minmaxy.append(e);vy+=1; if (len(maxy)>1)and(minmaxy[cy+vy-2]==maxy[cy-2])and(minmaxy[cy+vy-1]==maxy[cy-1]): del maxy[cy-2];del minmaxy[cy+vy-2];cy-=1; if (len(miny)>1)and(minmaxy[cy+vy-2]==miny[vy-2])and(minmaxy[cy+vy-1]==miny[vy-1]): del miny[vy-2];del minmaxy[cy+vy-2];vy-=1; return maxx,maxy,minx,miny,pikx,piky,minmaxx,minmaxy;
Метод Dynamic Time Warping для точного соотношения вершин 1 функции вероятности с вершинами 2 функции вероятности:
import numpy import numpy as np from numpy.fft import fft, fftfreq import matplotlib.pyplot as plt from numpy import linspace, loadtxt, ones, convolve from numpy import array, zeros, argmin, inf from numpy.linalg import norm def _trackeback(D): i, j = array(D.shape) - 1 p, q = [i], [j] while (i > 0 and j > 0): tb = argmin((D[i-1, j-1], D[i-1, j], D[i, j-1])) if (tb == 0): i = i - 1 j = j - 1 elif (tb == 1): i = i - 1 elif (tb == 2): j = j - 1 p.insert(0, i) q.insert(0, j) p.insert(0, 0) q.insert(0, 0) return (array(p), array(q)) def dtw(dr): r, c = len(dr), len(dr[0]); D = zeros((r + 1, c + 1)); D[0, 1:] = inf D[1:, 0] = inf for i in range(r): for j in range(c): D[i+1, j+1] = dr[i][j]; for i in range(r): for j in range(c): D[i+1, j+1] += min(D[i, j], D[i, j+1], D[i+1, j]) D = D[1:, 1:]; dist = D[-1, -1] / sum(D.shape); return dist, D, _trackeback(D)
Теперь применим метод DTW для поиска соответствия вершин одной кривой к другой и если найдена лишняя вершина у одной из функций записываем в вершину пологую точку на кривой с тем же отступом, как будто бы у нас на самом деле там критическая точка.
def pikmatch(x,y,maxx,maxy,optimal,minmaxx,miny,minx): uj=0;pikk=[[float("inf") for m in range(len(maxy))] for t in range(len(maxx))];pi=[0 for m in range(len(maxx))];ret=1;p=[];nad=0;wax=[];way=[];re=1; for e in range(len(maxx)): for l in range(len(maxy)): pikk[e][l]=(((abs(x[maxx[e]]-y[maxy[l]])+0.001)**1)*(abs(maxx[e]-maxy[l]+optimal)+1)); pi[e]=min(pikk[e]);p.append(pikk[e].index(min(pikk[e])));p[e]=maxy[p[e]];nad=nad+pi[e]; if len(minx)==0: minx=[];minx.append(1) if len(miny)==0: miny=[];miny.append(1) dob=1;res=0;pikk1=[[float("inf") for m in range(len(miny))] for t in range(len(minx))];p1=[];pi1=[0 for m in range(len(minx))]; for e in range(len(minx)): for l in range(len(miny)): pikk1[e][l]=(((abs(x[minx[e]]-y[miny[l]])+0.001)**1)*(abs(minx[e]-miny[l]-optimal)+1)); pi1[e]=min(pikk1[e]);p1.append(pikk1[e].index(min(pikk1[e])));p1[e]=miny[p1[e]];nad=nad+pi1[e]; dt1=dtw(pikk);dt=dt1[2];dt2=dtw(pikk1);dt3=dt2[2]; for v in range(len(dt[1])): p[dt[0][v]]=maxy[dt[1][v]];pi[dt[0][v]]=pikk[dt[0][v]][dt[1][v]]; if (v>0)and(dt[0][v]==dt[0][v-1])and(pikk[dt[0][v-1]][dt[1][v-1]]<pi[dt[0][v]]): p[dt[0][v]]=maxy[dt[1][v-1]];pi[dt[0][v]]=pikk[dt[0][v-1]][dt[1][v-1]]; for v in range(len(dt3[1])): p1[dt3[0][v]]=miny[dt3[1][v]];pi1[dt3[0][v]]=pikk1[dt3[0][v]][dt3[1][v]]; if (v>0)and(dt3[0][v]==dt3[0][v-1])and(pikk1[dt3[0][v-1]][dt3[1][v-1]]<pi1[dt3[0][v]]): p1[dt3[0][v]]=miny[dt3[1][v-1]];pi1[dt3[0][v]]=pikk1[dt3[0][v-1]][dt3[1][v-1]]; nm=p[:];nm1=p1[:];rmu=1;pp=p;pp1=p1; D = defaultdict(list);D1 = defaultdict(list); for i,item in enumerate(p): D[item].append(i) for i,item in enumerate(p1): D1[item].append(i) D = {k:v for k,v in D.items() if len(v)>1};D1 = {k:v for k,v in D1.items() if len(v)>1} for v in range(len(D.keys())): mah=inf; for e in range(len(D[D.keys()[v]])): mah=pi[D[D.keys()[v]][e]] if pi[D[D.keys()[v]][e]]<mah else mah k=pi.index(mah); if (minmaxx.index(maxx[k])+1)<len(minmaxx): perem=minx.index(minmaxx[minmaxx.index(maxx[k])+1]) if (minmaxx.index(maxx[k])-1)>-1: perem1=minx.index(minmaxx[minmaxx.index(maxx[k])-1]) for e in range(len(D[D.keys()[v]])): if D[D.keys()[v]][e]!=k: ms=D[D.keys()[v]][e];p[ms]=p[k]-(maxx[k]-maxx[ms]); if ((maxx[k]-maxx[ms])<0)and(pp1.count(pp1[perem])==1): p1[perem]=p[ms]-(maxx[ms]-minx[perem]); if ((maxx[k]-maxx[ms])>0)and(pp1.count(pp1[perem1])==1): p1[perem1]=p[ms]-(maxx[ms]-minx[perem1]); for v in range(len(D1.keys())): mah=inf; for e in range(len(D1[D1.keys()[v]])): mah=pi1[D1[D1.keys()[v]][e]] if pi1[D1[D1.keys()[v]][e]]<mah else mah k=pi1.index(mah);#print minmaxx,minx,maxx,(minmaxx.index(minx[k])+1),maxx.index(minmaxx[minmaxx.index(minx[k])+1]) if (minmaxx.index(minx[k])+1)<len(minmaxx): perem=maxx.index(minmaxx[minmaxx.index(minx[k])+1]) if (minmaxx.index(minx[k])-1)>-1: perem1=maxx.index(minmaxx[minmaxx.index(minx[k])-1]) for e in range(len(D1[D1.keys()[v]])): if D1[D1.keys()[v]][e]!=k: ms=D1[D1.keys()[v]][e];p1[ms]=p1[k]-(minx[k]-minx[ms]); if ((minx[k]-minx[ms])<0)and(pp.count(pp[perem])==1): p[perem]=p[ms]-(minx[ms]-maxx[perem]); if ((minx[k]-minx[ms])>0)and(pp.count(pp[perem1])==1): p[perem1]=p[ms]-(minx[ms]-maxx[perem1]); for i in range(len(p1)): if p1[i]>59: p1[i]=59; if p1[i]<0: p1[i]=0; for i in range(len(p)): if p[i]>59: p[i]=59; if p[i]<0: p[i]=0;
Заключительная часть кода, где выполняется выравнивание и сравнение 1440 подряд картинок для поиска звездного года. Он найден в +368 минут как и указано в справочнике звездный год = 365.2564 суток
0.2564*1440 минут в сутках = 369.216
1440-1072=368 минут добавляется к году
Так как в python отсчет идет от 0 элемента, то звездные сутки считаются от -3 минут (+1436 минута) от 1440 (+1440 начало нового периода), а звездный год от 1440-1072 минуты.
def stat_distanc(counter): koeff=60;ex=20;ko=60;b=[0 for e in range(ko+ex)];bb=[0 for e in range(ko+ex)];#C:\\28-08-2004.txt /usr/local/28-08-2004.txt matrix = [line.strip() for line in open('/users/andrejeremcuk/downloads/0505.txt')]; #days.dat matri = [line.strip() for line in open('/users/andrejeremcuk/downloads/0506.txt')]; #days.dat arra=[[ 0 for e in range(koeff)] for t in range(int(len(matrix)/koeff))];harra=[0 for t in range(int(len(matrix)/koeff))]; arrab=[[ 0 for e in range(koeff)] for t in range(int(len(matrix)/koeff))];harrab=[0 for t in range(int(len(matrix)/koeff))];z=0;resume=1;resum=0; arr=[[ 0 for e in range(koeff)] for t in range(int(len(matri)/koeff))]; for i in range(len(matrix)): matrix[i]=int(matrix[i]);matri[i]=int(matri[i]); for jk in range(2880): #int(len(matrix)/koeff) for mk in range(koeff): arra[jk][mk]=matrix[z];arr[jk][mk]=matri[z];z=z+1; for jk in range(2880): harra[jk]=np.histogram(arra[jk], bins=ko, density=False);harrab[jk]=np.histogram(arr[jk], bins=ko, density=False);harra[jk]=harra[jk][0];harrab[jk]=harrab[jk][0] for u in range(5): harra[jk] = movingaverage(harra[jk], 4);harrab[jk]=movingaverage(harrab[jk], 4); for mk in range(1440):# 24000 mi=[];mis=[];mis1=[];mii=[];ei=[];ti=[];dots=[];dots1=[]; if counter=='l': rn=random.randint(0,1439);x=harra[mk];y=harrab[random.randint(0,1439)];#print rn; #y=harra[random.randint(0,1439)]; elif counter=='o': x=harra[summ[mk]-1];y=harra[sum1[mk]-1]; else: x=harra[mk+1440-counter];y=harrab[mk]; x=x.tolist();y=y.tolist(); for kl in range(ko): b[kl+ex/2]=y[kl]; for m in range(ex): ct=[0 for e in range(ko+ex)]; for l in range(ko): ct[l+m]=x[l]; mis.append(euclid(ct,b));mis1.append(euclid(ct[::-1],b)); optimal=mis.index(min(mis))-ex/2;ret=pik(x,y);minmaxx=ret[6];minmaxy=ret[7];maxx=ret[0];maxy=ret[1];minx=ret[2];miny=ret[3] optimal1=mis1.index(min(mis1))-ex/2;#print mk; for k in range(len(minmaxx)): dots.append(x[minmaxx[k]]);#minmaxx[k]=59-minmaxx[k]; for k in range(len(minmaxy)): dots1.append(y[minmaxy[k]]);#minmaxy[k]=59-minmaxy[k] outputs=pikmatch(x,y,maxx,maxy,-optimal,minmaxx,miny,minx); outputs1=pikmatch(y,x,maxy,maxx,optimal,minmaxy,minx,miny); plt.plot(minmaxx,dots,'go', alpha=0.5, ms=10);plt.plot(minmaxy,dots1,'bo', alpha=0.5, ms=10); plt.plot(y,linewidth=4, alpha=0.5);plt.plot(x,linewidth=4, alpha=0.5);#plt.show(); mx1=minmaxx[:];my1=minmaxy[:];mxx1=maxx[:];mxx2=minx[:] for k in range(len(minmaxx)): dots.append(x[minmaxx[k]]);minmaxx[k]=59-minmaxx[k]; for k in range(len(maxx)): maxx[k]=59-maxx[k]; for k in range(len(minx)): minx[k]=59-minx[k]; minmaxx=minmaxx[::-1];maxx=maxx[::-1];minx=minx[::-1]; output=pikmatch(x[::-1],y,maxx,maxy,-optimal1,minmaxx,miny,minx);minmaxx=minmaxx[::-1];mx2=minmaxx[:]; # for k in range(len(minmaxy)): dots1.append(y[minmaxy[k]]);#minmaxy[k]=59-minmaxy[k] minmaxx=mx1[:]; output1=pikmatch(y,x[::-1],maxy,maxx,optimal1,minmaxy,minx,miny); resume+=min(outputs1[1]+outputs[1],output[1]+output1[1]); #minmaxx=mx2[:];plt.plot(minmaxx,dots,'go');plt.plot(my1,dots1,'bo');plt.plot(y);plt.plot(x[::-1]);plt.show(); #plt.plot(x); return resume/10000; stat_distanc('o') stat_distanc(1072)
Примеры похожих картинок:

Несмотря на то что эффект Шноля заявляет о нахождении солнечных суток и солнечного года, таких периодов не было обнаружено.
Звездные сутки были обнаружены в окрестностях +1440 — i минут +1436 минута:
199.892665349 -10 i 203.488567732 -9 i 209.135017031 -8 196.712944345 -7 201.306389699 -6 209.494707844 -5 213.761404735 -4 220.989501281 -3 214.488889148 -2 207.859987762 -1 221.399812849 0 208.188622006 1 202.261474872 2 195.414598182 3 период! 203.675784045 4 210.319165323 5 210.090229703 6 223.712227452 7 231.477304378 8 204.582579082 9
Звездный год — было подсчитаны все сутки от 365 до 366 суток нового года:
bas=[]; for i in range(1440): bas.append(stat_distanc(i));print i; min(bas) - 1072
1440-1072, 368 то есть +369 дополнительная минута нового года. Точно звездный год 365 дней и 369 минута [365.2564]! (надо учитывать что отсчет начинается с 0 минуты)
Для тех кто решит все сам проверить и возможно улучшить распознавание образов весь код и данные доступны на Github
Спасибо за внимание!
