How to become an author
Search
Write a publication
Pull to refresh

Обзор градиентных методов в задачах математической оптимизации

Reading time11 min
Views108K
Mathematics*Machine learning*
From sandbox

Предисловие


В этой статье речь пойдет о методах решения задач математической оптимизации, основанных на использовании градиента функции. Основная цель — собрать в статье все наиболее важные идеи, которые так или иначе связаны с этим методом и его всевозможными модификациями.





UPD. В комментариях пишут, что на некоторых браузерах и в мобильном приложении формулы не отображаются. К сожалению, не знаю, как с этим бороться. Могу лишь сказать, что использовал макросы «inline» и «display» хабравского редактора. Если вдруг знаете, как это исправить — напишите в комментариях, пожалуйста.

Примечание от автора


На момент написания я защитил диссертацию, задача которой требовала от меня глубокое понимание теоретических основно методов математической оптимизации. Тем не менее, у меня до сих пор (как и у всех) расплываются глаза от страшных длинных формул, поэтому я потратил немалое время, чтобы вычленить ключевые идеи, которые бы характеризовали разные вариации градиентных методов. Моя личная цель — написать статью, содержащую минимальное количество информации, необходимое для более менее подробного понимания тематики. Но будьте готовы, без формул так или иначе не обойтись.

Постановка задачи


Прежде чем описывать метод, следует сначала описать задачу, а именно: «Даны множество $\mathcal{K}$ и функция $f:\mathcal{K}\rightarrow \mathbb{R}$, требуется найти точку $x^*\in \mathcal{K}$, такую что $ f(x)\geq f(x^*)$ для всех $x\in \mathcal{K}$», что обычно записывается например вот так

$f(x)\rightarrow \min_{x\in \mathcal{K}}.$


В теории обычно предполагается, что $f$ — дифференцируемая и выпуклая функция, а $\mathcal{K}$ — выпуклое множество (а еще лучше, если вообще $\mathcal{K}=\mathbb{R}^n$), это позволяет дать какие-то гарантии успешности применения градиентного спуска. На практике градиентный спуск успешно применяется даже когда у задачи нет ни одного из вышеперечисленных свойств (пример дальше в статье).

Немного математики


Допустим пока что нам нужно просто найти минимум одномерной функции

$f(x)\rightarrow \min_{x\in \mathbb{R}}.$


Еще в 17 веке Пьером Ферма был придуман критерий, который позволял решать простые задачи оптимизации, а именно, еcли $x^* $ — точка минимума $f^* $, то

$f'(x^*)=0 $


где $f'$ — производная $f$. Этот критерий основан на линейном приближении

$ f(x)\approx f(x^*)+f'(x^*)(x-x^*).$


Чем ближе $x$ к $x^*$, чем точнее это приближение. В правой части — выражение, которое при $f'(x^*)\neq 0$ может быть как больше $f(x^*)$ так и меньше — это основная суть критерия. В многомерном случае аналогично из линейного приближения $f(x)\approx f(x^*)+\nabla f(x^*)^T(x-x^*)$ (здесь и далее $x^Ty=\sum_{i=1}^nx_iy_i$ — стандартное скалярное произведение, форма записи обусловлена тем, что скалярное произведение — это то же самое, что матричное произведение вектор-строки на вектор-столбец) получается критерий

$\nabla f(x^*)=0. $


Величина $\nabla f(x^*)$ — градиент функции $f$ в точке $x^*$. Также равенство градиента нулю означает равенство всех частных производных нулю, поэтому в многомерном случае можно получить этот критерий просто последовательно применив одномерный критерий по каждой переменной в отдельности.

Стоит отметить, что указанные условия являются необходимыми, но не достаточными, самый простой пример — 0 для $f(x)=x^2$ и $f(x)=x^3$


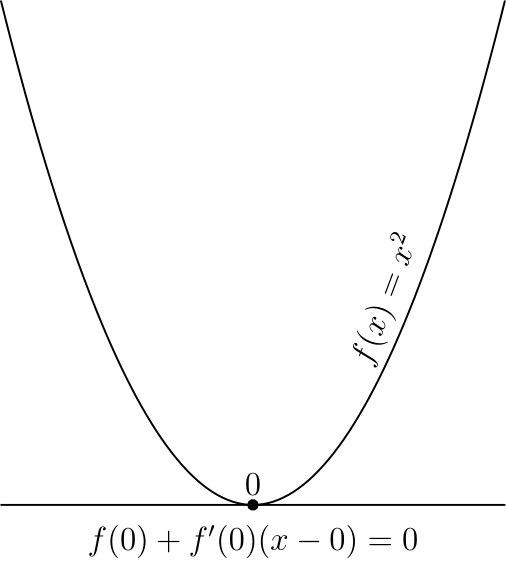
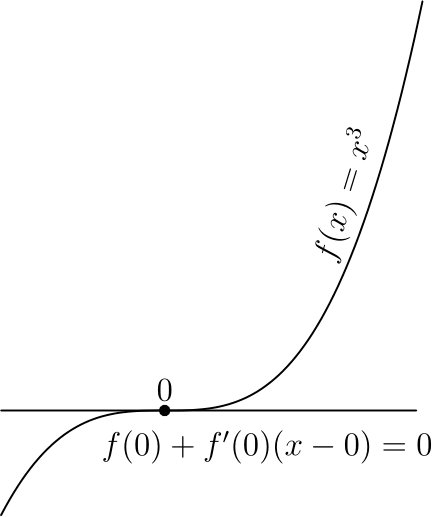
Этот критерий является достаточным в случае выпуклой функции, во многом из-за этого для выпуклых функций удалось получить так много результатов.

Квадратичные функции


Квадратичные функции в $\mathbb{R}^n$ — это функция вида

$ f(x) = f(x_1, x_2, \ldots, x_n)=\frac{1}{2}\sum_{i,j=1}^na_{ij}x_ix_j-\sum_{i=1}^n b_ix_i+c $


Для экономии места (да и чтобы меньше возиться с индексами) такую функцию обычно записывают в матричной форме:

$ f(x) = \frac{1}{2}x^TAx-b^Tx+c, $


где $x=(x_1, \ldots, x_n)^T$, $b=(b_1, \ldots, b_n)^T$, $A$ — матрица, у которой на пересечении $i$ строки и $j$ столбца стоит величина
$\frac{1}{2}(a_{ij}+a_{ji})$ ($A$ при этом получается симметричной — это важно). Далее. при упомянании квадратичной функции я буду иметь указанную выше функцию.

Зачем я об этом рассказываю? Дело в том, что квадратичные функции важны в оптимизации по двум причинам:

  1. Они тоже встречаются на практике, например при построении линейной регрессии методом наименьших квадратов
  2. Градиент квадратичной функции — линейная функция, в частности для функции выше

    $ \frac{\partial}{\partial x_i} f(x_1, x_2, \ldots, x_n) = a_{ii} x_i + \sum_{j\neq i}\frac{1}{2}(a_{ij}+a_{ji})x_j -b_i, $


    Или в матричной форме

    $ \nabla f(x) = Ax-b, $


    Таким образом система $\nabla f(x)=0$ — линейная система. Системы, проще чем линейная, просто не существует. Мысль, к которой я старался подобраться — оптимизация квадратичной функции — самый простой класс задач оптимизации. С другой стороны, тот факт, что $\nabla f(x^*)=0$ — необходимые условия минимума дает возможность решать линейные системы через задачи оптимизации. Чуть позже я постараюсь вас убедить в том, что это имеет смысл.

Полезные свойства градиента


Хорошо, мы вроде бы выяснили, что если функция дифференцируема (у нее существуют производные по всем переменным), то в точке минимума градиент должен быть равен нулю. А вот несет ли градиент какую-нибудь полезную информацию в случае, когда он отличен от нуля?

Попробуем пока решить более простую задачу: дана точка $x$, найти точку $\bar{x}$ такую, что $f(\bar{x})<f(x)$. Давайте возьмем точку рядом с $x$, опять же используя линейное приближение $f(\bar{x})\approx f(x)+\nabla f(x)^T(\bar{x}-x)$. Если взять $\bar{x}=x-\alpha\nabla f(x)$, $ \alpha>0$ то мы получим

$ f(\bar{x})\approx f(x)-\alpha\|\nabla f(x)\|^2<f(x). $


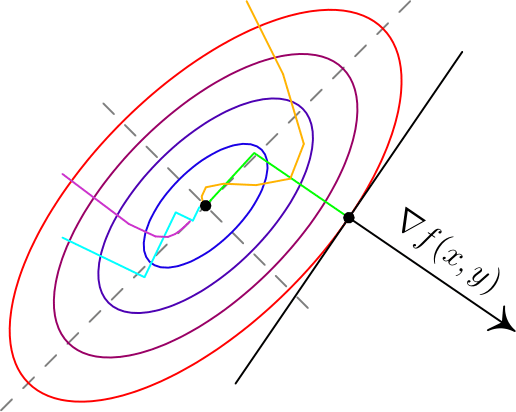
Аналогично, если $ \alpha<0 $, то $f(\bar{x})$ будет больше $f(x)$ (здесь и далее $||x||=\sqrt{x_1^2+x_2^2+\ldots+x_n^2}~$). Опять же, так как мы использовали приближение, то эти соображения будут верны только для малых $\alpha$. Подытоживая вышесказанное, если $\nabla f(x)\neq 0$, то градиент указывает направление наибольшего локального увеличения функции.

Вот два примера для двумерных функций. Такого рода картинки можно часто увидеть в демонстрациях градиентного спуска. Цветные линии — так называемые линии уровня, это множество точек, для которых функция принимает фиксированное значений, в моем случае это круги и эллипсы. Я обозначил синими линии уровня с более низким значением, красными — с более высоким.



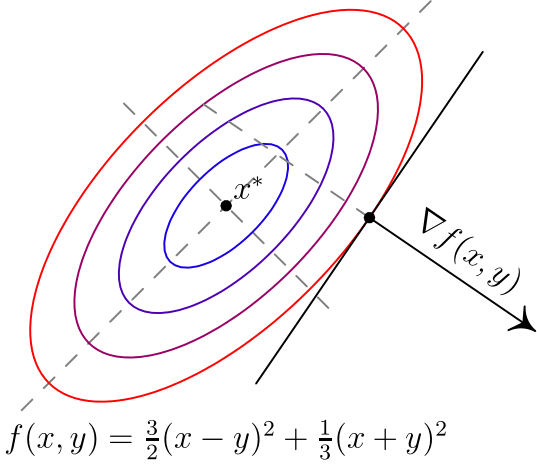
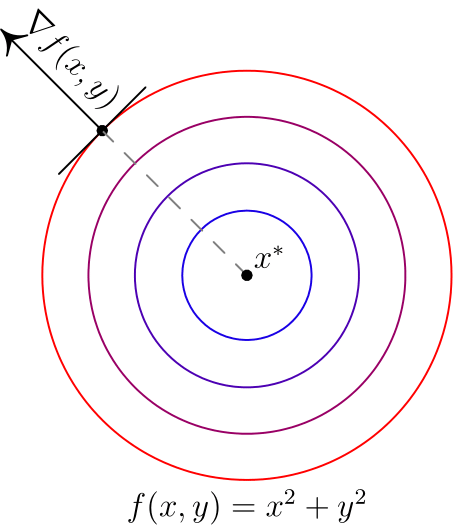
Обратите внимание, что для поверхности, заданной уравнением вида $f(x)=c$, $\nabla f(x) $ задает нормаль (в простонародии — перпендикуляр) к этой поверхности. Также обратите внимание, что хоть градиент и показывает в направлении наибольшего увеличения функции, нет никакой гарантии, что по направлению, обратному к градиенту, можно найти минимум (пример — левая картинка).

Градиентный спуск


До базового метода градиентного спуска остался лишь малый шажок: мы научились по точке $x$ получать точку $\bar{x}$ с меньшим значением функции $ f$. Что мешает нам повторить это несколько раз? По сути, это и есть градиентный спуск: строим последовательность

$ x_{k+1}=x_k-\alpha_k\nabla f(x_k). $


Величина $\alpha_k$ называется размером шага (в машинном обучении — скорость обучения). Пару слов по поводу выбора $\alpha_k$: если $\alpha_k$ — очень маленькие, то последовательность медленно меняется, что делает алгоритм не очень эффективным; если же $\alpha_k$ очень большие, то линейное приближение становится плохим, а может даже и неверным. На практике размер шага часта подбирают эмпирически, в теории обычно предполагается липшицевость градиента, а именно, если

$ \|\nabla f(x)-\nabla f(y)\|\leq L\|x-y\| $


для всех $x,y$, то $\alpha_k< \frac{2}{L}$ гарантирует убывание $f(x_k)$.

Анализ для квадратичных функций


Если $A$ — симметричная обратимая матрица, $Ax^*=b$, то для квадратичной функции $f(x)=\frac{1}{2}x^TAx-b^Tx+c$ точка $x^*$ является точкой минимума (UPD. при условии, что этот минимум вообще существует — $f$ не принимает сколько угодно близкие к $-\infty$ значения только если $A$ положительно определена), а для метода градиентного спуска можно получить следующее

$ x_{k+1}-x^* = x_k-\alpha_k \nabla f(x_k)-x^* = x_k-\alpha_k(Ax_k-b)-x^*= $


$ (x_k-x^*)-\alpha_kA(x_k-x^*)=(I-\alpha_k A)(x_k-x^*), $


где $ I $ — единичная матрица, т.е. $ Ix=x$ для всех $ x$. Если же $\alpha_k\equiv\alpha$, то получится

$ \|x_{k}-x^*\|=\|(I-\alpha A)^k(x_0-x^*)\|\leq \|I-\alpha A\|^k \|x_0-x^*\|. $


Выражение слева — расстояние от приближения, полученного на шаге $k$ градиентного спуска до точки минимума, справа — выражение вида $\lambda^k \beta$, которое сходится к нулю, если $|\lambda|<1$ (условие, которое я писал на $\alpha$ в предыдущем пункте как раз это гарантирует). Эта базовая оценка гарантирует, что градиентный спуск сходится.

Модификации градиентного спуска


Теперь хотелось бы рассказать немного про часто используемые модификации градиентного спуска, в первую очередь так называемые

Инерционные или ускоренные градиентные методы


Все методы такого класса выражаются в следующем виде

$ x_{k+1}=x_k-\alpha_k\nabla f(x_k)+\beta_k(x_k-x_{k-1}). $


Последнее слагаемое характеризует эту самую «инерционность», алгоритм на каждом шаге старается двигаться против градиента, но при этом по инерции частично двигается в том же направлении, что и на предыдущей итерации. Такие методы обладают двумя важными свойствами:

  1. Они практически не усложняют обычный градиентный спуск в вычислительном плане.
  2. При аккуратном подборе $\alpha_k, \beta_k$ такие методы на порядок быстрее, чем обычный градиентный спуск даже с оптимально подобранным шагом.

Один из первых таких методов появился в середине 20 века и назывался метод тяжелого шарика, что передавало природу инерционности метода: в этом методе $\alpha_k, \beta_k$ не зависят от $k$ и аккуратно подбираются в зависимости от целевой функции. Стоит отметить, что $\alpha_k$ может быть какой угодно, а $\beta_k$ — обычно лишь чуть-чуть меньше единицы.

Метод тяжелого шарика — самый простой инерционный метод, но не самый первый. При этом, на мой взгляд, самый первый метод довольно важен для понимания сути этих методов.

Метод Чебышева


Да да, первый метод такого типа был придуман еще Чебышевым для решения систем линейных уравнений. В какой-то момент при анализе градиентного спуска было получено следующее равенство

$ x_{k+1}-x^* = (I-\alpha_k A) (x_k-x^*)=\ldots= $


$ (I-\alpha_kA)(I-\alpha_{k-1}A)\ldots(I-\alpha_1A)(x_0-x^*)=P_k(A)(x_0-x^*), $


где $P_k$ — некоторый многочлен степени $k$. Почему бы не попробовать подобрать $\alpha_k$ таким образом, чтобы $P_k(A)(x_0-x^*)$ было поменьше? Один уз универсальных многочленов, которые меньше всего отклоняются от нуля — многочлен Чебышева. Метод Чебышева по сути заключается в том, чтобы подобрать параметры спуска так, чтобы $P_k$ был многочленом Чебышева. Есть правда одна небольшая проблема: для обычного градиентного спуска это просто невозможно. Однако для инерционных методов это оказывается возможным. В основном это происходит из-за того, что многочлены Чебышева удовлетворяют рекуррентному соотношению второго порядка

$ T_{n+1}(x)=2xT_n(x)-T_{n-1}(x), $


поэтому их невозможно построить для градиентного спуска, который вычисляет новое значение лишь по одному предыдущему, а для инерционных становится возможным за счет того, что используется два предыдущих значения. При этом оказывается, что сложность вычисления $\alpha_k,\beta_k$ не зависит ни от $k$, ни от размера пространства $n$.

Метод сопряженных градиентов


Еще один очень интересный и важный факт (следствие теоремы Гамильтона-Кэли): для любой квадратной матрицы $A$ размера $n\times n$ существует многочлен $P$ степени не больше $n$, для которого $P(A)=0$. Чем это интересно? Все дело в том же равенстве

$ x_{k+1}-x^* = P_k(A)(x_0-x^*). $


Если бы мы могли подбирать размер шага в градиентном спуске так, чтобы получать именно этот обнуляющий многочлен, то градиентный спуск сходился бы за фиксированное число итерации не большее размерности $A$. Как уже выяснили — для градиентного спуска мы так делать не можем. К счастью, для инерционных методов — можем. Описание и обоснование метода довольно техническое, я ограничусь сутью:на каждой итерации выбираются параметры, дающие наилучший многочлен, который можно построить учитывая все сделанные до текущего шага измерения градиента. При этом

  1. Одна итерация градиентного спуска (без учета вычислений параметров) содежит одно умножение матрицы на вектор и 2-3 сложения векторов
  2. Вычисление параметров также требует 1-2 умножение матрицы на вектор, 2-3 скалярных умножения вектор на вектор и несколько сложений векторов.

Самое сложное в вычислительном плане — умножение Матрицы на вектор, обычно это делается за время $\mathcal{O}(n^2)$, однако для со специальной реализацией это можно сделать за $\mathcal{O}(m) $, где $m$ — количество ненулевых элементов в $A$. Учитывая сходимость метода сопряженных градиентов не более, чем за $n$ итерации получаем общую сложность алгоритма $\mathcal{O}(nm)$, что во всех случаях не хуже $\mathcal{O}(n^3)$ для метода Гаусса или Холесского, но намного лучше в случае, если $m<<n^2$, что не так редко встречается.

Метод сопряженных градиентов хорошо работает и в случае, если $f$ не является квадратичной функцией, но при этом уже не сходится за конечное число шагов и часто требует небольших дополнительных модификаций

Метод Нестерова


Для сообществ математической оптимизации и машинного обучения фамилия «Нестеров» уже давно стало нарицательной. В 80х годах прошлого века Ю.Е. Нестеров придумал интересный вариант инерционного метода, который имеет вид

$ x_{k+1}=x_k-\alpha_k\nabla f(x_k+\beta_k(x_k-x_{k-1}))+\beta_k(x_k-x_{k-1}), $


при этом не предполагается какого-то сложного подсчета $\alpha_k,\beta_k$ как в методе сопряженных градиентов, в целом поведение метода похоже на метод тяжелого шарика, но при этом его сходимость обычно гораздо надежнее как в теории, так и на практике.

Стохастический градиентный спуск


Единственное формальное отличие от обычного градиентного спуска — использование вместо градиента функции $g(x, \theta)$ такой, что $E_\theta g(x,\theta)=\nabla f(x)$ ($E_\theta$ — математическое ожидание по случайной величине $\theta$), таким образом стохастический градиентный спуск имеет вид

$ x_{k+1}=x_k-\alpha_kg(x_k, \theta_k). $


$\theta_k$ — это некоторый случайный параметр, на который мы не влияем, но при этом в среднем мы идем против градиента. В качестве примера рассмотрим функции

$ f(x)=\frac{1}{2m}\sum_{j=1}^m\|x-y_j\|^2,~~\nabla f(x)=\frac{1}{m}\sum_{j=1}^m(x-y_j) $


и

$ g(x, i)=x-y_i. $


Если $i$ принимает значения $1,\ldots, m$ равновероятно, то как раз в среднем $g$ — это градиент $f$. Этот пример показателен еще и следующим: сложность вычисления градиента в $m$ раз больше, чем сложность вычисления $g$. Это позволяет стохастическому градиентному спуску делать за одно и то же время в $m$ раз больше итераций. Несмотря на то, что стохастический градиентный спуск обычно сходится медленней обычного, за счет такого большого увеличения числа итераций получается улучшить скорость сходимости на единицу времени. Насколько мне известно — на данный момент стохастический градиентный спуск является базовым методом обучения большинства нейронных сетей, реализован во всех основных библиотеках по ML: tensorflow, torch, caffe, CNTK, и т.д.

Стоит отметить, что идеи иннерционных методов применяются для стохастического градиентного спуска и на практике часто дают прирост, в теории же обычно считается, что асимптотическая скорость сходимости не меняется из-за того, что основная погрешность в стохастическом градиентном спуске обусловлена дисперсией $g$.

Субградиентный спуск


Эта вариация позволяет работать с недифференцируемыми функциями, её я опишу более подробно. Придется опять вспомнить линейное приближение — дело в том, что есть простая характеристика выпуклости через градиент, дифференцируемая функция $f$ выпукла тогда и только тогда, когда выполняется $f(y)\geq f(x)+\nabla f(x)^T(y-x)$ для всех $x, y$ . Оказывается, что выпуклая функция не обязаны быть дифференцируемой, но для любой точки $x$ обязательно найдется такой вектор $g$, что $f(y)\geq f(x)+g^T(y-x)$ для всех $y$. Такой вектор $g$ принято называть субградиентом $f$ в точке $x$, множество всех субградиентов в точки $x$ называют субдифференциалом $x$ и обозначают $\partial f(x)$ (несмотря на обозначение — не имеет ничего общего с частными производными). В одномерном случае $g$ — это число, а вышеуказанное свойство просто означает, что график $f$ лежит выше прямой, проходящей через $(x, f(x))$ и имеющей тангенс угла наклона $g$ (смотрите рисунки ниже). Отмечу, что субградиентов для одной точки может быть несколько, даже бесконечное число.



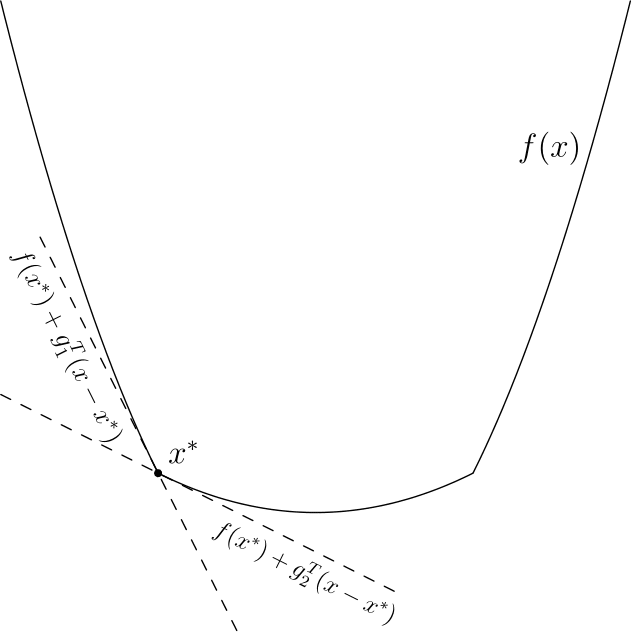
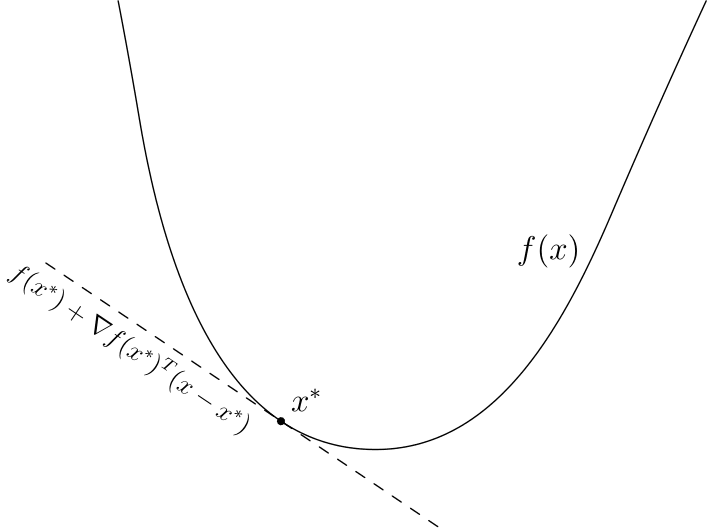
Вычислить хотя бы один субградиент для точки обычно не очень сложно, субградиентный спуск по сути использует субградиент вместо градиента. Оказывается — этого достаточно, в теории скорость сходимости при этом падает, однако например в нейронных сетях недифференцируемую функцию $ReLU(x)=\max(0, x)$ любят использовать как раз из-за того, что с ней обучение проходит быстрее (это кстати пример невыпуклой недифференцируемой функции, в которой успешно применяется (суб)градиентный спуск. Сама по себе функция $ReLU$ выпукла, но многослойная нейронная сеть, содержащая $ReLU$, невыпукла и недифференцируема). В качестве примера, для функции $f(x)=|x|$ субдифференциал вычисляется очень просто

$ \partial f(x)=\begin{cases} 1, & x>0, \\ -1, & x < 0, \\ [-1, 1], & x=0. \end{cases} $



Пожалуй, последняя важная вещь, которую стоит знать, — это то, что субградиентный спуск не сходится при постоянном размере шага. Это проще всего увидеть для указанной выше функции $f(x)=|x|$. Даже отсутствие производной в одной точке ломает сходимость:

  1. Допустим мы начали из точки $x_0$.
  2. Шаг субградиентного спуска:

    $ x_{k+1}=\begin{cases} x_{k}-1, & x>0, \\ x_k+1, & x < 0, \\ ??? & x=0. \end{cases} $

  3. Если $x_0>0$, то первые несколько шагов мы будет вычитать единицу, если $x_0<0$, то прибавлять. Так или иначе мы в какой-то момент окажемся на интервале $[0, 1)$, из которого попадем в $[-1, 0)$, а дальше будем прыгать между двумя точками этих интервалов.

В теории для субградиентного спуска рекомендуется брать последовательность шагов

$ \alpha_k=\frac{1}{(k+1)^c}. $


Где $c$ обычно $1$ или $\frac{1}{2}$. На практике я часто видел успешное применение шагов $\alpha_k=e^{-ck}$, хоть и для таких шагов вообще говоря не будет сходимости.

Proximal методы


К сожалению я не знаю хорошего перевода для «proximal» в контексте оптимизации, поэтому просто так и буду называть этот метод. Proximal-методы появились как обобщение проективных градиентных методов. Идея очень простая: если есть функция $f$, представимая в виде суммы $f(x)=\varphi(x)+h(x)$, где $\varphi$ — дифференцируемая выпуклая функция, а $h(x)$ — выпуклая, для которой существует специальный proximal-оператор $prox_h(x)$ (в этой статье ограничусь лишь примерами, описывать в общем виде не буду), то свойства сходимости градиентного спуска для $\varphi$ остаются и для градиентного спуска для $f$, если после каждой итерации применять этот proximal-оператор для текущей точки $x_k$, другими словами общий вид proximal-метода выглядит так:

$ x_{k+1}=prox_{\alpha_kh}(x_k-\alpha_k\nabla \varphi(x_k)) $


Думаю, пока что совершенно непонятно, зачем это может понадобиться, особенно учитывая то, что я не объяснил, что такое proximal-оператор. Вот два примера:
  1. $h(x)$ — индикатор-функция выпуклого множества $\mathcal{K}$, то есть

    $ h(x)=\begin{cases} 0, & x\in \mathcal{K},\\ +\infty, & x\notin \mathcal{K}.\\ \end{cases} $


    В этом случае $prox_{\alpha_kh}(x)$ — это проекция на множество $\mathcal{K}$, то есть «ближайшая к $x$ точка множества $\mathcal{K}$». Таким образом, мы ограничиваем градиентный спуск только на множество $\mathcal{K}$, что позволяет решать задачи с ограничениями. К сожалению, вычисление проекции в общем случае может быть еще более сложной задачей, поэтому обычно такой метод применяется, если ограничения имеют простой вид, например так называемые box-ограничения: по каждой координате

    $ l_i\leq x_i\leq r_i $


  2. $h(x)=\lambda \|x\|_1=\lambda\sum_{i=1}^n|x_i|$ — $\ell_1$-регуляризация. Такое слагаемое любят добавлять в задачи оптимизации в машинном обучении, чтобы избежать переобучения. Регуляризация такого вида еще и имеет тенденцию обнулять наименее значимые компоненты. Для такой функции proximal-оператор имеет вид (ниже описано выражение для одной координаты):

    $ [prox_{\alpha h}(x)]_i=\begin{cases} x_i-\alpha, & x_i>\alpha,\\ x_i+\alpha, & x_i <-\alpha,\\ 0, & x_i\in [-\alpha, \alpha], \end{cases} $


    что довольно просто вычислить.

Заключение


На этом заканчиваются основные известные мне вариации градиентного метода. Пожалуй под конец я бы отметил, что все указанные модификации (кроме разве что метода сопряженных градиентов) могут легко взаимодействовать друг с другом. Я специально не стал включать в эту перечень метод Ньютона и квазиньютоновские методы (BFGS и прочие): они хоть и используют градиент, но при этом являются более сложными методами, требуют специфических дополнительных вычислений, которые обычно более вычислительно затратны, нежели вычисление градиента. Тем не менее, если этот текст будет востребован, я с удовольствием сделаю подобный обзор и по ним.

Использованная / рекомендованная литература


Boyd. S, Vandenberghe L. Convex Optimization
Shewchuk J. R. An Introduction to the Conjugate Gradient Method Without the Agonizing Pain
Bertsekas D. P. Convex Optimization Theory

Нестеров Ю. Е. Методы выпуклой оптимизации
Гасников А. В. Универсальный градиентный спуск
Tags:
Hubs:
If this publication inspired you and you want to support the author, do not hesitate to click on the button
Total votes 76: ↑76 and ↓0+76
Comments26
71
Karma
0.1
Rating
Николай Мальковский @malkovsky

Математик, программист, пианист

Send message
VK

Articles

Your account

Sections

Information

Services

Support
© 2006–2025, Habr