maisvendoo 10 окт 2018 в 18:35

Принцип наименьшего действия в аналитической механике

10 мин

25K

Туториал

Предыстория

Причина данной публикации — неоднозначная статья на тему принципа наименьшего действия (ПНД), опубликованная на ресурсе несколько дней назад. Неоднозначна она потому, что её автор в популярной форме пытается донести до читателя один из основополагающих принципов математического описания природы, и это частично ему удается. Если бы не одно но, притаившееся в конце публикации. Под спойлером приведена полная цитата данного отрывка

Задача о движении шарика

Не все так просто

На самом деле я немного обманул, сказав, что тела всегда двигаются так, чтобы минимизировать действие. Хотя в очень многих случаях это действительно так, можно придумать ситуации, в которых действие явно не минимально.

Например, возьмем шарик и поместим его в пустое пространство. На некотором отдалении от него поставим упругую стенку. Допустим, мы хотим, чтобы через некоторое время шарик оказался в том же самом месте. При таких заданных условиях шарик может двигаться двумя разными способами. Во-первых, он может просто оставаться на месте. Во-вторых, можно его толкнуть по направлению к стенке. Шарик долетит до стенки, отскочит от нее и вернется обратно. Понятно, что можно толкнуть его с такой скоростью, чтобы он вернулся в точно нужное время.

Оба варианта движения шарика возможны, но действие во втором случае получится больше, потому что все это время шарик будет двигаться с ненулевой кинетической энергией.

Как же спасти принцип наименьшего действия, чтобы он был справедлив и в таких ситуациях? Об этом мы поговорим в следующий раз.

Так в чем же, с моей точки зрения, проблема?

Проблема в том, что автор, приводя данный пример допустил ряд фундаментальных ошибок. Она усугубляется тем, что планируемая вторая часть, со слов автора, будет опираться на эти ошибки. Руководствуясь принципом наполнения ресурса достоверной информацией я вынужден выступить с разъяснением своей позиции по данному вопросу более развернуто, и формат комментариев для этого маловат.

Данная статья расскажет о том, как строится механика на базе ПНД, и постарается объяснить читателю, что проблема, которую ставит автор цитируемой публикации отсутствует.

1. Определение действия по Гамильтону. Принцип наименьшего действия

Действием по Гамильтону называют функционал

$S = \int\limits_{t_1}^{t_2} \, L\left(\mathbf q(t), \dot{\mathbf q}(t) \right) \, dt$

где

$L\left(\mathbf q(t), \dot{\mathbf q}(t) \right) = T\left(\mathbf q(t), \dot{\mathbf q}(t) \right) - \Pi(\mathbf q)$

— функция Лагранжа, для некоторой механической системы, в которой (опуская аргументы в дальнейшем) T — кинетическая энергия системы; П — потенциальная её энергия; q(t) — вектор обобщенных координат этой системы, являющийся функцией времени. при этом полагают, что моменты времени t₁ и t₂ — фиксированы.

Почему функционал, а не функция? Потому, что функция, по определению есть правило, по которому одному числу из области определения (аргументу функции) ставится в соответствие другое число из области значений. Функционал отличается тем, что качестве его аргумента выступает не число, а целая функция. В данном случае это закон движения механической системы q(t), определенный по крайней мере на промежутке времени между t₁ и t₂.

Многолетние (и это мягко сказано!) труды ученых-механиков (включая умопомрачительного Леонарда Эйлера), позволили сформулировать

Принцип наименьшего действия:

Механическая система, для которой задана функция Лагранжа $L\left(\mathbf q(t), \dot{\mathbf q}(t) \right)$ , движется таким образом, что закон её движения q(t) доставляет минимум функционалу

$S = \int\limits_{t_1}^{t_2} \, L\left(\mathbf q(t), \dot{\mathbf q}(t) \right) \, dt \to \min$

называемому действием по Гамильтону.

Уже из самого определения ПНД следует тот факт, что данный принцип приводит к уравнениям движения лишь для ограниченного класса механических систем. Для каких? А давайте разберемся.

2. Границы применимости принципа наименьшего действия. Некоторые определения для самых маленьких

Как следует из определения, опять таки, функции Лагранжа, ПНД позволяет получить уравнения движения для механических систем, силовое воздействие на которые определяется исключительно потенциальной энергией. Для того чтобы разобраться, о каких системах идет речь, дадим несколько определений, которые, для экономии объема статьи я помещаю под спойлер

Работа силы на перемещении

Рассмотрим движущуюся по траектории AB точку, к которой приложена сила $\vec F$ . Бесконечно малое перемещение точки по траектории определяется вектором $d\vec s$ , направленным по касательной к траектории.

Элементарной работой силы $\vec F$ на перемещении $d\vec s$ называют скалярную величину, равную

$dA = \vec F \cdot d\vec s$

Тогда, полная работа силы на перемещении точки по траектории AB есть криволинейный интеграл

$A = \int\limits_{AB} \, \vec F \cdot d\vec s$

Кинетическая энергия точки

Кинетической энергией точки T называют работу, которую должны совершить приложенные к точке массой m силы, для того чтобы из состояния покоя перевести точку в движение со скоростью $\vec v$

Вычислим кинетическую энергию, согласно данному определению. Пусть точка начинает движение из состояния покоя под действием приложенных к ней сил. На отрезке траектории AB она приобретает скорость $\vec v$ . Вычислим работу, совершенную приложенными к точке силами, которые, по принципу независимости действия сил, заменим равнодействующей $\vec F$

$T = A = \int\limits_{AB} \, \vec F \cdot d\vec s$

В соответствии со вторым законом Ньютона

$\vec F = m \, \vec a = m \, \frac{d\vec v}{dt}$

тогда

$T = \int\limits_{AB} \, \vec F \cdot d\vec s = m \, \int\limits_{AB} \frac{d\vec v}{dt} \, \cdot d\vec s = m \int\limits_{AB} \, \vec v \cdot d\vec v$

Вычислим строго стоящее под знаком интеграла скалярное произведение, для чего продифференцируем по времени скалярное произведение вектора скорости самого на себя

$\frac{d}{dt}(\vec v \cdot \vec v) = \frac{d\vec v}{dt} \cdot \vec v + \vec v \cdot \frac{d\vec v}{dt} = 2 \, \vec v \cdot \frac{d\vec v}{dt} \quad (1)$

С другой стороны,

$\vec v \cdot \vec v = v^2$

Дифференцируя это равенство по времени, имеем

$\frac{d}{dt}(\vec v \cdot \vec v) = \frac{d}{dt}(v^2) = 2 \, v \, \frac{dv}{dt} \quad(2)$

Сравнивая (1) и (2) приходим к выводу, что

$\vec v \cdot d\vec v = v \, dv$

Тогда, спокойно вычисляем работу, раскрывая криволинейный интеграл через определенный, взяв в качестве пределов модуль скорости точки в начале и в конце траектории

$T = m \int\limits_{AB} \vec v \cdot d\vec v = m \int\limits_0^v v \, dv = \frac{m\,v^2}{2}$

Консервативные силы и потенциальная энергия точки

Рассмотрим действующую на точку силу, причем такую, что величина и направление этой силы зависит исключительно от положения точки в пространстве

$\vec F = \vec F(x, y, z)\quad(3)$

Пусть точка перемещается в пространстве по произвольной траектории AB. Вычислим, какую работу при этом совершит сила (3)

$A = \int\limits_{AB} \vec F \cdot d\vec s = \int\limits_{AB} \left(F_x \, dx + F_y \, dy + F_z \, dz\right)$

Так как проекции силы на оси координат зависят исключительно от этих самых координат, всегда можно найти функцию

$display$

такую, что

$F_x = \frac{\partial U}{\partial x},\quad F_y = \frac{\partial U}{\partial y},\quad F_z = \frac{\partial U}{\partial z}$

Тогда, выражение для работы преобразуется к виду

$A = \int\limits_{AB} \left(\frac{\partial U}{\partial x} \, dx + \frac{\partial U}{\partial y} \, dy + \frac{\partial U}{\partial z} \, dz\right) = \int\limits_{U_A}^{U_B} \, dU=U_B - U_A$

где $U_A,\, U_B$ — значения функции U(x, y, z) в точках A и B соответственно. Таким образом работа рассматриваемой нами силы не зависит от траектории точки, а определяется только значениями функции U в начале и в конце траектории. Такая сила называется консервативной силой, а соответствующая ей функция U(x, y, z) — силовой функцией. Очевидно, что $\vec F = \nabla\, U$ , а так же равенство нулю работы консервативной силы при движении по замкнутой траектории. Говорят так же, что функция U(x, y, z) задает в пространстве силовое поле.

Потенциальной энергией $\Pi = \Pi(x, y, z)$ точки, в пространстве с заданным силовым полем, называют работу внешних сил, приложенных к ней, которую они совершают при перемещении точки в заданное координатами (x, y, z) положение в пространстве из некоторого произвольного положения, выбранного в качестве начала отсчета уровня потенциальной энергии.

Выберем на рассмотренной ранее траектории точки произвольную точку O, лежащую между точками A и B. Положим, что в точке О потенциальная энергия равна нулю. Тогда, согласно определению

$\Pi_A = -(U_A - U_O)$

— потенциальная энергия точки в положении A, а

$\Pi_B = -(U_B - U_O)$

— потенциальная энергия точки в положении B. Учитывая всё вышесказанное снова вычислим работу потенциальных сил на перемещении из точки A в точку B

$A_{AB} = A_{AO} + A_{OB} = U_O - U_A + U_B - U_O = (U_O - U_A) - (U_O - U_B) = \Pi_A - \Pi_B$

Таким образом, работа консервативных сил равна изменению потенциальной энергии точки, взятому с обратным знаком

$A_{AB} = \Pi_A - \Pi_B = -(\Pi_B - \Pi_A) = -\Delta \Pi$

причем выбор уровня, на котором мы считаем потенциальную энергию равной нулю совершенно не влияет на результат. Отсюда можно сделать вывод, что уровень отсчета потенциальной энергии можно выбрать совершенно произвольно.

3. Понятие о вариациях обобщенных координат. Постановка вариационной задачи

Итак, рассмотрим теперь механическую систему, движущуюся под действием потенциальных сил, положение которой однозначно задается вектором обобщенных координат

$\mathbf q = \left[q_1, \, q_2, \, \dots,\, q_s \right]^T\quad(4)$

где s — число степеней свободы данной системы.

Действительный, но неизвестный пока нам, закон движения данной системы определяется зависимость обобщенных координат (4) от времени. Рассмотрим одну из обобщенных координат $inline$ , полагая аналогичные рассуждения и для всех остальных координат.

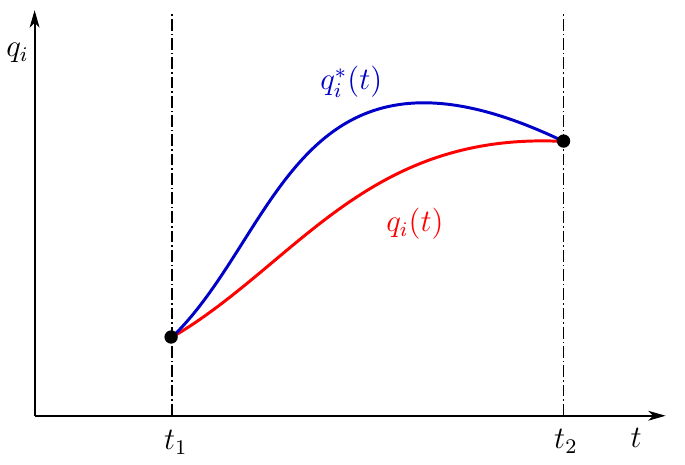
Рисунок 1. Действительное и окольное движение механической системы

На рисунке зависимость $inline$ изображена красной кривой. Выберем два произвольных фиксированных момента времени t₁ и t₂, полагая t₂ > t₁. Положение системы $\mathbf q_1 = \mathbf q(t_1)$ договоримся называть начальным положением системы, а $\mathbf q_2 = \mathbf q(t_2)$ — конечным положением системы.

Однако, я ещё раз настаиваю на том, чтобы нижеследующий текст был прочтен внимательно! Несмотря на то, что мы задаемся начальным и конечным положением системы, ни первое положение, ни второе, нам заранее неизвестны! Равно как и неизвестен закон движения системы! Эти положения рассматриваются именно как начальное и конечное положение, безотносительно конкретных значений.

Далее мы полагаем, что из начального положения в конечное система может придти разными путями, то есть зависимость $\mathbf q = \mathbf q(t)$ может быть любой кинематически возможной. Действительное движение системы будет существовать в единственном варианте (красная кривая), остальные кинематически возможные варианты будем называть окольными движениями $\mathbf q^{*} = \mathbf q^{*}(t)$ (синяя кривая на рисунке). Разность между действительным и окольным движением

$\delta q_i(t) = q^{*}_i(t) - q_i(t),\quad \forall i=\overline{1,s}\quad (5)$

будем называть изохронными вариациями обобщенных координат

В данном контексте вариации (5) следует понимать как бесконечно малые функции, выражающие отклонение окольного движения от действительного. Малая «дельта» для обозначения выбрана не случайно и подчеркивает принципиальное отличие вариации от дифференциала функции. Дифференциал — главная линейная часть приращения функции, вызванного приращением аргумента. В случае с вариацией изменение значения функции при постоянном значении аргумента вызвано изменением вида самой функции! Мы не варьируем аргумент, в роли которого выступает время, поэтому вариация называется изохронной. Мы варьируем правило по которому каждому значению времени приводится в соответствие некоторое значение обобщенных координат!

По сути, мы варьируем закон движения, по которому система из начального состояния перемещается в конечное состояние. Начальное и конечное состояние определяются действительным законом движения, но я ещё раз подчеркиваю — их конкретные значения нам не известны и могут быть любыми кинематически возможными, мы лишь полагаем, что они существуют и система гарантированно перемещается из одного положения в другое! В начальном и конечном положении системы мы не варьируем закон движения, поэтому вариации обобщенных координат в начальном и конечном положении равны нулю

$\delta q_i(t_1) = \delta q_i(t_2) = 0,\quad \forall i=\overline{1,s}\quad(6)$

Исходя из принципа наименьшего действия, действительное движение системы должно быть таким, чтобы доставлять минимум функционалу действия. Варьирование координат вызывает изменение функционала действия. Необходимым условием достижения функционалом действия экстремального значения является равенство нулю его вариации

$\delta S = \delta \int\limits_{t_1}^{t2} \, L(q_1,\dots,q_s,\,\dot q_1,\dots,\dot q_s)\,dt = 0\quad(7)$

4. Решение вариационной задачи. Уравнения Лагранжа 2-го рода

Решим поставленную нами вариационную задачу, для чего вычислим полную вариацию функционала действия и приравняем её к нулю

$\begin{align} \delta S = & \int\limits_{t_1}^{t2} \, L(q_1 + \delta q_1,\dots,q_s + \delta q_s,\,\dot q_1 + \delta\dot q_1,\dots,\dot q_s + \delta\dot q_s)\,dt - \\ &- \int\limits_{t_1}^{t2} \, L(q_1,\dots,q_s,\,\dot q_1,\dots,\dot q_s)\,dt = 0 \end{align}$

Загоним всё под один интеграл, и так как для вариаций справедливы все операции над бесконечно малыми величинами, преобразуем этот крокодил к виду

$\int\limits_{t_1}^{t_2}\left[ \sum\limits_{i=1}^s \frac{\partial L}{\partial q_i}\delta q_i + \sum\limits_{i=1}^s \frac{\partial L}{\partial \dot q_i}\delta \dot q_i \right]\,dt = 0\quad(8)$

Исходя из определения обобщенной скорости

$\delta \dot q_i = \frac{d(\delta q_i)}{dt}$

Тогда выражение (8) преобразуется к виду

$\int\limits_{t_1}^{t_2}\left[ \sum\limits_{i=1}^s \frac{\partial L}{\partial q_i}\delta q_i \, dt + \sum\limits_{i=1}^s \frac{\partial L}{\partial \dot q_i}d(\delta q_i) \right] = 0$

Второе слагаемое интегрируется по частям

$\sum\limits_{i=1}^s \frac{\partial L}{\partial \dot q_i}\delta q_i|_{t_1}^{t_2} + \int\limits_{t_1}^{t_2}\left[ \sum\limits_{i=1}^s \frac{\partial L}{\partial q_i}\delta q_i - \sum\limits_{i=1}^s \frac{d}{dt}\left(\frac{\partial L}{\partial \dot q_i}\right)\delta q_i \right]\,dt = 0\quad(10)$

Исходя из условия (7), имеем

$\sum\limits_{i=1}^s \frac{\partial L}{\partial \dot q_i}\delta q_i|_{t_1}^{t_2} = 0$

тогда, получаем уравнение

$\int\limits_{t_1}^{t_2}\left[ \sum\limits_{i=1}^s \left( \frac{\partial L}{\partial q_i} - \frac{d}{dt}\left(\frac{\partial L}{\partial \dot q_i}\right) \right) \, \delta q_i \right]\,dt = 0$

При произвольных пределах интегрирования равенство нулю определенного интеграла обеспечивается равенством нулю подынтегральной функции

$\sum\limits_{i=1}^s \left[ \frac{\partial L}{\partial q_i} - \frac{d}{dt}\left(\frac{\partial L}{\partial \dot q_i}\right) \right] \, \delta q_i = 0\quad(11)$

С учетом того, что вариации обобщенных координат независимы, (11) справедливо только в случае равенства нулю всех коэффициентов при вариациях, то есть

$\frac{\partial L}{\partial q_i} - \frac{d}{dt}\left(\frac{\partial L}{\partial \dot q_i}\right) =0, \quad \forall i = \overline{1,s}$

Никто не мешает нам умножить каждое из уравнений на (-1) и получить более привычную запись

$\frac{d}{dt}\left(\frac{\partial L}{\partial \dot q_i}\right) - \frac{\partial L}{\partial q_i} =0, \quad \forall i = \overline{1,s}\quad(12)$

Уравнения (12) и есть решение задачи. И вот на этом моменте ещё раз внимание — решение вариационной задачи по принципу наименьшего действия, это не функция, доставляющая минимум действию по Гамильтону, а система дифференциальных уравнений, решая которое таковую функцию можно найти. В данном случае это дифференциальное уравнение Лагранжа 2-го рода, записанное через функцию Лагранжа, то есть в формулировке для консервативных механических систем.

И всё, на этом принцип наименьшего действия заканчивается, а начинается теория обыкновенных дифференциальных уравнений, которая, в частности, гласит, что решением уравнения (12) является вектор-функция вида

$\mathbf q = \mathbf q(t, C_1, C_2,\dots,C_{2s})$

где C₁,...,C_2s — произвольные константы интегрирования.

Таким образом

ПНД — фундаментальный принцип, позволяющий получить уравнения движения системы, для которой определена функция Лагранжа

Точка! В задачах аналитической механики вышеперечисленные выкладки больше не нужно проделывать, достаточно использовать их результат (12). Функция, удовлетворяющая уравнению (12) есть закон движения системы, удовлетворяющей ПНД.

5. Задача с шариком и стенкой

Теперь вернемся к той задаче, с которой всё началось — об одномерном движении шарика около абсолютно упругой стенки. Разумеется, для данной задачи можно получить дифференциальные уравнения движения. Так как это дифференциальные уравнения движения, то любое, я подчеркиваю это, любое их решение доставляет минимум функционалу действия, а значит ПНД выполняется! Общее решение уравнений движения шарика можно изобразить в виде так называемого фазового портрета рассматриваемой механической системы. Вот этот фазовый портрет

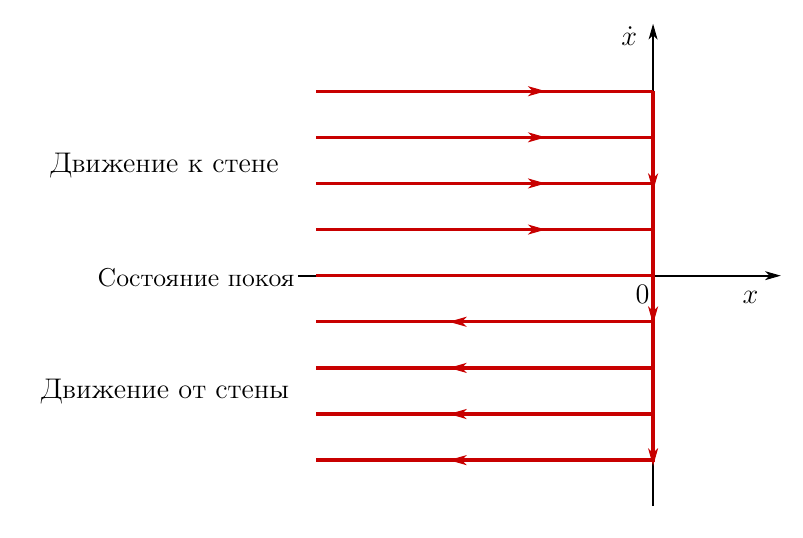
Рисунок 2. Фазовый портрет системы в задаче с шариком

По горизонтальной оси откладывается координата шарика, по вертикальной — проекция скорости на ось x. Может это покажется странным, но данный чертеж отражает все возможные фазовые траектории движения шарика, при любых начальных, или если вам так хочется, краевых условиях. На самом деле параллельных прямых на графике бесконечно много, на чертеже показаны некоторые из них и направление движения по фазовой траектории.

Это — общее решение уравнения движения шарика. Каждая из этих фазовых траекторий доставляет минимум функционалу действия, что непосредственно следует из выкладок, проделанных выше.

Что делает автор задачи? Он говорит: вот шарик покоится, и за промежуток времени от t_A до t_B действие равно нулю. Если шарик толкнуть к стенке, то за тот же промежуток времени действие будет больше, так как у шарика отличная от нуля и неизменная кинетическая энергия. Но почему шарик движется к стенке, ведь в покое действие будет меньше? Значит ПНД испытвает проблемы и не работает! Но мы обязательно решим это в следующей статье.

То что говорит автор — бред. Почему? Да потому, что он сравнивает действия на различных ветвях одной и той же действительной фазовой траектории! Между тем, при применении ПНД, сравнивается действие на действительной траектории и на множестве окольных траекторий. То есть происходит сравнение действия на реальной траектории с действием на тех траекториях, которых нет в природе, и никогда не будет!

Не понятно? Объясню ещё более доходчиво. Рассмотрим состояние покоя. Оно описывается ветвью фазового портрета, совпадающего с осью абсцисс. Координата не меняется с течением времени. Это действительное движение. А какое же движение будет окольным. Любое другое кинематически возможное. Например малые колебания шарика около рассматриваемого нами положения покоя. Задача допускает колебания шарика вдоль оси х? Допускает, значит такое движение кинематически возможно и может рассматриваться как одно их окольных

Почему же шарик таки покоится? Да потому, что действие в состоянии покоя, вычисленное на фиксированном промежутке времени от t_A до t_B, будет меньше действия, при малых колебаниях на том же промежутке времени. Значит колебаниям и любому другому «шевелению» шарика природа предпочитает покой. В полном соответствии с ПНД.

Допустим мы толкнули шарик в сторону стенки. Пусть мы толкнули его как хочет автор, со скоростью, подобранной из краевых условий, так чтобы в момент времени t_B шарик оказался в том же положении, откуда стартовал. Шарик, с постоянной скоростью долетит до стенки, упруго отскочит и вернется в начальное положение в момент времени t_B, опять таки с постоянной скоростью. Ок, это действительное движение. Какое движение будет одним из окольных? Например, если шарик будет двигаться к стенке и от стенки со скоростью, меняющейся со временем. Такое движение возможно кинематически? Возможно. Почему же модуль скорости шарика не меняется? Да потому, что действие на такой фазовой траектории будет иметь минимальное значение, в сравнении с любом другим вариантом, где скорость зависит от времени.

Вот и всё. Ничего такого волшебного тут не происходит. ПНД работает безо всяких проблем.

Выводы и пожелания

ПНД — фундаментальный закон природы. Из него, в частности, вытекают законы механики, например дифференциальные уравнения движения (12). ПНД говорит нам о том, что природа устроена так, что уравнение движения консервативной механической системы выглядит именно как выражение (12) и никак иначе. Большего от него и не требуется.

Не нужно придумывать проблем там где их нет.

Теги:

Хабы:

Принцип наименьшего действия в аналитической механике

Предыстория

Не все так просто

1. Определение действия по Гамильтону. Принцип наименьшего действия

2. Границы применимости принципа наименьшего действия. Некоторые определения для самых маленьких

3. Понятие о вариациях обобщенных координат. Постановка вариационной задачи

4. Решение вариационной задачи. Уравнения Лагранжа 2-го рода

5. Задача с шариком и стенкой

Выводы и пожелания

Публикации

Истории

Ближайшие события