Ни для кого не секрет, что одна из любимых забав для разработчика программного обеспечения – прохождение собеседований с работодателями. Все мы занимаемся этим время от времени и совершенно по разным причинам. Причем самая очевидная из них – поиск работы – думаю, не самая распространенная. Посещение интервью – это неплохой способ держать себя в форме, повторять забытые основы и узнавать что-то новое. А в случае успеха, еще и повышать уверенность в своих силах. Нам становится скучно, мы выставляем себе статус «открыт для предложений» в какой-нибудь «деловой» социальной сети вроде «LinkedIn» – и армия менеджеров человеческих ресурсов уже атакует наши ящики для входящих сообщений.

В процессе, пока весь этот бедлам творится, мы сталкиваемся со множеством вопросов, которые, как говорят по ту сторону подразумеваемо-обвалившегося занавеса, «ring a bell», а их подробности скрылись за туманом войны. Вспоминаются они чаще всего лишь на зачетах по алгоритмам и структурам данных (лично у меня таких вовсе не было) и собственно собеседованиях.
Один из самых распространенных вопросов на собеседовании на должность программиста любой специализации – это списки. Например, односвязные списки. И связанные с ними базовые алгоритмы. Например, разворот. И обычно это происходит как-то так: «Хорошо, а как бы вы развернули односвязный список?» Главное – застать этим вопросом соискателя врасплох.
Собственно, это все и привело меня к мысли написать этот небольшой обзор для постоянного напоминания и назидания. Итак, шутки в сторону, behold!
Связный список – это одна из базовых структур данных. Каждый элемент (или узел) ее состоит из, собственно, хранимых данных и ссылок на соседние элементы. Односвязный список хранит ссылку только на следующий элемент в структуре, а двусвязный – на следующий и предыдущий. Такая организация данных позволяет им располагаться в любой области памяти (в отличие от, например, массива, все элементы которого должны располагаться в памяти один за другим).
Про списки можно много чего еще сказать, конечно: они могут быть кольцевыми (т.е. последний элемент хранит ссылку на первый) или нет (т.е. ссылка у последнего элемента отсутствует). Списки могут быть типизированными, т.е. содержать данные одного типа, или нет. И прочее, и прочее.
Лучше попробуем написать немного кода. Например, как-нибудь так можно представить узел списка:
«Generic»–тип, который в поле
Сам список исчерпывающе идентифицируется своим первым узлом:
Первый узел объявлен опциональным, потому что список вполне может быть и пустым.
По идее, конечно, в классе надо реализовать все необходимые методы – вставка, удаление, доступ к узлам и пр., но мы этим займемся как-нибудь в другой раз. Заодно проверим, будет ли использование
Пора заняться делом, ради которого мы сегодня здесь собрались! А наиболее эффективно им заняться можно двумя способами. Первый – это простой цикл, от первого до последнего узла.
Цикл работает с тремя переменными, которым перед началом присваивается значение предыдущего, текущего и следующего узла. (В этот момент значение предыдущего узла, естественно, пустое.) Цикл начинается с проверки того, что следующий узел – не пустой, и, если это так, выполняется тело цикла. В цикле не происходит никакой магии: у текущего узла полю, ссылающемуся на следующий элемент, присваивается ссылка на предыдущий (на первой итерации значение ссылки, соответственно, обнуляется, что соответствует положению дел в последнем узле). Ну и дальше переменным соответствующим предыдущему, текущему и следующему узлу присваиваются новые значения. После выхода из цикла текущему (т.е. вообще последнему итерируемому) узлу присваивается новое значение ссылки на следующий узел, т.к. выход из цикла происходит как раз в момент, когда последний узел в списке становится текущим.
На словах, конечно, все это звучит странно и непонятно, поэтому лучше посмотрим код:
Для проверки воспользуемся списком узлов, полезная нагрузка которых представляют собой простые целочисленные идентификаторы. Создадим список из десяти элементов:
Вроде все хорошо, но мы с вами люди, а не компьютеры, и нам хорошо бы получить визуальное доказательство корректности созданного списка и описанного выше алгоритма. Пожалуй, простого вывода на печать будет достаточно. Чтобы вывод сделать читаемым, добавим реализации протокола
…И соответствующему списку, чтобы вывести все узлы по порядку:
Строковое представление наших типов будет содержать адрес в памяти и целочисленный идентификатор. С помощью них организуем вывод на печать сгенерированного списка из десяти узлов:
Развернем этот список и выведем его на печать снова:
Можно заметить, что адреса в памяти списка и узлов не изменились, а узлы списка напечатались в обратном порядке. Ссылки на следующий элемент узла теперь указывают на предыдущий (т.е., например, следующий элемент узла «5» теперь не «6», а «4»). И это означает, что у нас получилось!
Второй известный способ сделать такой же разворот основан на рекурсии. Для его реализации объявим функцию, которая принимает первый узел списка, а возвращает уже «новый» первый узел (который до этого был последним).
Параметр и возвращаемое значение – опциональные, потому что внутри этой функции она вызывается снова и снова на каждом следующем узле, пока тот не будет пустым (т.е. пока не достигнут конец списка). Соответственно, в теле функции необходимо проверить не пуст ли узел, на котором вызвана функция и имеется ли у этого узла следующий. Если нет, то функция возвращает то же, что было передано в аргумент.
Вообще-то я честно попытался описать полный алгоритм словами, но в итоге стер почти все, потому что результат было бы невозможно понять. Рисовать блок-схемы и формально описывать шаги алгоритма – также в данном случае, думаю, смысла не имеет, потому что нам с вами будет удобней просто прочитать и попробовать осмыслить код на «Swift»:
Сам алгоритм «обернут» методом типа собственно списка, для удобства вызова.
Выглядит покороче, но, на мой взгляд, сложнее для понимания.
Вызовем этот метод на результате предыдущего разворота и выведем на печать новый результат:
Из вывода видно, что все адреса в памяти снова не изменились, а узлы теперь следуют в первоначальном порядке (т.е. «развернулись» еще раз). А это означает, что мы снова справились!
Если взглянуть на методы разворота внимательно (или провести эксперимент с подсчетом вызовов), можно заметить, что цикл в первом случае и внутренний (рекурсивный) вызов метода во втором случае происходят на один раз меньше, чем количество узлов в списке (в нашем случае, девять раз). Также можно обратить внимание на то, что происходит вокруг цикла в первом случае – та же череда присваиваний – и на первый, не рекурсивный, вызов метода во втором случае. Получается, что в обоих случаях «круг» повторяется ровно десять раз для списка из десяти узлов. Таким образом, мы имеем линейную сложность для обоих алгоритмов – O(n).
Вообще говоря, два описанных алгоритма считаются наиболее эффективными для решения данной задачи. Что касается вычислительной сложности, то возможность придумать алгоритм с более низким ее значением, не представляется возможным: так или иначе необходимо «посетить» каждый узел для присваивания нового значения для хранимой внутри ссылки.
Еще одна характеристика, которую стоит упомянуть – это «сложность по выделяемой памяти». Оба предложенных алгоритма создают фиксированное число новых переменных (три в первом случае и одна – во втором). Это означает, что объем выделяемой памяти не зависит от количественной характеристики входных данных и описывается константной функцией – O(1).
Но, на самом деле, во втором случае это не так. Опасность рекурсии в том, что для каждого рекурсивного вызова на стеке выделяется дополнительная память. В нашем случае глубина рекурсии соответствует количеству входных данных.
И наконец, я решил поэкспериментировать еще немного: простым и примитивным способом замерил абсолютное время выполнения двух методов для разного количества входных данных. Вот так:
И вот что у меня получилось (это «сырые» данные из «Playground»):
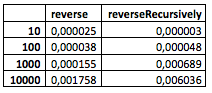
(Бóльшие значения мой компьютер, к сожалению, уже не осилил.)
Что можно увидеть из таблицы? Пока ничего особенного. Хотя уже заметно, что рекурсивный метод ведет себя чуть хуже при относительно малом количестве узлов, но где-то между 100 и 1000 начинает показывать себя лучше.
Также я попробовал тот же простой тест внутри полноценного «Xcode»-проекта. Результаты получились такие:
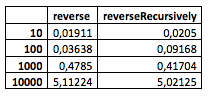
Во-первых, стоит упомянуть, что результаты получены после активации режима «агрессивной» оптимизации, направленной на скорость исполнения (
Я постарался осветить довольно классическую тему с точки зрения своего любимого на данный момент языка программирования и, надеюсь, вам было любопытно следить за прогрессом также, как и мне самому. А еще я очень рад, если вам удалось узнать и что-нибудь новое – тогда я точно не зря потратил время на эту статью (вместо того, чтобы сидеть и смотреть сериалы).
Если у кого-то есть желание отслеживать мою общественную активность, вот ссылка на мой «Twitter», где первым делом появляются ссылки на мои новые посты и еще немного, сверх того.

В процессе, пока весь этот бедлам творится, мы сталкиваемся со множеством вопросов, которые, как говорят по ту сторону подразумеваемо-обвалившегося занавеса, «ring a bell», а их подробности скрылись за туманом войны. Вспоминаются они чаще всего лишь на зачетах по алгоритмам и структурам данных (лично у меня таких вовсе не было) и собственно собеседованиях.
Один из самых распространенных вопросов на собеседовании на должность программиста любой специализации – это списки. Например, односвязные списки. И связанные с ними базовые алгоритмы. Например, разворот. И обычно это происходит как-то так: «Хорошо, а как бы вы развернули односвязный список?» Главное – застать этим вопросом соискателя врасплох.
Собственно, это все и привело меня к мысли написать этот небольшой обзор для постоянного напоминания и назидания. Итак, шутки в сторону, behold!
Односвязный список
Связный список – это одна из базовых структур данных. Каждый элемент (или узел) ее состоит из, собственно, хранимых данных и ссылок на соседние элементы. Односвязный список хранит ссылку только на следующий элемент в структуре, а двусвязный – на следующий и предыдущий. Такая организация данных позволяет им располагаться в любой области памяти (в отличие от, например, массива, все элементы которого должны располагаться в памяти один за другим).
Про списки можно много чего еще сказать, конечно: они могут быть кольцевыми (т.е. последний элемент хранит ссылку на первый) или нет (т.е. ссылка у последнего элемента отсутствует). Списки могут быть типизированными, т.е. содержать данные одного типа, или нет. И прочее, и прочее.
Лучше попробуем написать немного кода. Например, как-нибудь так можно представить узел списка:
final class Node<T> { let payload: T var nextNode: Node? init(payload: T, nextNode: Node? = nil) { self.payload = payload self.nextNode = nextNode } }
«Generic»–тип, который в поле
payload способен хранить полезную нагрузку любого типа.Сам список исчерпывающе идентифицируется своим первым узлом:
final class SinglyLinkedList<T> { var firstNode: Node<T>? init(firstNode: Node<T>? = nil) { self.firstNode = firstNode } }
Первый узел объявлен опциональным, потому что список вполне может быть и пустым.
По идее, конечно, в классе надо реализовать все необходимые методы – вставка, удаление, доступ к узлам и пр., но мы этим займемся как-нибудь в другой раз. Заодно проверим, будет ли использование
struct (на что нас активно поощряют «Apple» своим примером) более выгодным выбором, и, возможно, вспомним о «Copy-on-write»-подходе.Разворот односвязного списка
Первый способ. Цикл
Пора заняться делом, ради которого мы сегодня здесь собрались! А наиболее эффективно им заняться можно двумя способами. Первый – это простой цикл, от первого до последнего узла.
Цикл работает с тремя переменными, которым перед началом присваивается значение предыдущего, текущего и следующего узла. (В этот момент значение предыдущего узла, естественно, пустое.) Цикл начинается с проверки того, что следующий узел – не пустой, и, если это так, выполняется тело цикла. В цикле не происходит никакой магии: у текущего узла полю, ссылающемуся на следующий элемент, присваивается ссылка на предыдущий (на первой итерации значение ссылки, соответственно, обнуляется, что соответствует положению дел в последнем узле). Ну и дальше переменным соответствующим предыдущему, текущему и следующему узлу присваиваются новые значения. После выхода из цикла текущему (т.е. вообще последнему итерируемому) узлу присваивается новое значение ссылки на следующий узел, т.к. выход из цикла происходит как раз в момент, когда последний узел в списке становится текущим.
На словах, конечно, все это звучит странно и непонятно, поэтому лучше посмотрим код:
extension SinglyLinkedList { func reverse() { var previousNode: Node<T>? = nil var currentNode = firstNode var nextNode = firstNode?.nextNode while nextNode != nil { currentNode?.nextNode = previousNode previousNode = currentNode currentNode = nextNode nextNode = currentNode?.nextNode } currentNode?.nextNode = previousNode firstNode = currentNode } }
Для проверки воспользуемся списком узлов, полезная нагрузка которых представляют собой простые целочисленные идентификаторы. Создадим список из десяти элементов:
let node = Node(payload: 0) // T == Int let list = SinglyLinkedList(firstNode: node) var currentNode = node var nextNode: Node<Int> for id in 1..<10 { nextNode = Node(payload: id) currentNode.nextNode = nextNode currentNode = nextNode }
Вроде все хорошо, но мы с вами люди, а не компьютеры, и нам хорошо бы получить визуальное доказательство корректности созданного списка и описанного выше алгоритма. Пожалуй, простого вывода на печать будет достаточно. Чтобы вывод сделать читаемым, добавим реализации протокола
CustomStringConvertible узлу с целочисленным идентификатором:extension Node: CustomStringConvertible where T == Int { var description: String { let firstPart = """ Node \(Unmanaged.passUnretained(self).toOpaque()) has id \(payload) and """ if let nextNode = nextNode { return firstPart + " next node \(nextNode.payload)." } else { return firstPart + " no next node." } } }
…И соответствующему списку, чтобы вывести все узлы по порядку:
extension SinglyLinkedList: CustomStringConvertible where T == Int { var description: String { var description = """ List \(Unmanaged.passUnretained(self).toOpaque()) """ if firstNode != nil { description += " has nodes:\n" var node = firstNode while node != nil { description += (node!.description + "\n") node = node!.nextNode } return description } else { return description + " has no nodes." } } }
Строковое представление наших типов будет содержать адрес в памяти и целочисленный идентификатор. С помощью них организуем вывод на печать сгенерированного списка из десяти узлов:
print(String(describing: list)) /* List 0x00006000012e1a60 has nodes: Node 0x00006000012e2380 has id 0 and next node 1. Node 0x00006000012e8d40 has id 1 and next node 2. Node 0x00006000012e8d20 has id 2 and next node 3. Node 0x00006000012e8ce0 has id 3 and next node 4. Node 0x00006000012e8ae0 has id 4 and next node 5. Node 0x00006000012e89a0 has id 5 and next node 6. Node 0x00006000012e8900 has id 6 and next node 7. Node 0x00006000012e8a40 has id 7 and next node 8. Node 0x00006000012e8a60 has id 8 and next node 9. Node 0x00006000012e8820 has id 9 and no next node. */
Развернем этот список и выведем его на печать снова:
list.reverse() print(String(describing: list)) /* List 0x00006000012e1a60 has nodes: Node 0x00006000012e8820 has id 9 and next node 8. Node 0x00006000012e8a60 has id 8 and next node 7. Node 0x00006000012e8a40 has id 7 and next node 6. Node 0x00006000012e8900 has id 6 and next node 5. Node 0x00006000012e89a0 has id 5 and next node 4. Node 0x00006000012e8ae0 has id 4 and next node 3. Node 0x00006000012e8ce0 has id 3 and next node 2. Node 0x00006000012e8d20 has id 2 and next node 1. Node 0x00006000012e8d40 has id 1 and next node 0. Node 0x00006000012e2380 has id 0 and no next node. */
Можно заметить, что адреса в памяти списка и узлов не изменились, а узлы списка напечатались в обратном порядке. Ссылки на следующий элемент узла теперь указывают на предыдущий (т.е., например, следующий элемент узла «5» теперь не «6», а «4»). И это означает, что у нас получилось!
Второй способ. Рекурсия
Второй известный способ сделать такой же разворот основан на рекурсии. Для его реализации объявим функцию, которая принимает первый узел списка, а возвращает уже «новый» первый узел (который до этого был последним).
Параметр и возвращаемое значение – опциональные, потому что внутри этой функции она вызывается снова и снова на каждом следующем узле, пока тот не будет пустым (т.е. пока не достигнут конец списка). Соответственно, в теле функции необходимо проверить не пуст ли узел, на котором вызвана функция и имеется ли у этого узла следующий. Если нет, то функция возвращает то же, что было передано в аргумент.
Вообще-то я честно попытался описать полный алгоритм словами, но в итоге стер почти все, потому что результат было бы невозможно понять. Рисовать блок-схемы и формально описывать шаги алгоритма – также в данном случае, думаю, смысла не имеет, потому что нам с вами будет удобней просто прочитать и попробовать осмыслить код на «Swift»:
extension SinglyLinkedList { func reverseRecursively() { func reverse(_ node: Node<T>?) -> Node<T>? { guard let head = node else { return node } if head.nextNode == nil { return head } let reversedHead = reverse(head.nextNode) head.nextNode?.nextNode = head head.nextNode = nil return reversedHead } firstNode = reverse(firstNode) } }
Сам алгоритм «обернут» методом типа собственно списка, для удобства вызова.
Выглядит покороче, но, на мой взгляд, сложнее для понимания.
Вызовем этот метод на результате предыдущего разворота и выведем на печать новый результат:
list.reverseRecursively() print(String(describing: list)) /* List 0x00006000012e1a60 has nodes: Node 0x00006000012e2380 has id 0 and next node 1. Node 0x00006000012e8d40 has id 1 and next node 2. Node 0x00006000012e8d20 has id 2 and next node 3. Node 0x00006000012e8ce0 has id 3 and next node 4. Node 0x00006000012e8ae0 has id 4 and next node 5. Node 0x00006000012e89a0 has id 5 and next node 6. Node 0x00006000012e8900 has id 6 and next node 7. Node 0x00006000012e8a40 has id 7 and next node 8. Node 0x00006000012e8a60 has id 8 and next node 9. Node 0x00006000012e8820 has id 9 and no next node. */
Из вывода видно, что все адреса в памяти снова не изменились, а узлы теперь следуют в первоначальном порядке (т.е. «развернулись» еще раз). А это означает, что мы снова справились!
Выводы
Если взглянуть на методы разворота внимательно (или провести эксперимент с подсчетом вызовов), можно заметить, что цикл в первом случае и внутренний (рекурсивный) вызов метода во втором случае происходят на один раз меньше, чем количество узлов в списке (в нашем случае, девять раз). Также можно обратить внимание на то, что происходит вокруг цикла в первом случае – та же череда присваиваний – и на первый, не рекурсивный, вызов метода во втором случае. Получается, что в обоих случаях «круг» повторяется ровно десять раз для списка из десяти узлов. Таким образом, мы имеем линейную сложность для обоих алгоритмов – O(n).
Вообще говоря, два описанных алгоритма считаются наиболее эффективными для решения данной задачи. Что касается вычислительной сложности, то возможность придумать алгоритм с более низким ее значением, не представляется возможным: так или иначе необходимо «посетить» каждый узел для присваивания нового значения для хранимой внутри ссылки.
Еще одна характеристика, которую стоит упомянуть – это «сложность по выделяемой памяти». Оба предложенных алгоритма создают фиксированное число новых переменных (три в первом случае и одна – во втором). Это означает, что объем выделяемой памяти не зависит от количественной характеристики входных данных и описывается константной функцией – O(1).
Но, на самом деле, во втором случае это не так. Опасность рекурсии в том, что для каждого рекурсивного вызова на стеке выделяется дополнительная память. В нашем случае глубина рекурсии соответствует количеству входных данных.
И наконец, я решил поэкспериментировать еще немного: простым и примитивным способом замерил абсолютное время выполнения двух методов для разного количества входных данных. Вот так:
let startDate = Date().timeIntervalSince1970 // list.reverse() / list.reverseRecursively() let finishDate = Date().timeIntervalSince1970 let runningTime = finishDate – startDate // Seconds
И вот что у меня получилось (это «сырые» данные из «Playground»):

(Бóльшие значения мой компьютер, к сожалению, уже не осилил.)
Что можно увидеть из таблицы? Пока ничего особенного. Хотя уже заметно, что рекурсивный метод ведет себя чуть хуже при относительно малом количестве узлов, но где-то между 100 и 1000 начинает показывать себя лучше.
Также я попробовал тот же простой тест внутри полноценного «Xcode»-проекта. Результаты получились такие:

Во-первых, стоит упомянуть, что результаты получены после активации режима «агрессивной» оптимизации, направленной на скорость исполнения (
-Ofast), отчасти поэтому числа столь малы. Также интересно то, что в этом случае рекурсивный метод показал себя чуть лучше, наоборот, лишь на очень малых размерах входных данных, а уже на списке из 100 узлов, метод проигрывает. Из 100000 – он и вовсе заставил программу завершиться аварийно.Заключение
Я постарался осветить довольно классическую тему с точки зрения своего любимого на данный момент языка программирования и, надеюсь, вам было любопытно следить за прогрессом также, как и мне самому. А еще я очень рад, если вам удалось узнать и что-нибудь новое – тогда я точно не зря потратил время на эту статью (вместо того, чтобы сидеть и смотреть сериалы).
Если у кого-то есть желание отслеживать мою общественную активность, вот ссылка на мой «Twitter», где первым делом появляются ссылки на мои новые посты и еще немного, сверх того.
