 Эта статья получилась из вопроса, который я сам себе задал вчера.
Эта статья получилась из вопроса, который я сам себе задал вчера. «Существует ли год, в котором ни один месяц не начинается в понедельник?»На первый взгляд — да. Год может начинаться с любого дня недели, месяцы тоже каждый раз начинаются в разные дни недели. Вариантов множество, скорее всего, найдётся и не один такой год.
Так я подумал в первую минуту после того, как задался вопросом. Это следовало бы доказать. Перебрать все года, например. Простой и быстрый способ, но не интересный. Доказать математически было намного более заманчивой идеей, но как к этому подступиться я совершенно не понимал. Поэтому просто начал выписывать продолжительность каждого месяца на бумагу.
Тут стоит оговорить, что речь дальше пойдёт про григорианский календарь, по которому мы живём с 1918 года. Однако часть рассуждений будет верна и для юлианского.
На самом деле такого года не существует. Давайте разбираться почему.
Часть 1. Месяцы
Сначала вспомним, сколько дней в каждом месяце:
| Янв | Фев | Март | Апр | Май | Июнь | Июль | Авг | Сен | Окт | Нояб | Дек |
| 31 | 28 / 29 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 31 |
| Янв | Фев | Март | Апр | Май | Июнь | Июль | Авг | Сен | Окт | Нояб | Дек |
| 3 | 0 / 1 | 3 | 2 | 3 | 2 | 3 | 3 | 2 | 3 | 2 | 3 |
если в месяце (28 + N) дней, то первое число следующего месяца сдвинется на N дней относительно дня недели первого числа текущего месяца.Например, в этом году январь начался во вторник, поэтому февраль начался в пятницу. Вт + 3 = Пт.
Насколько же сдвинут день недели первого числа некоторого месяца? Чтобы найти это, надо просуммировать «излишки» дней над четырьмя неделями во всех предыдущих месяцах. В таблице представлены сдвиги относительно дня недели на первое января. Первая строка для невисокосного года, вторая для високосного.
| Янв | Фев | Март | Апр | Май | Июнь | Июль | Авг | Сен | Окт | Нояб | Дек |
| 0 | 3 | 3 | 6 | 8 | 11 | 13 | 16 | 19 | 21 | 24 | 26 |
| 0 | 3 | 4 | 7 | 9 | 12 | 14 | 17 | 20 | 22 | 25 | 27 |
| Янв | Фев | Март | Апр | Май | Июнь | Июль | Авг | Сен | Окт | Нояб | Дек |
| 0 | 3 | 3 | 6 | 1 | 4 | 6 | 2 | 5 | 0 | 3 | 5 |
| 0 | 3 | 4 | 0 | 2 | 5 | 0 | 3 | 6 | 1 | 4 | 6 |
Мы получили ответ на вопрос в начале статьи.
Так как для обоих вариантов года в таблице присутствуют все сдвиги от 0 до 6, то в любом году есть месяц, который начинается в какой-то определённый день недели.Но теперь можно задавать другие воп��осы. Например, «в каких годах такой месяц только один?» или «в какие года таких месяцев максимально много?». Для этого надо уметь определять день недели на первое января любого года.
Часть 2. Годы
Когда я учился программировать, а это было в 10 классе школы на PascalABC, одним из первых серьёзных заданий было реализовать процедуру, распечатывающую календарь на год, который передавался как аргумент. У нас были подсказки, какие функции для этого надо реализовать. В целом всё сводилось к подсчёту дней между двумя датами: эталонной и текущей, чтобы определить день недели на первое января нужного года.
Такой подход работал, но скорость зависела от того, насколько близко необходимый год к эталонному. Меня это расстраивало, но придумать что-то лучше я тогда не смог. Теперь же настал идеальный момент, чтобы до конца разобраться в этом.
Високосные года в григорианском календаре назначаются следующим образом:
Из этого описания видно, что цикл високосности имеет период в 400 лет. Но не ясно, будут ли такие четырёхсотлетние циклы начинаться в один и тот же день недели.
- год, номер которого кратен 400, — високосный
- остальные года, номер которых кратен 100, — невисокосные
- остальные года, номер которых кратен 4, — високосные
- остальные года — невисокосные
Заметим, что первое января от года к году смещается на один или два дня недели, и напишем
немного кода.
bool is_leap_year(int year) { if ((year % 400) == 0) return true; if ((year % 100) == 0) return false; if ((year % 4) == 0) return true; return false; } void first_weekdays_table() { ofstream file("weekdays.txt", ios_base::out); int weekday = 3; for (int i = 1801; i <= 3000; ++i) { file << weekday; if ((i % 100) != 0) { file << " "; } else { file << endl; } weekday += is_leap_year(i) ? 2 : 1; weekday %= 7; } file.close(); }
Выводятся дни недели на первое января каждого года, с 1801 до 3000. Понедельник обозначается как «0», вторник как «1», и т. д. Представим всё в виде таблицы из двух полных четырёхсотлетних циклов и двух половинок. По горизонтали идут столетия, по вертикали года в этих столетиях. В ячейки на пересечении столетия и года написан день недели, в который этот год начался. Например, день недели, в который начался 1997 год, стоит на пересечении столбца «1900» и строки «97». Это среда. Полная версия таблицы: часть 1, часть 2.
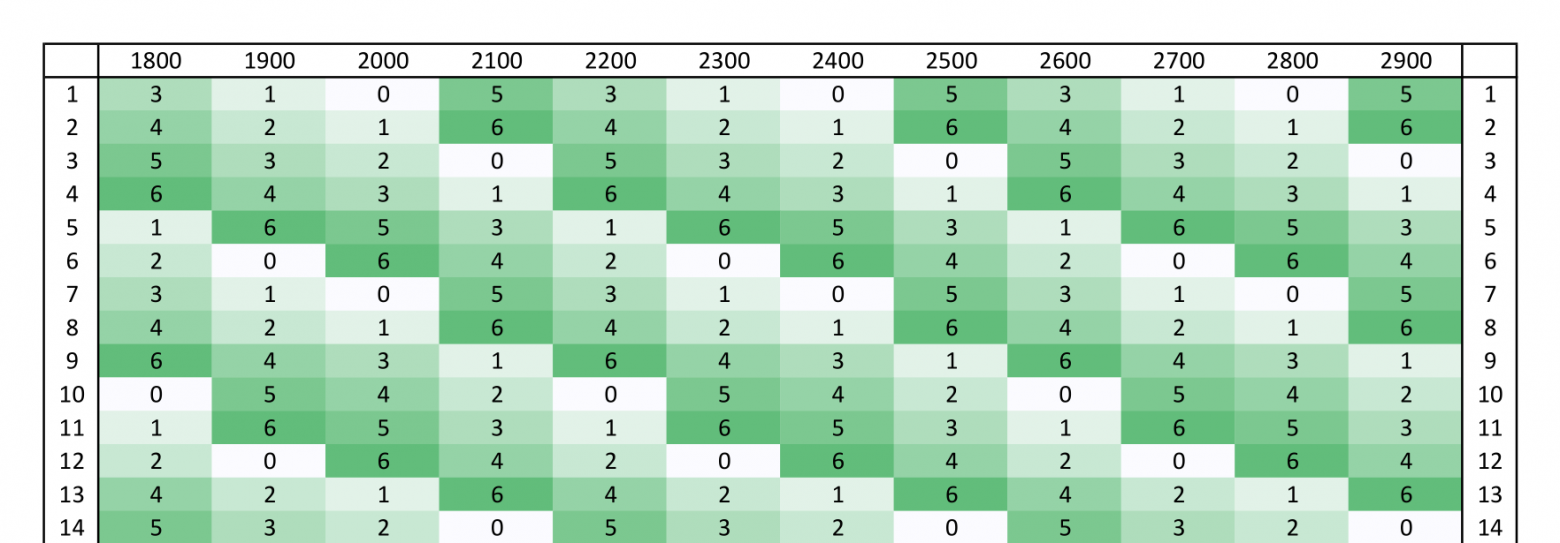
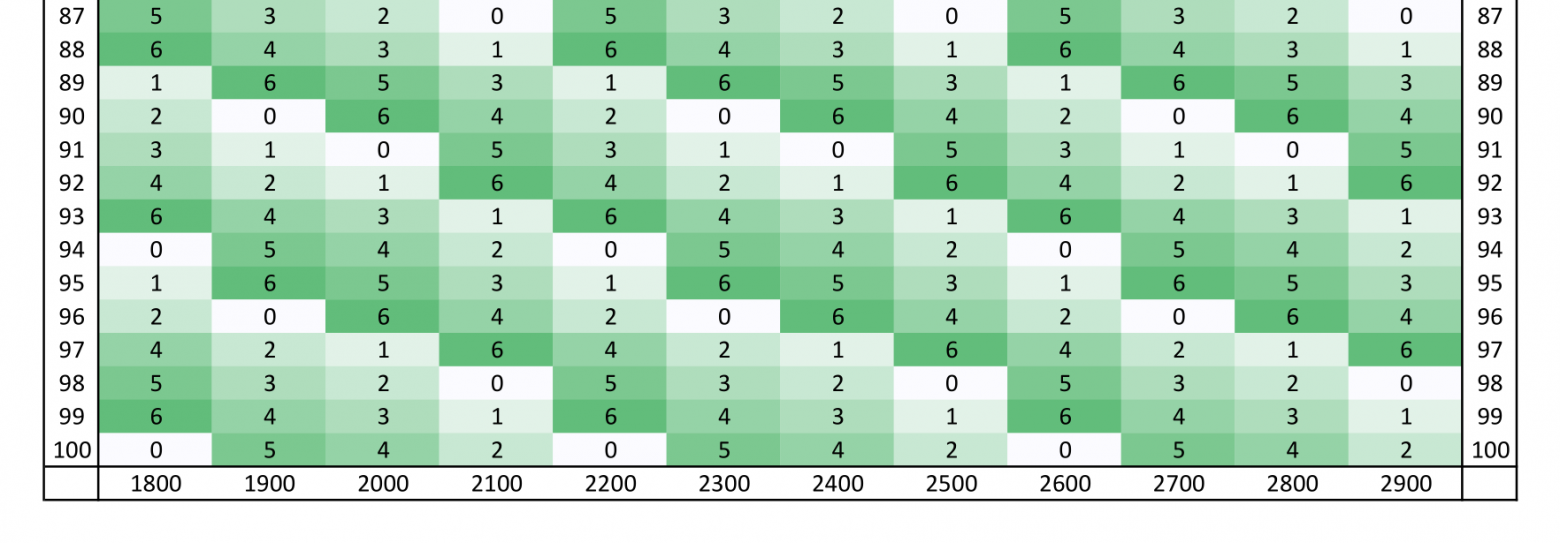
В таблице сразу можно заметить две вещи: четырёхсотлетние циклы действительно начинаются в один день недели (2001, 2401 и 2801 года; понедельник), а вместо 2000 года есть «тысяча девятьсот сотый». Последнее сделано нарочно, для дальнейшего удобства. Первый же факт позволяет нам без препятствий двигаться дальше.
В григорианском календаре все четырёхсотлетние циклы начинаются в понедельник.Но самое интересное кроется в полной версии таблицы. Можно обнаружить, что каждое столетие внутри четырёхсотлетнего цикла состоит из повторяющегося двадцативосьмилетнего цикла:
| 0 | 1 | 2 | 3 | 5 | 6 | 0 | 1 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 | 6 | 0 | 1 | 2 | 4 | 5 | 6 | 0 | 2 | 3 | 4 | 5 |
Первое столетие начинается со смещением по циклу, равным 0, второе со смещением 4, третье со смещением 8 и четвёртое со смещением 12. Именно для этого таблица представлена в виде, где в столетии есть «сотые» года и нет нулевых. Стоит сказать, что всего существует 14 различных вариантов года. В двадцативосьмилетнем цикле по одному разу на каждый день недели приходится начало високосного года и по три раза начало не високосного.
Теперь мы можем определить день недели для любой даты, не используя опорных дат. Для этого нам надо понять, в каком столетии внутри четырёхсотлетнего цикла находится год и какой он по счёту в этом столетии. По таблице определим день недели на первое января года, а с помощью первой части статьи — день недели в конкретное число нужного месяца. Вместо тысячи слов
напишем ещё немного кода.
int get_weekday(int year, int month, int day) { int weekdays[] = {0, 1, 2, 3, 5, 6, 0, 1, 3, 4, 5, 6, 1, 2, 3, 4, 6, 0, 1, 2, 4, 5, 6, 0, 2, 3, 4, 5}; int shift_not_leap[] = {0, 3, 3, 6, 1, 4, 6, 2, 5, 0, 3, 5}; int shift_leap[] = {0, 3, 4, 0, 2, 5, 0, 3, 6, 1, 4, 6}; bool is_leap = is_leap_year(year); year -= 1; year %= 400; int century = year / 100; year %= 100; int index = (year + (4 * century)) % 28; int weekday = weekdays[index]; weekday += is_leap ? shift_leap[month - 1] : shift_not_leap[month - 1]; weekday += (day - 1); weekday %= 7; return weekday; }
Часть 3. Итоги
С помощью всего двух таблиц можно определить день недели для любой даты, не используя при этом опорных дат.
Последовательность дней недели на первое января в двадцативосьмилетнем цикле:
| 0 | 1 | 2 | 3 | 5 | 6 | 0 | 1 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 | 6 | 0 | 1 | 2 | 4 | 5 | 6 | 0 | 2 | 3 | 4 | 5 |
И таблица смещений дней недели на первое число каждого месяца для невисокосного и високосного годов:
| Янв | Фев | Март | Апр | Май | Июнь | Июль | Авг | Сен | Окт | Нояб | Дек |
| 0 | 3 | 3 | 6 | 1 | 4 | 6 | 2 | 5 | 0 | 3 | 5 |
| 0 | 3 | 4 | 0 | 2 | 5 | 0 | 3 | 6 | 1 | 4 | 6 |
Интересный факт: с 1 по 13 февраля 1918 года в Советской России не родился ни один человек.
Задавайте себе вопросы с утра по воскресеньям =)
Обновление от 03.07.2019 (среда)
Если представить двадцативосьмилетний цикл в виде таблицы,
0, 1, 2, 3, 5, 6, 0, 1, 3, 4, 5, 6, 1, 2, 3, 4, 6, 0, 1, 2, 4, 5, 6, 0, 2, 3, 4, 5
то становится понятно, как можно вычислить смещение дня недели на первое января:
weekday = (index + (index / 4)) % 7;
С учётом этого, а также того, что смещения для месяцев в високосном году можно вычислить через смещения в невисокосном, напишем
следующую функцию
int get_weekday_c(int year, int month, int day) { int shifts[] = {0, 3, 3, 6, 1, 4, 6, 2, 5, 0, 3, 5}; int shift = shifts[month - 1]; if (is_leap_year(year) and (month > 2)) { shift += 1; }; year = (year - 1) % 400; int century = year / 100; int index = ((4 * century) + (year % 100)) % 28; int weekday = (index + (index / 4)) + shift + (day - 1); return (weekday % 7); }
Таким образом, можно вычислить день недели для любой даты, зная всего лишь 12 чисел: смещения дней недели на первое число каждого месяца.
