Все мы изучали в курсе математики численные методы. Это такие методы, как интегрирование, интерполяция, ряды и так далее. Существует два вида числовых методов: детерминированные и рандомизированные.
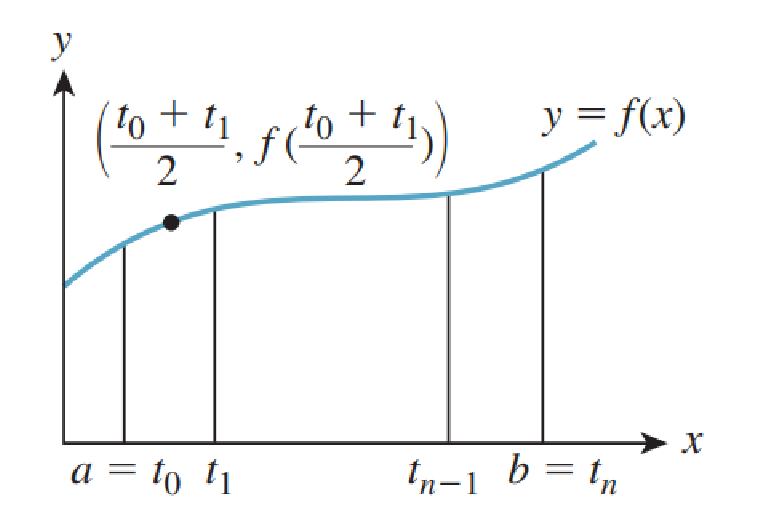
Типичный детерминированный метод интегрирования функции в интервале
в интервале ![$[a, b]$](https://habrastorage.org/getpro/habr/formulas/58b/7f7/be8/58b7f7be8c846796f6af0f80072b3431.svg) выглядит так: мы берём
выглядит так: мы берём  равномерно расположенных в интервале точек
равномерно расположенных в интервале точек  , вычисляем
, вычисляем  в средней точке
в средней точке  каждого из интервалов, определяемых этими точками, суммируем результаты и умножаем на ширину каждого интервала
каждого из интервалов, определяемых этими точками, суммируем результаты и умножаем на ширину каждого интервала  . Для достаточно непрерывных функций
. Для достаточно непрерывных функций  при увеличении
при увеличении  результат будет сходиться к верному значению.
результат будет сходиться к верному значению.
Вероятностный метод, или метод Монте-Карло для вычисления, или, если точнее, приблизительной оценки интеграла в интервале
в интервале ![$[a, b]$](https://habrastorage.org/getpro/habr/formulas/58b/7f7/be8/58b7f7be8c846796f6af0f80072b3431.svg) , выглядит так: пусть
, выглядит так: пусть  — случайно выбранные точки в интервале
— случайно выбранные точки в интервале ![$[a, b]$](https://habrastorage.org/getpro/habr/formulas/58b/7f7/be8/58b7f7be8c846796f6af0f80072b3431.svg) . Тогда
. Тогда  — это случайное значение, среднее которого является интегралом
— это случайное значение, среднее которого является интегралом ![$\int_{[a,b]}f$](https://habrastorage.org/getpro/habr/formulas/205/dab/c57/205dabc57a31af5d7fa9d131d1f87eed.svg) . Для реализации метода мы используем генератор случайных чисел, генерирующий
. Для реализации метода мы используем генератор случайных чисел, генерирующий  точек в интервале
точек в интервале ![$[a, b]$](https://habrastorage.org/getpro/habr/formulas/58b/7f7/be8/58b7f7be8c846796f6af0f80072b3431.svg) , вычисляем в каждой
, вычисляем в каждой  , усредняем результаты и умножаем на
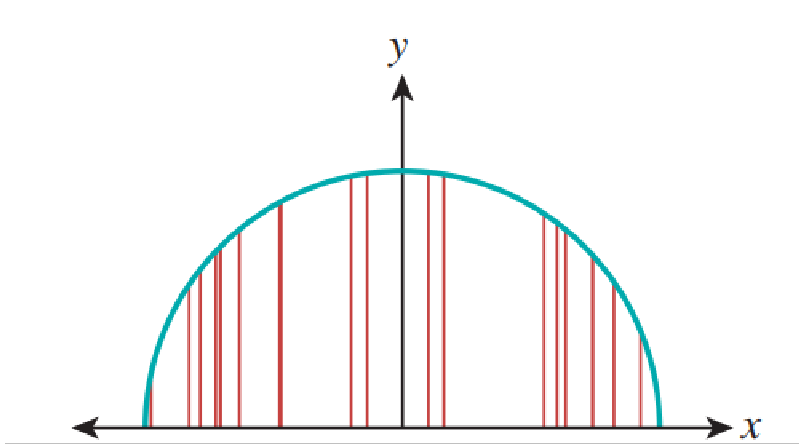
, усредняем результаты и умножаем на  . Это даёт нам приблизительное значение интеграла, как показано на рисунке ниже.
. Это даёт нам приблизительное значение интеграла, как показано на рисунке ниже.  с 20 сэмплами аппроксимирует верный результат, равный
с 20 сэмплами аппроксимирует верный результат, равный  .
.
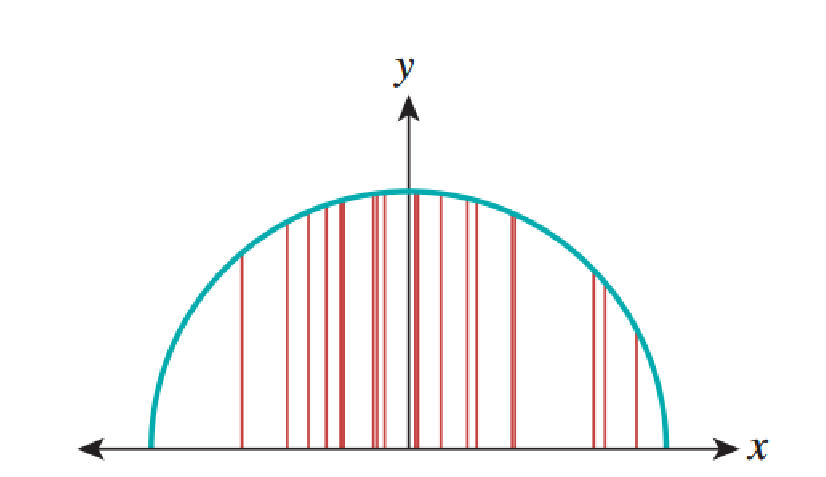
Разумеется, каждый раз, когда мы будем вычислять такое приблизительное значение, то будем получать разный результат. Дисперсия этих значений зависит от формы функции . Если мы генерируем случайные точки
. Если мы генерируем случайные точки  неравномерно, то нам необходимо слегка изменить формулу. Но благодаря использованию неравномерного распределения точек мы получаем огромное преимущество: заставив неравномерное распределение отдавать предпочтение точкам
неравномерно, то нам необходимо слегка изменить формулу. Но благодаря использованию неравномерного распределения точек мы получаем огромное преимущество: заставив неравномерное распределение отдавать предпочтение точкам  , где
, где  велика, мы можем значительно снизить дисперсию приблизительных значений. Такое принцип неравномерной дискретизации называется выборкой по значимости.
велика, мы можем значительно снизить дисперсию приблизительных значений. Такое принцип неравномерной дискретизации называется выборкой по значимости.
Так как за последние десятилетия в методиках рендеринга произошёл масштабный переход от детерминированных к рандомизированным подходам, мы изучим рандомизируемые подходы, применяемые для решения уравнений рендеринга. Для этого мы используем случайные величины, математическое ожидание и дисперсию. Мы имеем дело с дискретными значениями, потому что компьютеры дискретны по своей сути. Непрерывные величины имеют дело с функцией плотности вероятности, но в статье мы не будем её рассматривать. Мы поговорим о функции распределения масс (probability mass function). PMF обладает двумя свойствами:
Первое свойство называется «неотрицательностью». Второе называется «нормальностью». Интуитивно понятно, что представляет собой множество результатов некоторого эксперимента, а
представляет собой множество результатов некоторого эксперимента, а  — это результат вероятности
— это результат вероятности  , член
, член  . Исход — это подмножество пространства вероятностей. Вероятность исхода является суммой PMF элементов этого исхода, поскольку
. Исход — это подмножество пространства вероятностей. Вероятность исхода является суммой PMF элементов этого исхода, поскольку
Случайная переменная — это функция, обычно обозначаемая заглавной буквой, ставящая в соответствие пространству вероятностей вещественные числа:
Учтите, что функция — это не переменная, а функция с вещественными значениями. Она также не является случайной,
— это не переменная, а функция с вещественными значениями. Она также не является случайной,  — это отдельное вещественное число для любого результата
— это отдельное вещественное число для любого результата  .
.
Случайная переменная используется для определения исходов. Например, множество результата , для которого
, для которого  , то есть если ht и th — это множество строк, обозначающих «орлы» или «решки», то
, то есть если ht и th — это множество строк, обозначающих «орлы» или «решки», то
и
это исход с вероятностью . Запишем это как
. Запишем это как  . Мы используем предикат
. Мы используем предикат  как укороченную запись для исхода, определяемого предикатом.
как укороченную запись для исхода, определяемого предикатом.
Давайте взглянем на фрагмент кода, симулирующий эксперимент, описанный представленными выше формулами:
Здесь мы обозначаем как всех возможных выполнений программы, объявив два выполнения одинаковыми значениями, возвращаемыми
всех возможных выполнений программы, объявив два выполнения одинаковыми значениями, возвращаемыми
Теперь аналогия становится понятнее. Множество возможных выполнений программы и связанные с ними вероятности — это пространство вероятностей. Переменные программы, зависящие от вызовов
Давайте обсудим ожидаемое значение, также называемое средним. По сути это сумма произведения PMF и случайной переменной:
Представьте, что h — это «орлы», а t — «решки». Мы уже рассмотрели ht и th. Также существуют hh и tt. Поэтому ожидаемое значение будет следующим:
Вы можете задаться вопросом, откуда взялся . Здесь я имел в виду, что мы должны назначать значение
. Здесь я имел в виду, что мы должны назначать значение  самостоятельно. В данном случае мы присвоили h значение 1, а t значение 0.
самостоятельно. В данном случае мы присвоили h значение 1, а t значение 0.  равно 2, потому что в ней содержится 2
равно 2, потому что в ней содержится 2  .
.
Давайте поговорим о распределении. Распределение вероятностей — это функция, дающая вероятности различных исходов события.
Когда мы говорим, что случайная переменная имеет распределение
имеет распределение  , то должны обозначить
, то должны обозначить  .
.
Рассеяние значений, скопившихся вокруг , называется её дисперсией и определяется следующим образом:
, называется её дисперсией и определяется следующим образом:
Где — это среднее
— это среднее  .
.
 называется стандартным отклонением. Случайные переменные
называется стандартным отклонением. Случайные переменные  и
и  называются независимыми, если:
называются независимыми, если:
Важные свойства независимых случайных переменных:
Когда я начал с рассказа о вероятности, то сравнивал непрерывную и дискретную вероятности. Мы рассмотрели дискретную вероятность. Теперь поговорим о разнице между непрерывной и дискретной вероятностями:
Свойства PDF:
Но если распределение равномерно, то PDF определяется так:
равномерно, то PDF определяется так:

При непрерывной вероятности![$E[X]$](https://habrastorage.org/getpro/habr/formulas/21b/2bd/703/21b2bd703d762fc0d2466eee0869dd6b.svg) определяется следующим образом:
определяется следующим образом:
Теперь сравним определения PMF и PDF:
В случае непрерывной вероятности случайные величины лучше называть случайными точками. Потому что если — пространство вероятностей, а
— пространство вероятностей, а  отображается в другое пространство, отличающееся от
отображается в другое пространство, отличающееся от  , тогда мы должны назвать
, тогда мы должны назвать  случайной точкой, а не случайной величиной. Понятие плотности вероятностей применимо здесь, потому что можно сказать, что для любого
случайной точкой, а не случайной величиной. Понятие плотности вероятностей применимо здесь, потому что можно сказать, что для любого  мы имеем:
мы имеем:

Теперь давайте применим то, что мы узнали, к сфере. Сфера имеет три координаты: широту, д��лготу и дополнение широты. Долготу и дополнение широты мы используем только в , двухмерные декартовы координаты, применённые к случайной величине
, двухмерные декартовы координаты, применённые к случайной величине  , превращают её в
, превращают её в  . Получаем следующую детализацию:
. Получаем следующую детализацию:
Мы начинаем с равномерной плотности вероятностей при
при ![$[0, 1] \times [0, 1]$](https://habrastorage.org/getpro/habr/formulas/3e8/8bc/62f/3e88bc62f3ada3352fbf9237a1d5985e.svg) , или
, или  . Посмотрите выше формулу плотности равномерной вероятности. Для удобства мы запишем
. Посмотрите выше формулу плотности равномерной вероятности. Для удобства мы запишем  .
.
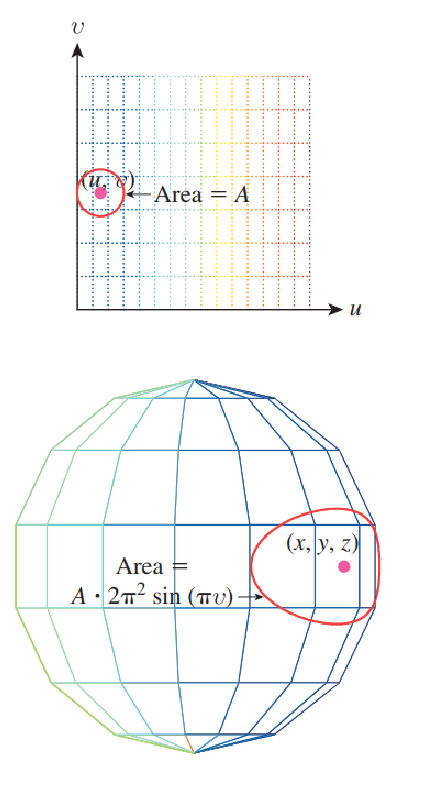
У нас есть интуитивное понимание, что если выбирать точки равномерно и случайно в единичном квадрате и использовать для преобразования их в точки на единичной сфере, то они будут скапливаться рядом с полюсом. Это означает, что полученная плотность вероятностей в
для преобразования их в точки на единичной сфере, то они будут скапливаться рядом с полюсом. Это означает, что полученная плотность вероятностей в  не будет равномерной. Это показано на рисунке ниже.
не будет равномерной. Это показано на рисунке ниже.
Теперь мы обсудим способы приблизительного определения ожидаемого значения непрерывной случайной величины и его применения для определения интегралов. Это важно, потому что в рендеринге нам нужно определять значение интеграла отражающей способности:
для различных значений и
и  . Значение
. Значение  — это направление падающего света. Код, генерирующий случайное число, равномерно распределённое в интервале
— это направление падающего света. Код, генерирующий случайное число, равномерно распределённое в интервале ![$[0, 1]$](https://habrastorage.org/getpro/habr/formulas/a5d/538/f83/a5d538f83bd73f9d1c9e8338db9a398a.svg) и берущий квадратный корень, создаёт значение в интервале от 0 до 1. Если мы используем для него PDF, поскольку это равномерное значение, то ожидаемое значение будет равно
и берущий квадратный корень, создаёт значение в интервале от 0 до 1. Если мы используем для него PDF, поскольку это равномерное значение, то ожидаемое значение будет равно  . Также это значение является средним значением
. Также это значение является средним значением  в этом интервале. Что это означает?
в этом интервале. Что это означает?
Рассмотрим теорему 3.48 из книги «Computer Graphics: Principles and Practice». Она гласит, что если![$f : [a, b] \rightarrow \mathbb{R}$](https://habrastorage.org/getpro/habr/formulas/940/105/624/9401056244e224bbcdb6d3928f64b582.svg) является функцией с вещественными значениями, а
является функцией с вещественными значениями, а  является равномерной случайной величиной в интервале
является равномерной случайной величиной в интервале ![$[a, b]$](https://habrastorage.org/getpro/habr/formulas/58b/7f7/be8/58b7f7be8c846796f6af0f80072b3431.svg) , то
, то  — это случайная величина, ожидаемое значение которой имеет вид:
— это случайная величина, ожидаемое значение которой имеет вид:
Что это нам говорит? Это значит, что можно использовать рандомизированный алгоритм для вычисления значения интеграла, если мы достаточно много раз выполним код и усредним результаты.
В общем случае мы получим некую величину , как в показанном выше интеграле, которую нужно определить, и некий рандомизированный алгоритм, возвращающий приблизительное значение
, как в показанном выше интеграле, которую нужно определить, и некий рандомизированный алгоритм, возвращающий приблизительное значение  . Такая случайная переменная для величины называется эстиматором. Считается, что эстиматор без искажений, если его ожидаемое значение равно
. Такая случайная переменная для величины называется эстиматором. Считается, что эстиматор без искажений, если его ожидаемое значение равно  . В общем случае эстиматоры без искажений предпочтительнее, чем с искажениями.
. В общем случае эстиматоры без искажений предпочтительнее, чем с искажениями.
Мы уже обсудили дискретные и непрерывные вероятности. Но существует и третий тип, который называется смешанными вероятностями и используется в рендеринге. Такие вероятности возникают вследствие импульсов в функциях распределения двунаправленного рассеяния, или импульсов, вызванных точечными источниками освещения. Такие вероятности определены в непрерывном множестве, например, в интервале![$[0, 1]$](https://habrastorage.org/getpro/habr/formulas/a5d/538/f83/a5d538f83bd73f9d1c9e8338db9a398a.svg) , но не определены строго функцией PDF. Рассмотрим такую программу:
, но не определены строго функцией PDF. Рассмотрим такую программу:
В шестидесяти процентах случаев программа будет возвращать 0.3, а в оставшихся 40% она будет возвращать значение, равномерно распределённое в![$[0, 1]$](https://habrastorage.org/getpro/habr/formulas/a5d/538/f83/a5d538f83bd73f9d1c9e8338db9a398a.svg) . Возвращаемое значение — это случайная переменная, имеющая при 0.3 массу вероятности 0.6, а его PDF во всех других точках задаётся как
. Возвращаемое значение — это случайная переменная, имеющая при 0.3 массу вероятности 0.6, а его PDF во всех других точках задаётся как  . Мы должны определить PDF как:
. Мы должны определить PDF как:

В целом, случайная переменная со смешанной вероятностью — это такая переменная, для которой существует конечное множество точек в области определения PDF, и наоборот, равномерно распределённые точки, где PMF не определена.
Типичный детерминированный метод интегрирования функции

Вероятностный метод, или метод Монте-Карло для вычисления, или, если точнее, приблизительной оценки интеграла

Разумеется, каждый раз, когда мы будем вычислять такое приблизительное значение, то будем получать разный результат. Дисперсия этих значений зависит от формы функции

Так как за последние десятилетия в методиках рендеринга произошёл масштабный переход от детерминированных к рандомизированным подходам, мы изучим рандомизируемые подходы, применяемые для решения уравнений рендеринга. Для этого мы используем случайные величины, математическое ожидание и дисперсию. Мы имеем дело с дискретными значениями, потому что компьютеры дискретны по своей сути. Непрерывные величины имеют дело с функцией плотности вероятности, но в статье мы не будем её рассматривать. Мы поговорим о функции распределения масс (probability mass function). PMF обладает двумя свойствами:
- Для каждого
существует
.
Первое свойство называется «неотрицательностью». Второе называется «нормальностью». Интуитивно понятно, что
Случайная переменная — это функция, обычно обозначаемая заглавной буквой, ставящая в соответствие пространству вероятностей вещественные числа:
Учтите, что функция
Случайная переменная используется для определения исходов. Например, множество результата
и
это исход с вероятностью
Давайте взглянем на фрагмент кода, симулирующий эксперимент, описанный представленными выше формулами:
headcount = 0
if (randb()): // first coin flip
headcount++
if (randb()): // second coin flip
headcount++
return headcountЗдесь мы обозначаем как
ranb() булеву функцию, которая возвращает true в половине случаев. Как она связана с нашей абстракцией? Представьте множество ranb, попарно идентичными. Это значит, что существует четыре возможных выполнений программы, в которых два вызова ranb() возвращают TT, TF, FT и FF. По своему опыту мы можем сказать, что эти четыре выполнения равновероятны, то есть каждое встречается примерно в четверти случаев.Теперь аналогия становится понятнее. Множество возможных выполнений программы и связанные с ними вероятности — это пространство вероятностей. Переменные программы, зависящие от вызовов
ranb, — это случайные переменные. Надеюсь, теперь вам всё понятно.Давайте обсудим ожидаемое значение, также называемое средним. По сути это сумма произведения PMF и случайной переменной:
Представьте, что h — это «орлы», а t — «решки». Мы уже рассмотрели ht и th. Также существуют hh и tt. Поэтому ожидаемое значение будет следующим:
Вы можете задаться вопросом, откуда взялся
Давайте поговорим о распределении. Распределение вероятностей — это функция, дающая вероятности различных исходов события.
Когда мы говорим, что случайная переменная
Рассеяние значений, скопившихся вокруг
Где
Важные свойства независимых случайных переменных:
Когда я начал с рассказа о вероятности, то сравнивал непрерывную и дискретную вероятности. Мы рассмотрели дискретную вероятность. Теперь поговорим о разнице между непрерывной и дискретной вероятностями:
- Значения непрерывны. То есть числа бесконечны.
- Некоторые аспекты анализа требуют таких математических тонкостей, как измеряемость.
- Наше пространство вероятностей будет бесконечным. Вместо PMF мы должны использовать функцию плотности вероятностей (PDF).
Свойства PDF:
- Для каждого
у нас есть
Но если распределение
При непрерывной вероятности
Теперь сравним определения PMF и PDF:
В случае непрерывной вероятности случайные величины лучше называть случайными точками. Потому что если
Теперь давайте применим то, что мы узнали, к сфере. Сфера имеет три координаты: широту, д��лготу и дополнение широты. Долготу и дополнение широты мы используем только в
Мы начинаем с равномерной плотности вероятностей
У нас есть интуитивное понимание, что если выбирать точки равномерно и случайно в единичном квадрате и использовать

Теперь мы обсудим способы приблизительного определения ожидаемого значения непрерывной случайной величины и его применения для определения интегралов. Это важно, потому что в рендеринге нам нужно определять значение интеграла отражающей способности:
для различных значений
Рассмотрим теорему 3.48 из книги «Computer Graphics: Principles and Practice». Она гласит, что если
Что это нам говорит? Это значит, что можно использовать рандомизированный алгоритм для вычисления значения интеграла, если мы достаточно много раз выполним код и усредним результаты.
В общем случае мы получим некую величину
Мы уже обсудили дискретные и непрерывные вероятности. Но существует и третий тип, который называется смешанными вероятностями и используется в рендеринге. Такие вероятности возникают вследствие импульсов в функциях распределения двунаправленного рассеяния, или импульсов, вызванных точечными источниками освещения. Такие вероятности определены в непрерывном множестве, например, в интервале
if uniform(0, 1) > 0.6 :
return 0.3
else :
return uniform(0, 1)В шестидесяти процентах случаев программа будет возвращать 0.3, а в оставшихся 40% она будет возвращать значение, равномерно распределённое в
В целом, случайная переменная со смешанной вероятностью — это такая переменная, для которой существует конечное множество точек в области определения PDF, и наоборот, равномерно распределённые точки, где PMF не определена.
