Хабр Курсы для всех
РЕКЛАМА
Практикум, Хекслет, SkyPro, авторские курсы — собрали всех и попросили скидки. Осталось выбрать!

Свойство. Потенциальная разделяющая ось будет находиться в следующих множествах:
- Нормы плоскостей каждого куба(красные)
- Векторное произведение ребер кубов {[x,y]: x∈X, y∈Y}
где X — ребра первого куба (зеленые), а Y — второго (синие).
мы должны условно «проверить» все проекции касательных к кругу, с бесконечно малым шагом. Для трёхмерного случая, надо будет делать это дважды: сначала плоскости к сфере, а потом касательные к кругу вокруг двумерной проекции.
Не увидел в 3 и 4 актах, почему бесконечности заменены на какие-то оси кандидаты их будет достаточно.
Как справляется ваш алгоритм с таким случаем?

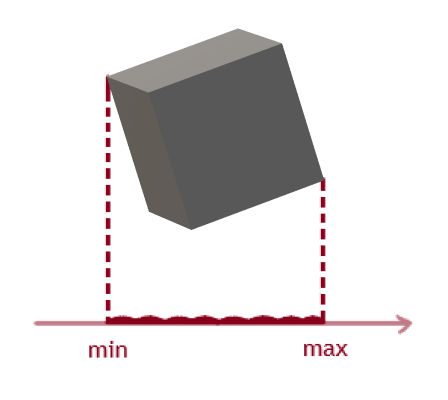
почему на иллюстрациях разделяющие оси не параллельны граням.
Верно, но у нас векторное произведение [x,y], в котором X и Y разные множества(посмотрите внимательно).
Т.е. x — ребро первого куба, а y — второго
Если будет сфера с объектом, то рассматриваем в качестве осей нормали второго объекта. Если две сферы, то проверяем радиусами и расстоянием.
Как я говорил в другом комментарии — для примитивов нецелесообразно применять общий подход реализации этой теоремы
Свойство. Потенциальная разделяющая ось будет находиться в следующих множествах:
Нормы плоскостей каждого куба(красные)
Векторное произведение ребер кубов,
где X — ребра первого куба (зеленые), а Y — второго (синие).
Нормы плоскостей каждого куба(красные)
Векторное произведение ребер кубов
Координаты центра куба
Размеры куба (высота, ширина, глубина)
Кватернион куба
Для меня невероятно тяжело было объяснить как это работает
Моей целью было поделиться своим опытом в решение задач связанных с определением пересечений двух выпуклых объектов. А так же доступно и понятно рассказать о данной теореме.
Не будем заострять внимание на том, что пункта два…
Вы серьёзно?! Да я выкинул весь этот обзац сразу как только понял, что это частный случай не имеющий никакого отношения к габаритным размерам (что могло бы помочь сократить количество кандидатов), либо к общей теории.
Моё личное мнение: вы сделали всё, что бы увести читателя в сторону и не объяснить ничего, кроме того, что вы сами умете писать программы и делать какие-то вычисления: картинки ничего не имеющие с реальностью, нелепая терминология, куски кода вместо объяснений, какие-то частные примеры примитивнейших вещей до которых нельзя опускаться если говоришь о теории.
Я с самого начало указал, что будут рассматриваться случай с кубами, но идея с более полигональными объектами будет сохранена.
Обнаружение столкновений и теорема о разделяющей оси