Вместо вступления
Статья содержит пример ручной оптимизации критического участка прикладной программы применительно к бюджетным микроконтроллерам stm32, повышающий производительность в 5 и более раз по сравнению с библиотечной функцией.
В прикладных программах часто требуется извлечение квадратного корня. Функция sqrt включена в стандартную библиотеку языка С и оперирует действительными числами:
double sqrt (double num); long double sqrtl (long double num);
Бюджетные микроконтроллеры работают, преимущественно, с целыми числами; регистров для обработки действительных чисел у них, как правило, нет.
В этих условиях целочисленное извлечение квадратного корня сопровождается не только высокими вычислительными затратами, но и потерей точности — Пример 1.
Пример 1: Потеря точности в прямом и обратном преобразованиях
// исходные значения uint32_t L1 = 169; uint32_t L2 = 168; // прямое преобразование uint32_t r1 = ( uint32_t )sqrt( ( double ) L1 ); uint32_t r2 = ( uint32_t )sqrt( ( double ) L2 ); // обратное преобразование L1 = r1*r1; // r1 = 13 L2 = r2*r2; // r2 = 12 // результат преобразований // L1 = 169 — было 169 // L2 = 144 — было 168, ошибка двойного преобразования 14%
Постановка задачи
Поднять точность целочисленных вычислений sqrt через округление до ближайшего целого.
По возможности, увеличить производительность.
Решение задачи
Написать несколько функций-кандидатов для извлечения квадратного корня на основе разных алгоритмов.
Выбрать лучший из них, сравнивая на соответствие поставленной задаче.
Первая функция-кандидат создаётся на основе стандартной библиотеки. Далее именуем её "sqrt_fpu" — Пример 2.
Пример 2: Расчёт целочисленного корня алгоритмом sqrt_fpu
uint16_t sqrt_fpu ( uint32_t L ) { if ( L < 2 ) return ( uint16_t ) L; double f_rslt = sqrt( ( double ) L ); uint32_t rslt = ( uint32_t ) f_rslt; if ( !( f_rslt - ( double ) rslt < .5 ) ) rslt++; return ( uint16_t ) rslt; }
Достоинства sqrt_fpu:
- решена задача округления результата до ближайшего целого.
Недостатки sqrt_fpu:
- потеря производительности через применение операций с плавающей точкой при отсутствии FPU;
- сомнительный потенциал оптимизации из-за вызова библиотечной функции.
Принимаем sqrt_fpu за эталон.
Функция-кандидат №2 интересна уже на уровне описания алгоритма:
«Квадратный корень из целого равен количеству возрастающих положительных нечётных чисел, вычитаемых последовательно из целого числа, начиная с единицы, до достижения нуля.»
Именуем далее этот алгоритм "sqrt_odd" — Пример 3.
Пример 3: Расчёт целочисленного корня алгоритмом sqrt_odd
uint16_t sqrt_odd ( uint32_t L ) { if ( L < 2 ) return ( uint16_t ) L; uint16_t div = 1, rslt = 1; while ( 1 ) { div += 2; if ( ( uint32_t ) div >= L ) return rslt; L -= div, rslt++; } }
Алгоритм возвращает квадратный корень, округлённый отбрасыванием
дробной части.
Достоинства sqrt_odd:
- компактный код;
Недостатки sqrt_odd:
- отбрасывание дробной части вместо округления;
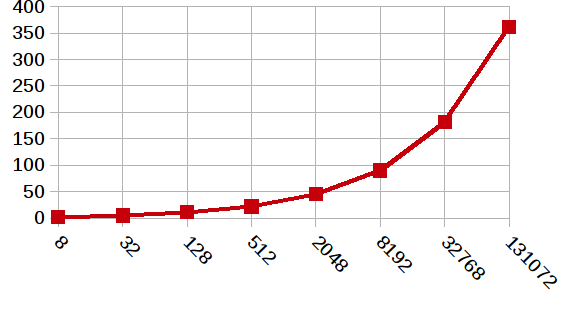
- экспоненциальная зависимость вычислительных затрат от аргумента; 150 циклов и более в диапазоне 1E+4+ — Иллюстрация 1;
- отсутствие очевидных путей алгоритмической оптимизации.
Иллюстрация 1: Зависимость числа итераций sqrt_odd от аргумента
Функция-кандидат №3. Приближённое вычисление квадратного корня методом Ньютона:
«Корень из числа равен половине суммы приближённого корня и частного числа с приближённым корнем»:
Rj = ( N / Ri + Ri ) / 2
Назовём простую модернизацию метода Нютона для целых чисел условно "sqrt_new" — Пример 4.
Пример 4: Расчёт целочисленного корня алгоритмом sqrt_new
uint16_t sqrt_new ( uint32_t L ) { if ( L < 2 ) return ( uint16_t ) L; uint32_t rslt, div; rslt = L; div = L / 2; while ( 1 ) { div = ( L / div + div ) / 2; if ( rslt > div ) rslt = div; else return ( uint16_t ) rslt; } }
Достоинства sqrt_new:
- превосходство в скорости счёта эталона sqrt_fpu и кандидата №2 sqrt_odd, как минимум, в четыре раза;
Недостатки sqrt_new:
- отбрасывание дробной части вместо округления;
Профилирование sqrt_new демонстрирует (Иллюстрация 2):
- практически линейную зависимость числа итераций от аргумента;
- нормальное распределение числа итераций внутри под диапазонов аргумента.
Иллюстрация 2: Зависимость итераций sqtr_new от аргумента (!)
(!) — Вычисления результата в диапазоне 10e5+ требуют 8 и более циклов.
Алгоритм sqrt_new оптимизируется обычным способом:
- уменьшение числа итераций через подбор начального значения делителя до начала цикла;
- отказ, по-возможности, от математических операторов в пользу битовых;
- учёт младшего бита (округление) в целочисленных арифметических вычислениях.
Итоговый алгоритм на основе функции-кандидата №3 будем называть "sqrt_evn" (Пример 5).
Функция sqrt_evn принимает целое без знака и возвращает целочисленный квадратный корень, округлённый до ближайшего целого.
В среднем sqrt_evn затрачивает от 2-х до 5-и циклов на вычисление одного квадратного корня на всём множестве значений аргумента [ 0… 0xFFFFFFFF ], опережая sqrt_new приблизительно на 40%.
В наиболее "употребимом" диапазоне значений [ 1… 10 000 000 ] sqtr_evn вычисляет квадратный корень в среднем за 2-3 цикла.
Наблюдается близкая к линейной зависимость числа итераций sqrt_evn от значения аргумента — Иллюстрация 3.
Иллюстрация 3: Зависимость числа итераций sqtr_evn от аргумента
Собственно, исходный текст алгоритма sqrt_evn — Пример 5.
Пример 5: Модифицированный алгоритм по методу Ньютона sqrt_evn
uint16_t sqrt_evn ( uint32_t L ) { if ( L < 2 ) return ( uint16_t ) L; uint32_t div; uint32_t rslt; uint32_t temp; if ( L & 0xFFFF0000L ) if ( L & 0xFF000000L ) if ( L & 0xF0000000L ) if ( L & 0xE0000000L ) div = 43771; else div = 22250; else if ( L & 0x0C000000L ) div = 11310; else div = 5749; else if ( L & 0x00F00000L ) if ( L & 0x00C00000L ) div = 2923; else div = 1486; else if ( L & 0x000C0000L ) div = 755; else div = 384; else if ( L & 0xFF00L ) if ( L & 0xF000L ) if ( L & 0xC000L ) div = 195; else div = 99; else if ( L & 0x0C00L ) div = 50; else div = 25; else if ( L & 0xF0L ) if ( L & 0x80L ) div = 13; else div = 7; else div = 3; rslt = L; while ( 1 ) { temp = L / div; temp += div; div = temp >> 1; div += temp & 1; if ( rslt > div ) rslt = div; else { if ( L / rslt == rslt - 1 && L % rslt == 0 ) rslt--; return ( uint16_t ) rslt; } } }
В цикле повторяется всего одна «тяжёлая» операция — деление:
{ temp = L / div;… }.
Другие операторы в цикле выполняются в среднем за 1 такт.
Область определения аргумента функции делится на под диапазоны. Для каждого из ни�� устанавливается оптимальный начальный делитель.
Блок условных операторов до начала цикла, задающий начальное значение делителя для каждого под диапазона, слабо влияет на производительность sqrt_evn.
Уменьшение вложенности блока { if } сдвигает разброс числа итераций в диапазонах значений аргумента в большую сторону, увеличивая среднее время вычисления квадратного корня (Иллюстрация 2).
Критерий подбора делителя — минимизация итераций на множестве значений аргумента.
Выбор начальных значений делителя.
Четыре младшие константы [ 3, 7, 13, 25 ] подобраны «на глазок». Далее найдена аппроксимирующая функция (экспонента). Остальные определены по аппроксимирующей формуле.
Погрешности определения начального значения делителя компенсируются сдвигом границ подмножеств значений аргумента — битовые маски в условных операторах.
Сравнительное тестирование алгоритмов
Испытательный стенд:
- Оборудование: STM32F0308-DISCO, на базе MCU STM32F030R8T6
- Сборочная среда: STM32CubeIDE
- Вывод: на терминал рабочей станции через USB-UART PL2303HX
Параметры стенда:
- Начальная настройка оборудования: по умолчанию
- Частота тактирования: CPU — 48 MHz, UART (RS485) — 9600 bit/s
- Профиль сборки: стандартный, Release
- Дополнительные ключи: MCU GCC Linker: Miscellaneous: -u _printf_float
Сравнивались алгоритмы sqrt_fpu, sqrt_new и sqrt_evn.
В процессе теста каждый алгоритм производил 100 000 вычислений квадратного корня в 3-х диапазонах значений аргумента — Иллюстрация 4.
Иллюстрация 4: Процесс тестирования
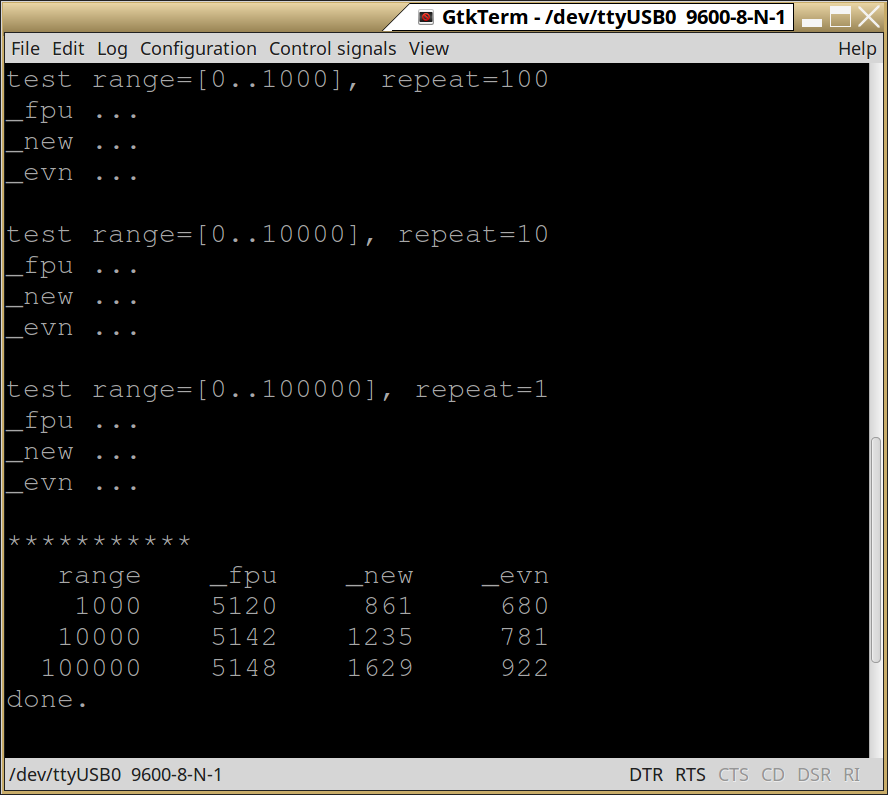
В результирующей таблице затраченное на тест время в миллисекундах.
Стабильность — главное преимущество sqrt_fpu, показавшего слабую зависимость от значения аргумента. Одним словом — эталон.
Графики ниже демонстрируют то же самое, что и скриншот (Иллюстрация 4), но в более наглядном виде.
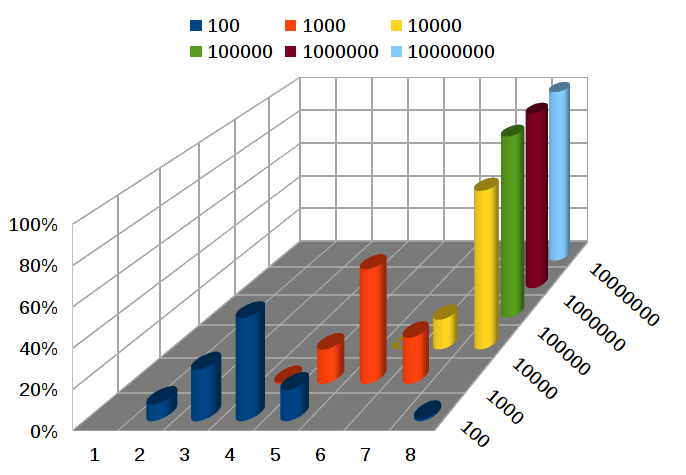
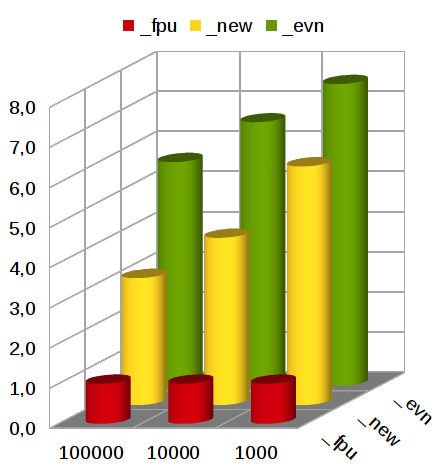
Качественное сравнение (Иллюстрация 5) показывает во сколько раз одни алгоритмы быстрее других.
Иллюстрация 5: Качественное сравнение алгоритмов
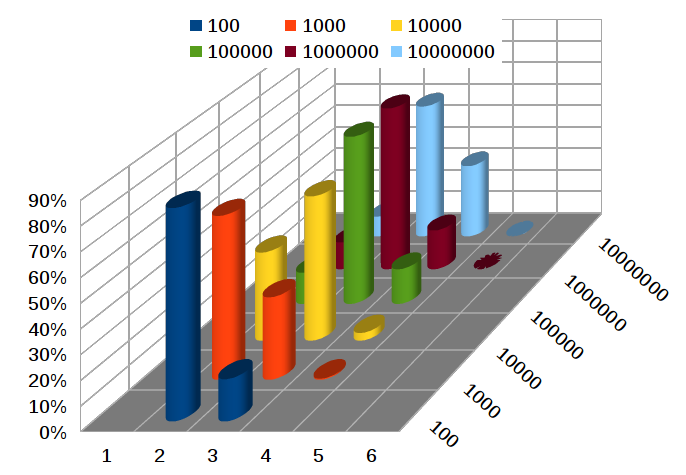
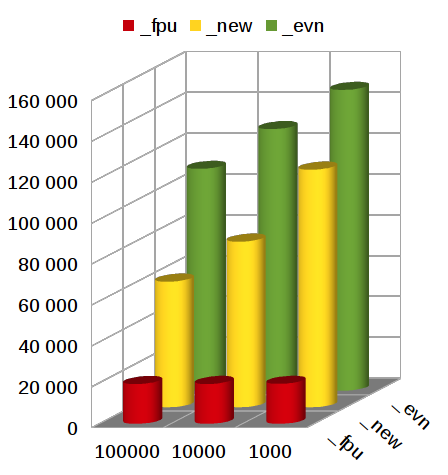
Количественное сравнение (Иллюстрация 6) демонстрирует различие производительности, выраженное в результатах за 1 секунду.
За одну секунду sqrt_fpu вычисляет 19 531, а sqrt_evn 147 059 квадратных корней; sqrt_evn в ~7,5 раз быстрее, чем sqrt_fpu.
Иллюстрация 6: Количественное сравнение алгоритмов
Вместо заключения
Существует много эффективных способов повышения производительности прикладных программ, например, применение старших моделей чипов, содержащих модуль FPU для действительных чисел.
В то же время, ручная алгоритмическая оптимизация кода может оказаться эффективной при массовом производстве мелких IoT, за счёт применения бюджетных моделей микроконтроллеров, освобождая для старших моделей пространство сложных задач.
