Введение

При моделировании систем управления движением роботов требуется решать задачи кинематики и динамики для их исполнительных механизмов. Существует обратная и прямая задача кинематики. Прямая задача кинематики состоит в определении пространственного положения и ориентации характерной точки, как правило, рабочего инструмента манипулятора робота по известным значениям обобщенных координат. Обратная задача кинематики, как и прямая задача, является одной из основных задач кинематического анализа и синтеза. Для управления положением звеньев и ориентацией рабочего инструмента манипулятора возникает необходимость решения обратной задачи кинематики.

Большинство аналитических подходов для решения обратной задачи кинематики являются достаточно затратными с точки зрения вычислительных процедур. Одним из альтернативных подходов является использование нейронных сетей. Входные данные. Рассмотрим трехзвенный манипулятор с параметрами, приведенными в таблице 1.

A

Alfa

D

Tetta

0

pi/2

0.2

0

0.4

0

0

0

0.4

0

0

0

Таблица 1 - параметры DH для трехзвенного манипулятора

В среде MatLab, с использованием свободно распространяемого Robotics Toolbox строится компьютерная модель трехзвенного манипулятора. Ниже приведен фрагмент скрипта MatLab в котором присваиваем в массив ‘L’ значение параметров, A, Alfa, и D из таблицы 1. Для нашей модели - это постоянные значения и в процессе работы с манипулятором они не изменяются. Параметр Tetta мы присваиваем в переменную ‘initialPose_left’-начальное положение нашего манипулятора. 

function [L,initialPose_left,baseL] =model3z 
% Левая рука 
initialPose_left = deg2rad([0 0 0]); 
L(1) = Revolute('d', 0.2, 'alpha', pi/2, 'qlim', initialPose_left(1)+deg2rad([-90 +90]) ); 
L(2) = Revolute('d', 0, 'alpha', 0, 'a', 0.4, 'qlim', initialPose_left(2)+deg2rad([-20 +90]));   
L(3) = Revolute('d', 0, 'alpha', 0, 'a', 0.4, 'qlim', initialPose_left(2)+deg2rad([-90 +90])); 
% -178 +178 
baseL = [1 0 0 0;  
        0 1 0 0;  
        0 0 1 0;  
        0 0 0 1];

На рисунке 1 приведено графическое отображение выбранного (см. таблицу 1) начального положения трёхзвенного манипулятора. 

Рисунок 1- Графическое отображение выбранного начального положения трёхзвенного манипулятора
Рисунок 1- Графическое отображение выбранного начального положения трёхзвенного манипулятора

Изменяя значение углов Tetta, мы можем задавать произвольное начальное положение манипулятора. Для того чтобы манипулятор изначально имел другое положение необходимо изменить переменную initialPose_left. 

Входные данные

На входные данные нейронной сети подается положение и ориентация конечного узла манипулятора. Задача нейронной сети спрогнозировать конфигурацию соединения узлов манипулятора, которые максимально будут соответствовать заданному положению и ориентации в пространстве. 

Суть метода заключается в случайном выборе заведомо известных положений манипулятора и нахождения с помощью решения прямой задачи кинематики, координат и ориентации в пространстве конечной точки.  

Для обучающихся данных были созданы известные положения сервоприводов робота в случайном порядке. Полученные данные будем сохранять в виде вектора:

Y_i=[q_1,q_2,q_3...q_n],

где q – это угол поворота сервопривода каждого сочленения. 

%Получаем минимальное и максимальное возможное положение сервоприводов 
t1_min = L(1).qlim(1); t1_max = L(1).qlim(2);  
t2_min = L(2).qlim(1); t2_max = L(2).qlim(2); 
t3_min = L(3).qlim(1); t3_max = L(3).qlim(2); 
% массив случайных положений сервоприводов 
t1 = t1_min + (t1_max-t1_min)*rand(N,1); 
t2 = t2_min + (t2_max-t2_min)*rand(N,1); 
t3 = t3_min + (t3_max-t3_min)*rand(N,1); 
Y = horzcat(t1, t2, t3);

Решая прямую задачу кинематики, были получены для каждого угла сервопривода координаты конечной точки манипулятора. Полученные значения сохраняются в векторе: 

X_i=[x,y,z,R], R=[φ,θ,γ]

Где:  x,y,z – координаты в пространстве конечной точки манипулятора. R –матрица поворота, представленная через углы Эйлера. 

% массив матриц преобразований 4x4 
T = zeros(4, 4, N); 
T(:, :, :) = leftArm.fkine(Y); % прямая задача, получаем координаты положения по углам сервопривода 
%R = tr2rpy(T(1:3, 1:3, :), 'arm'); % получаем тангаж рыскание и крен 
R = tr2eul(T(1:3, 1:3, :)); % получаем тангаж рыскание и крен 
Tx = reshape(T(1, 4, :), [N 1]); % все Х-ы 
Ty = reshape(T(2, 4, :), [N 1]); 
Tz = reshape(T(3, 4, :), [N 1]); 
% scatter3(Tx,Ty,Tz,'.','r'); 
X = horzcat(Tx, Ty, Tz, R); % массив координат

Собранные данные будем подавать на вход нейронной сети. На Рисунке 2 показано начальное положение трехзвенного манипулятора, точками отмечено конечное положение манипулятора для 3000 случайно сгенерированных наборов значений углов соединения. 

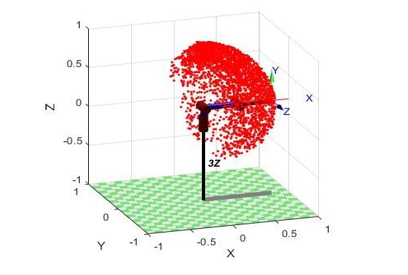
Рисунок 2 - начальное положение трехзвенного манипулятора, точками отмечено конечное положение манипулятора
Рисунок 2 - начальное положение трехзвенного манипулятора, точками отмечено конечное положение манипулятора

Итого, был получен набор для обучения из 3000 данных. В качестве входящих значений для обучения нейронной сети мы имеем две матрицы, состоящие из набора векторов X и Y. 

Для более точного решения задачи, на вход нейронной сети должны подаваться только уникальные данные поэтому дубликаты входных данных должны быть удалены.

Нейронная сеть

Для создания нейронной ��ети будет использоваться библиотека Keras для Python. В начале набор разбивается на тренировочные и тестовые данные. 

X_train, X_test, y_train, y_test = train_test_split(data_x, data_y, test_size=0.2,
random_state=42)

Новая сеть обучается «с нуля» в течение пятиста эпох и затем оценивается получившийся результат на тестовых данных. Ниже приведен фрагмент кода. 

def base_model():
 model = Sequential()
 model.add(Dense(32,input_dim=6,activation='relu'))
 model.add(Dense(64,activation='relu'))
 model.add(Dense(128,activation='relu'))
 model.add(Dense(32,activation='relu'))
 model.add(Dense(3, init='normal'))
 model.compile(loss='mean_absolute_error', optimizer = 'adam', metrics=['accuracy'])
 model.summary()
 return model

Трехзвенный манипулятор имеет небольшую степень свободы, для решения этой задачи может справиться небольшая нейронная сеть. Рациональней использовать нейронную сеть с пятью слоями. Можно построить такую же сеть и на одном слое, но количество нейронов во внутреннем слое сильно возрастет, что приведет к замедлению обучения. Поэтому вариант сети с большим количеством, скрытых слоев, может оказаться гораздо экономней. Теперь обучим новую сеть нуля в течение пятиста эпох используя оболочку KerasRegressor, которая встроенная в Keras.

clf = KerasRegressor(build_fn=base_model, epochs=500, batch_size=20,verbose=2)
clf.fit(X_train,y_train)

После обучения сети ее можно использовать для прогнозирования. 

res = clf.predict(X_test)

Модель показала на тестовом наборе 99% точности, что является хорошим результатом. 

Результат обучения

На Рисунке 3 линией отмечено движение робота, рассчитанное обратной кинематикой, точками отмечены положение робота, найденное нейронной сетью. Как видно траектории ча��тично совпали. В ходе численного моделирования была проведена серия экспериментов, различающихся в зависимости от выборки и количества эпох обучения. Многочисленные эксперименты показали высокую эффективность предложенного метода моделирования нейронной сети для обратной кинематической задачи. Основная проблема нейронных сетей - нехватка памяти. Также в алгоритм адаптивных нейронных сетей, в которых нет памяти, нет возможность вспомнить предыдущие ситуации, чтобы улучшить свою работу, когда снова столкнулся с такой же ситуацией.

%% Проверка решений нейронной сети, движение по кругу 
M=[-178:10:178]; % массив изменений первого узла от -178 градусов до +178 градусов с шагом 10 
M_size=length(M); 
first_q=zeros(M_size, 3); 
T33 = zeros(4, 4, M_size); 
T34 = zeros(4, 4, M_size); 
first_q(:,1)=[deg2rad(M)]; % подготавливаем q 
T33(:, :, :) = leftArm.fkine(first_q);% получаем координаты куда должен прийти робот, круговое движение 
R = tr2rpy(T33(1:3, 1:3, :), 'arm'); % получаем тангаж рыскание и крен 
Tx = reshape(T33(1, 4, :), [M_size 1]); % все Х-ы 
Ty = reshape(T33(2, 4, :), [M_size 1]); 
Tz = reshape(T33(3, 4, :), [M_size 1]); 
plot3(Tx,Ty,Tz) 
axis([-1 1 -1 1 -1 1]);hold on;grid on; 

XX = horzcat(Tx, Ty, Tz, R); % массив координат в формате для нейронной сети 
T34(:, :, :) = leftArm.fkine(q_new); % по результатам решений нейронной сети, получаем координаты 
Tx2 = reshape(T34(1, 4, :), [M_size 1]); % все Х-ы 
Ty2 = reshape(T34(2, 4, :), [M_size 1]); 
Tz2 = reshape(T34(3, 4, :), [M_size 1]); 
plot3(Tx2,Ty2,Tz2,'.') 
axis([-1 1 -1 1 -1 1])
Рисунок 3 – Результат прогнозирования
Рисунок 3 – Результат прогнозирования

Заключение

В ходе выполнения работы была реш��на обратная задача кинематики с помощью нейросетевого подхода. Задача была решена для трехзвенного манипулятора. С увеличением числа звеньев, задача резко усложняется из-за возможности возникновения множества решений. С этой целью, в дальнейшем нейронная сеть будет усовершенствована. Входные данные для обучения нейронной сети можно решать несколькими способами. Как с использованием подхода «Programming by demonstration», так и с помощью решения прямой задачи кинематики. В настоящей работе решение прямой задачи кинематики реализовывалось с помощью пакета Matlab и компьютерной модели манипулятора, построенной на основе подхода Денавита – Хартенберга.

Исходники: GitHub