О чём пост?
Данный материал представляет краткое описание проблемы в теории цифровых автоматов и объясняет один из способов решения данной проблемы, который был найден при попытке автоматизации процесса построения цифрововых автоматов.
Введение
Автомат – система механизмов, устройств, в которой полностью автоматизированы процессы получения, преобразования, передачи энергии, материалов, информации.
Термин <<автомат>> в основном используется в двух аспектах:
техническом;
математическом.
При математическом подходе под автоматом понимается математическая модель, у которой должны быть входы, внутренние состояния и выходы. Детали структуры устройства не учитываюся и не рассматриваются.
В техническом подходе под автоматом понимается вполне реальное устройство, например, телефонный автомат, торговый автомат и т. д. В данном случае, естественно, известными являются детали внутреннего строения устройства.
С точки зрения сигналов цифровой автомат (ЦА) – система, которая может принимать входные сигналы, под их воздействием переходить из одного состояния в другое, сохранять его до прихода следующего входного сигнала, выдавать выходные сигналы.
В данной работе рассматриваются цифровые сигналы и двоичная логика на базе логических элементов.

Применение
Теория автоматов лежит в основе всех цифровых технологий и программного обеспечения. Часть математического аппарата теории автоматов напрямую применяется при разработке лексических и синтаксических анализаторов для формальных языков, в том числе языков программирования, а также при построении компиляторов и разработке самих языков программирования, описания аппаратуры, а также разметки.
Другое важнейшее применение теории автоматов — математически строгое нахождение разрешимости и сложности задач.
А��томаты Мура и Мили широко применяются при проектировании цифровых устройств на основе программируемых логических интегральных схем (ПЛИС). Наличие минимальной выходной задержки, связанной с переключением выходного регистра, отсутствие нестабильности переходного процесса на выходе автомата, отсутствие сквозного распространения сигнала через комбинационную схему от входа до выхода автомата, простота описания на языках описания аппаратуры делает автомат Мура практически незаменимым. Также автоматы Мура и взаимодействующие автоматы Мили используются в генетическом программировании.
Описание проблемы
Построение цифрового автомата -- довольно трудоёмкий процесс. Можно выделить следующие этапы разработки ЦА:
1) Очень часто разработка ЦА начинается с реализации графа, который отражает закладываемую логику в простом и понятном для человека виде.
2) Оптимизация графа -- с этой задачей человек может справиться довольно быстро.
3) Определение разрядности памяти. Минимальное число триггеров можно вычислить по формуле:
где, S -- это число состояний, ceil -- функция приведения значения до ближайшего целого числа, которое не меньше исходного.
4) Присвоение состояниям кодов. Алгоритма для правильного задания кодов для состояний нет. Именно от этого зависит сложность уравнений, которые мы получим для входов триггеров и количество элементов необходимых для сборки схемы.
5) Составление таблицы состояний-переходов.
6) Составление булевых арифметических уравнений для входов триггеров. Карты Карно составляются по таблице состояний-переходов, уравнения минимизируются.
7) Преобразование уравнений для согласования с элементной базой.
8) Разработка электрической схемы.
Основная проблема -- отсутствие алгоритма для задания кодов состояниям автомата таким образом, чтобы уравнения для входов триггеров были как можно проще.
Решение
Была разработана программа для построения цифровых автоматов. На вход программа принимает граф. В программе граф представляется в наборе вершин и рёбер(вершина, входной сигнал, вершина для перехода). Итерируясь по рёбрам составляются таблицы истинности для каждого разряда в СКНФ и СДНФ. Методом Куайна-Мак-Класки минимизируются обе формы уравнений. Для каждого разряда выбирается выражение с минимальным количеством логических операций <<И>>, <<ИЛИ>>. Общее количество этих операций является критерием качества данной кодировки.
Количество возможных вариантов задания состояний можно рассчитать зная разрядность памяти(M) и количество состояний(S).
Количество кодов:
Количество вариантов выборки(V) нужного количества состояний(S) из всего количества кодов(C), формула из комбинаторики:
Количество возможных вариантов задания состояний(A) равно:
Если перебирать все варианты и потом отобрать лучший, то в зависимости от графа программа может исполняться слишком долго. Такой вариант подойдёт для автоматов с небольшим числом вариантов задания кодов состояний.
Для автоматов с большим числом возможных вариантов задания состояний был разработан генетический алгоритм перебора вариантов состояний.
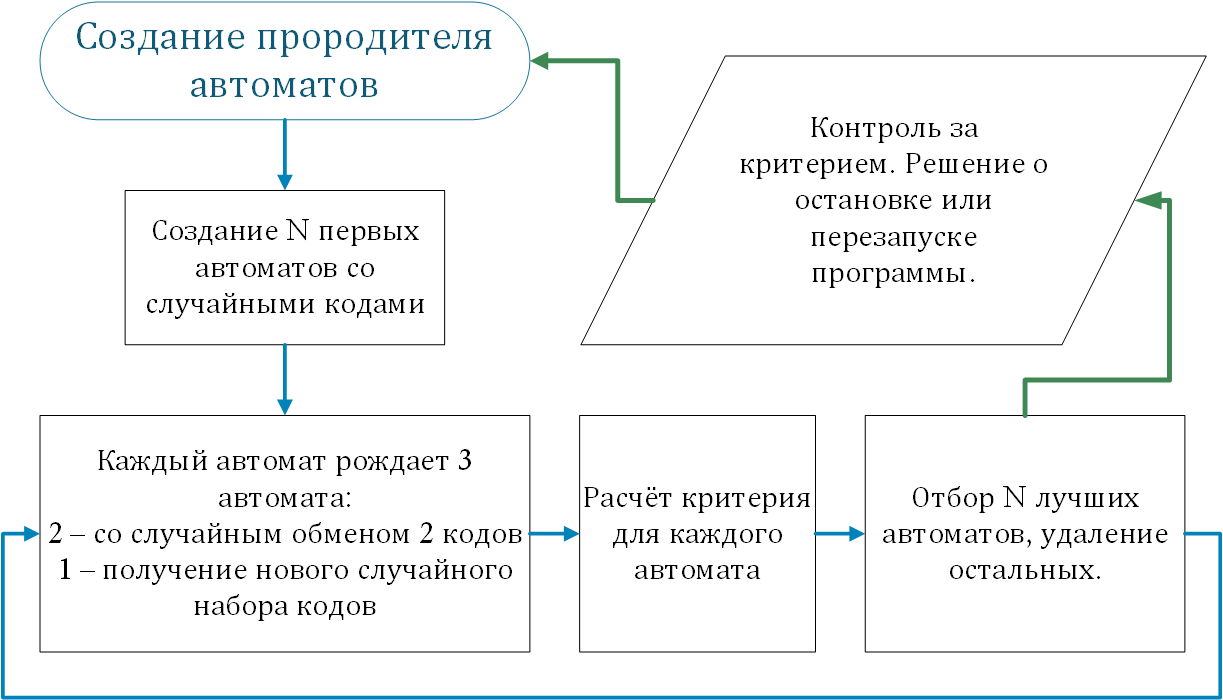
Результаты
Для исследования был спроектирован автомат с числом возможных вариантов задания состояний равным 6720. Для каждого варианта было рассчитано количество необходимых элементов для реализации.
Данный ЦА описывает поведение пчелы (для простоты восприятия), входной сигнал представляет 0(всё спокойно) или 1(пчела видит шершня).
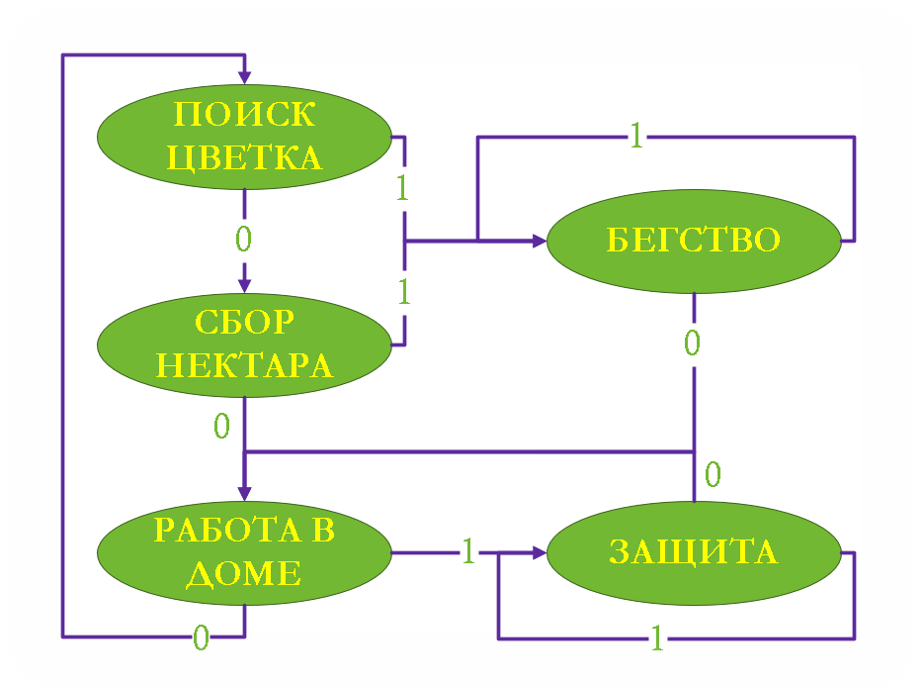
Описание ЦА:
Количество состояний: 5
Разрядность памяти: ceil(log2(5)) = 3
Разрядность входного сигнала: 1
Пример расчёта числа всех возможных вариантов построения автомата:
Для любой выборки(V) нашлось не менее X(X<S!) перестановок с наилучшим исходом. Наилучший исход -- исход с минимальным числом элементов необходимых для реализации данного автомата. Для поиска способа кодирования c наилучшим исходом достаточно перебрать S! вариантов.
Анализ показал, что наибольшая вероятность встретить автомат с наилучшим исходом -- если количество 0 и 1 в кодах состояний будет равнозначным.
Для сложных автоматов, где перебор занимает много времени, эффективным решением будет применить генетический алгоритм, он не обязательно найдёт наилучший исход, но позволит быстро найти решение близкое к нему.
