LinearLeopard 15 янв 2021 в 13:27

Constraint Programming или как решить задачу коммивояжёра, просто описав её

7 мин

12K

Python*Программирование*Искусственный интеллект

Туториал

Перевод

Пожалуй, наиболее популярной парадигмой программирования является императивное программирование. Но это не единственный вид программирования, широко известны функциональное и логическое программирование. Constraint Programming (Программирование в ограничениях/Ограниченное программирование) не так популярно. Но это очень мощный инструмент для решения комбинаторных задач. Вместо реализации алгоритма, который решает задачу, с последующей тратой кучи времени на его отладку, рефакторинг и оптимизацию, программирование с ограничениями позволяет вам просто описать модель в специальном синтаксисе, а особая программа (решатель - solver) найдет решение за вас (или скажет, если их нет). Впечатляет, не правда ли? Мне кажется, каждый программист должен знать о такой возможности.

Minizinc

Вероятно, наиболее часто используемым инструментом программирования ограничений (по крайней мере, в образовательных целях) является minizinc. Он предоставляет IDE для объявления моделей и несколько встроенных решателей для поиска ответа. Вы можете скачать программу с официального сайта.

Простая модель в Minizinc

Рассмотрим пример решения модели, начнем с криптоарифметической задачи. В данном типе задач все буквы следует заменить цифрами с двумя условиями:

равенство должно выполняться
одна и та же цифра не должна соответствовать разным буквам и наоборот.

Например, решим следующее уравнение:

    S E N D
+   M O R E
= M O N E Y

Структура модели

В minizinc каждая модель представляет собой набор переменных, параметров и ограничений. Переменные - это неизвестные значения, которые должен найти решатель, параметры - это некоторые константы, которые известны во время выполнения модели, вы можете изменять параметры от запуска к запуску, и, очевидно, это повлияет на результат.

Например, количество городов и расстояния между ними являются параметрами для задачи коммивояжёра, путь будет зависеть от них. Но программист может создать одну модель для задачи, а затем просто выполнить ее для разных параметров без изменения исходного кода модели.

Ограничения - это ограничения :), которым должны удовлетворять значения переменных.

Объявление модели

Приступим к собственно программированию. Здесь у нас есть 8 переменных (S, E, N, D, M, O, R, Y), они являются цифрами, поэтому они могут принимать значения от 0 до 9 (S и M от 1 до 9, потому что число не может начаться с нуля).

В синтаксисе minizinc это объявляется следующим образом:

var 1..9: S;
var 0..9: E;
var 0..9: N;
var 0..9: D;
var 1..9: M;
var 0..9: O;
var 0..9: R;
var 0..9: Y;

Далее следует указать равенство, в minizinc оно задается самым обычным образом:

constraint                1000 * S + 100 * E + 10 * N + D
                        + 1000 * M + 100 * O + 10 * R + E
           == 10000 * M + 1000 * O + 100 * N + 10 * E + Y;

Мы также должны указать, что каждая переменная имеет свои собственные значения и не должно быть переменных с одинаковым значением. Minizinc имеет специальное ограничение alldifferent, но оно не определено в стандартной библиотеке, необходимо подключить его специальной директивой include "alldifferent.mzn";.

И последнее, что необходимо сделать, это объявить, каким образом решать модель, есть 3 варианта: удовлетворить (satisfy), минимизировать (minimize) и максимизировать (maximize) какое-то значение, я думаю, их названия говорят сами за себя :).

Результирующий исходный код выглядит следующим образом:

include "alldifferent.mzn";

var 1..9: S;
var 0..9: E;
var 0..9: N;
var 0..9: D;
var 1..9: M;
var 0..9: O;
var 0..9: R;
var 0..9: Y;

constraint           1000 * S + 100 * E + 10 * N + D
                   + 1000 * M + 100 * O + 10 * R + E
       = 10000 * M + 1000 * O + 100 * N + 10 * E + Y;

constraint alldifferent([S,E,N,D,M,O,R,Y]);

solve satisfy;

output ["   ",show(S),show(E),show(N),show(D),"\n",
        "+  ",show(M),show(O),show(R),show(E),"\n",
        "= ",show(M),show(O),show(N),show(E),show(Y),"\n"];

Minizinc может выполнить модель и найти решение:

   9567
+  1085
= 10652

По умолчанию minizinc прекращает выполнение задачи satisfy после первого решения, это поведение можно изменить в настройках, вы можете повторно запустить эту модель и попросить minizinc найти все решения, но он скажет, что есть только одно :).

Заключение для первой части

Minizinc предоставляет мощный, общий и простой в использовании способ углубиться в constraint programming. Но он использует собственный синтаксис, который замедляет обучение и затрудняет интеграцию с другими языками программирования.

Интеграция с Python

minizinc-python решает вторую проблему, предоставляя способ вызова моделей minizinc из python, библиотека будет запускать minizinc, сериализовать ваш ввод и разбирать вывод, но программист по-прежнему должен писать довольно много строк кода. Мы можем посмотреть на пример решения квадратного уравнения:

Spoiler

У автора публикации сломался хабр и перестал выдавать список языков для подсветки синтаксиса в drop-down меню, если кто-то знает, как починить, буду очень признателен.

import minizinc

# Create a MiniZinc model
model = minizinc.Model()
model.add_string("""
var -100..100: x;
int: a; int: b; int: c;
constraint a*(x*x) + b*x = c;
solve satisfy;
""")

# Transform Model into a instance
gecode = minizinc.Solver.lookup("gecode")
inst = minizinc.Instance(gecode, model)
inst["a"] = 1
inst["b"] = 4
inst["c"] = 0

# Solve the instance
result = inst.solve(all_solutions=True)
for i in range(len(result)):
    print("x = {}".format(result[i, "x"]))

Лично для меня проблематично запомнить и воссоздать такой пример, а модель minizinc (которая представляет собой всего 4 строки кода) представлена в виде string, поэтому IDE и python не могут подсветить синтаксис и предоставить любую помощь и статические проверки для вас.

Zython

Почему бы не скрыть поиск решателя, создание экземпляров параметров, а также не предоставить способ реализации моделей на чистом Python?

Это то, что делает zython (miniZinc pYTHON). Это самый простой способ погрузиться в программирование с ограничениями*.

Spoiler

* из того, что я знаю

* по крайней мере, если вы разработчик на Python. :)

Чтобы начать работу с zython, у вас должны быть установлены python 3.6+ и minizinc в путь по умолчанию или доступен в $PATH. После этого можно скачать сам пакет и проверить установку

pip install zython
python
>>> import zython as zn

Если все было установлено правильно, вы не должны увидеть исключений и ошибок. После этого можно начинать изучить constraint programming с zython.

Send More Money

Сначала разберём уже известную модель — задачу "Send More Money"

import zython as zn


class MoneyModel(zn.Model):
    def __init__(self):
        self.S = zn.var(range(1, 10))
        self.E = zn.var(range(0, 10))
        self.N = zn.var(range(0, 10))
        self.D = zn.var(range(0, 10))
        self.M = zn.var(range(1, 10))
        self.O = zn.var(range(0, 10))
        self.R = zn.var(range(0, 10))
        self.Y = zn.var(range(0, 10))

        self.constraints = [(self.S * 1000 + self.E * 100 + self.N * 10 + self.D +
                             self.M * 1000 + self.O * 100 + self.R * 10 + self.E ==
                             self.M * 10000 + self.O * 1000 + self.N * 100 + self.E * 10 + self.Y),
                             zn.alldifferent((self.S, self.E, self.N, self.D, self.M, self.O, self.R, self.Y))]

model = MoneyModel()
result = model.solve_satisfy()
print(" ", result["S"], result["E"], result["N"], result["D"])
print(" ", result["M"], result["O"], result["R"], result["E"])
print(result["M"], result["O"], result["N"], result["E"], result["Y"])

Она должен вернуть тот же результат, что и раньше.

Однако кажется, всё еще довольно много кода. Но если мы посмотрим внимательнее, мы увидим, что это в основном объявление переменных и арифметическое уравнение, zython выполняет всю грязную работу, например, поиск решателя, создания экземпляра, его параметризацию, запуск модели и передачу решения в скрипт на python. Все, что вы делаете, это само программирование. Кроме того, zython предоставляет синтаксис Python для определения модели, что позволяет IDE выделять ваш код и проверять его на наличие ошибок перед запуском. Zython же дополнительно осуществляет проверки во время выполнения.

Генерация судоку

Создадим поле для судоку. Для этого необходимо использовать zn.Array. Массив может быть как переменной, так и параметром. Так как на момент запуска значения в ячейках поля судоку неизвестны и должны быть найдены в данном случае создаётся массив переменных.

import zython as zn


class MyModel(zn.Model):
    def __init__(self):
        self.a = zn.Array(zn.var(range(1, 10)), shape=(9, 9))

        self.constraints = \
            [zn.forall(range(9),
                       lambda i: zn.alldifferent(self.a[i])),
             zn.forall(range(9),
                       lambda i: zn.alldifferent(self.a[:, i])),
             zn.forall(range(3),
                       lambda i: zn.forall(range(3),
                                           lambda j: zn.alldifferent(self.a[i * 3: i * 3 + 3, j * 3: j * 3 + 3]))),
            ]


model = MyModel()
result = model.solve_satisfy()
print(result["a"])

Решение, выданное моделью будет зависить от версии minizinc, мне выдало следующее:

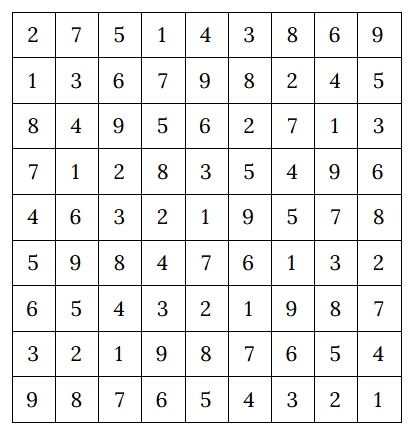
Задача коммивояжёра

Поскольку я обещал, что мы рассмотрим задачу коммивояжёра, давайте перейдём к ней. Данную модуль можно описать следующим образом:

import zython as zn


class TSP(zn.Model):
    def __init__(self, distances):
        self.distances = zn.Array(distances)
        self.path = zn.Array(zn.var(range(len(distances))),
                             shape=len(distances))
        self.cost = (self._cost(distances))
        self.constraints = [zn.circuit(self.path)]

    def _cost(self, distances):
        return (zn.sum(range(1, len(distances)),
                       lambda i: self.distances[self.path[i - 1],
                                                self.path[i]]) +
                self.distances[self.path[len(distances) - 1],
                               self.path[0]])


distances = [[0, 6, 4, 5, 8],
             [6, 0, 4, 7, 6],
             [4, 4, 0, 3, 4],
             [5, 7, 3, 0, 5],
             [8, 6, 4, 5, 0]]
model = TSP(distances)
result = model.solve_minimize(model.cost)
print(result)

Мы снова использовали массив в модели, но теперь это параметр, то есть его значения, определенны до выполнения модели.

Заключение для второй части

Constraint programming - концепция, достойная изучения, она может сэкономить время при решении множества проблем: составить расписание, определить, каких юнитов следует нанять, чтобы обладать самой сильной армией при заданном ограничении ресурсов в вашей любимой стратегии или помочь определить самую сильная сборку в вашей любимой ролевой игре, какие цвета вы должны использовать, чтобы покрасить географические регионы на карте таким образом, чтобы все соседствующие области имели разные цвета, и даже определить оптимальные интервалы в движении общественного транспорта и, какие тортики должна печь ваша пекарня для максимизации прибыли.

Zython предоставляет способ выразить модель constraint programming на чистом питоне и легко решить эту проблему. Вы можете увидеть больше примеров в документации.

Конструктивная критика, выражение своего мнения в комментариях, баг репорты, feature request'ы и PR одобряются.

Удачи в изучении программирования с ограничениями.

Теги:

Хабы: