Сколько стоит расписание

Основные данные вычислительных экспериментов по реорганизации ярусно-параллельной формы  (ЯПФ) информационных графов алгоритмов (ИГА) приведены в предыдущей публикации. Цель текущей публикации – показать окончательные результаты исследований разработки расписаний выполнения параллельных программ  в показателях вычислительной трудоёмкости собственно преобразования  и качества полученных расписаний. Данная работа является итогом вполне определённого цикла исследований в рассматриваемой области.

Как и было сказано ранее, вычислительную трудоёмкости (ВТ) в данном случае будем вычислять в единицах перемещения операторов с яруса на ярус в процессе реорганизации ЯПФ. Этот подход близок классической методике определения ВТ операций упорядочивания (сортировки) числовых массивов, недостатком является неучёт трудоёмкости  процедур определения элементов для перестановки.

Т.к. в принятой модели ЯПФ  фактически определяет порядок выполнения операторов параллельной программы (операторы выполняются группами по ярусам поочерёдно), в целях сокращения будем иногда использовать саму аббревиатуру “ЯПФ” в качестве синонима понятия плана (расписания) выполнения параллельной программы. По понятным причинам исследования  проводились на данных относительно небольшого объёма в предположении сохранения корректности полученных результатов при обработке данных большего размера.  Описанные в данной публикации исследования имеют цель продемонстрировать возможности имеющегося инструментария при решении поставленных задач.  При желании возможно исследовать произвольный алгоритм, описав и отладив его в модуле Data-Flow с последующим импортом в формате информационного графа в модуль SPF@home для дальнейшей обработки.

Основной целью преобразований ЯПФ продолжаем считать получение максимальной плотности кода (фактически максимальная загрузка имеющихся в наличии отдельных вычислителей параллельной вычислительной системы). Кстати, именно с этими понятиями связано известное зло-ироничное  высказывание об излишнем количестве NOP-инструкций в “связках” сверхдлинного машинного слова в вычислителях VLIW-архитектуры (даже при наличии участков полностью последовательного кода лакуны в сверхдлинном слове формально должны быть заполнены некоей операцией-“пустышкой”). В наличии NOP-операторов во VLIW-связке нет ничего постыдного – в алгоритмах встречаются чисто последовательные участки. Плохо, когда VLIW-связка малозаполнена  реально изменяющими данные операторами  постоянно (одна из причин приостановки проекта Itanium)…

Как и ранее, будем ссылаться на разработанные эвристические методы (иногда сокращённо именуемые просто  эвристиками), реализованные на языке Lua и управляющие преобразованиями ЯПФ. Также не учитываем возможности одновременного выполнения команд нескольких процессов на параллельном поле вычислителей (хотя теоретически это может привести к повышению плотности кода).

В приводимых исследованиях не учитывалось ограничение на  реальный объём памяти для временного хранения данных между ярусами операторов (обычно регистров общего назначения), это ограничение может ухудшить полученное  решение (а использование оперативной памяти для декларируемой цели - снизить быстродействие). С другой стороны, моделирование даёт возможность оценить разумный размер регистрового файла.   

Полученные результаты предназначаются для улучшения качества  разработки расписаний выполнения параллельных программ  в распараллеливающих компиляторах будущих поколений. При этом внутренняя реализация данных конечно, совсем  не обязана предусматривать явного построения ЯПФ в виде двумерного массива, как для большей выпуклости показано на рис.2 в этой публикации и выдаётся программным модулем SPF@home (http://vbakanov.ru/spf@home/content/install_spf.exe). Она может быть любой удобной для компьютерной реализации – например, в наивном случае устанавливающей однозначное соответствие между формой ИГА в виде множества направленных дуг {k,l} (матрица смежности) и двоек номеров вершин i_k,j_k и i_l,j_l, где i,j – номера строк и столбцов в ЯПФ (процедуру преобразования ИГА в начальную ЯПФ провести всё равно придётся, ибо в данном случае именно она выявляет параллелизм в заданном ИГА алгоритме; только после этого можно начинать любые преобразования ЯПФ).

Учитывая давно известный факт о продвижении активной (там, где в данный период времени происходит энергичное выполнение машинных команд) области операторов вдоль фронта выполняемой программы, при нехватке памяти обработку можно проводить блоками последовательно от начала выполнения программы к её концу – при этом выходные вершины предыдущего блока являются входными для последующего.

В данном случае исследования проводились над программами, каждая из которых представляет собой один из часто встречающихся алгоритмов обработки данных. Автор отдаёт отчёт в том, что реально исполняемые программы обладают существенно большей сложностью структуры (включая множество алгоритмов, процедуры обработки прерываний и др.), но считает, что на этапе моделирования процессов трудно подобрать в качестве объекта исследований  более подходящий материал, чем  распространённые алгоритмы обработки данных. Практичность такого выбора подтверждается известным фактом -  обычно основная вычислительная трудоёмкость программ сосредоточена именно в отдельных  алгоритмах (знаменитое “правило  90/10”), поэтому рационально оптимизировать (в вышеуказанном смысле) именно эти блоки; для реализации такого подхода в библиотеках полезно определить специальные метки, несущие информацию о типе алгоритма и эффективных методах его оптимизации.

Для каждой из группы рассматриваемых задач (преобразования с сохранением высоты исходной ЯПФ или при возможности увеличения высоты оной) рассмотрим по две методики (эвристики, ибо так согласились именовать разработки) – для первого  случая это “1-01_bulldozer” vs “1-02_bulldozer”, для второго - “WidthByWidtn” vs “Dichotomy”. Мне стыдно повторять это, но высота ЯПФ определяет время выполнения программы…

1. Получение расписания параллельного выполнения программ при сохранении высоты ЯПФ

Сохранение высоты исходной  ЯПФ равносильно выполнению алгоритма (программы) за минимально возможное время. Наиболее равномерная нагрузка на все вычислители параллельной системы будет при одинаковой ширине всех ярусов ЯПФ (среднеарифметическое значение). В ЯПФ реальных алгоритмов и размерности обрабатываемых данных среднеарифметическое значение является довольно большим (практически всегда много большим числа отдельных вычислителей в параллельной системе). Т.о. рассматриваемый случай не часто встречается в практике, но всё же должен быть разобран.

Для сравнения выберем часто анализируемые ранее алгоритмы и два эвристических метода целенаправленного преобразования их ЯПФ – эвристики “1-01_bulldozer” и “1-02_bulldozer”.

Результаты применения этих эвристик приведены на рис. 1-3; обозначения на этих рисунках (по осям абсцисс отложены показатели размерности обрабатываемых данных):

• графики a), b) и с) – ширина ЯПФ, коэффициент вариации (CV ширин ярусов ЯПФ),  число перемещений (характеристика вычислительной трудоёмкости) операторов соответственно;

• сплошные (красная), пунктирные (синяя) и штрих-пунктирные (зелёная) линии – исходные данные, результат применения эвристик “1-01_bulldozer” и  “1-02_bulldozer” cоответственно.

Рисунок 1. Параметры плана параллельного выполнения при сохранении высоты ЯПФ для алгоритма умножения квадратных матриц 2,3,5,7,10-го порядков (соответствует нумерации по осям абсцисс) классическим методом

Рисунок 2. Параметры плана параллельного выполнения при сохранении высоты ЯПФ для алгоритма вычисления коэффициента парной корреляции по 5,10,15,20-ти точкам (соответствует нумерации по осям абсцисс)

Рисунок 3. Параметры плана параллельного выполнения при сохранении высоты ЯПФ для алгоритма решения системы линейных алгебраических уравнений (СЛАУ) для 2,3,4,5,7,10-того порядка (соответствует нумерации по осям абсцисс) прямым (неитерационным) методом Гаусса

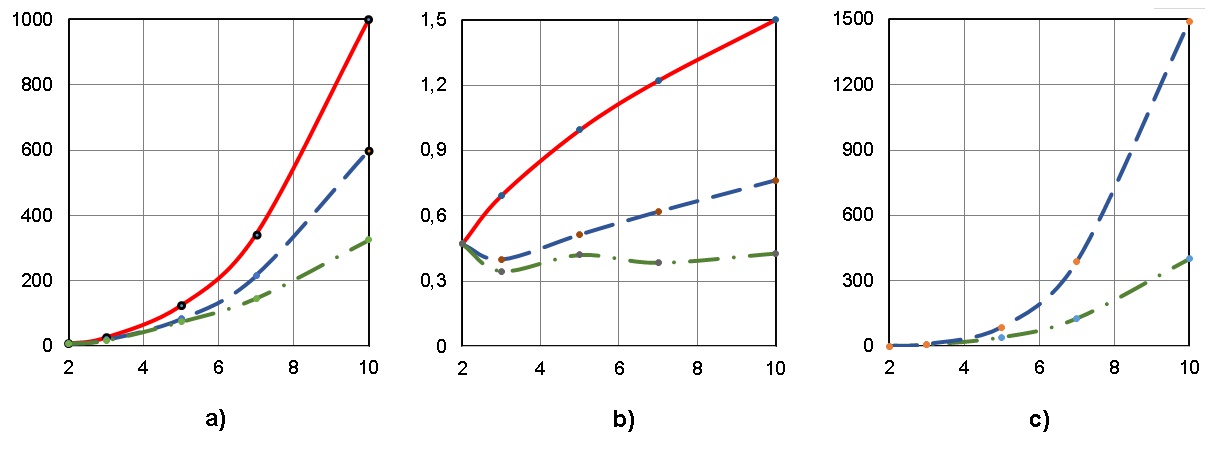
Данные рис. 1-3 показывают, что во многих случаях удаётся приблизиться к указанной цели. Напр., рис. 1a) иллюстрирует снижение ширины ЯПФ до 1,7 раз (метод “1-01_bulldozer”) и до 3 раз (метод “1-02_bulldozer”) при умножении матриц 10-го порядка.

Коэффициент вариации ширин ярусов ЯПФ (рис. 1b) приближается к 0,3 (граница однородности набора данных) при использовании эмпирики “1-02_bulldozer” и, что немаловажно, достаточно стабилен на всём диапазоне размерности данных.

Трудоёмкость достижения результата (рис. 1c) при использовании метода “1-02_bulldozer” значительно ниже (до 3,7 раз при порядке матриц 10) метода “1-01_bulldozer”.

Важно, что эффективность метода возрастает с ростом размерности обрабатываемых данных.

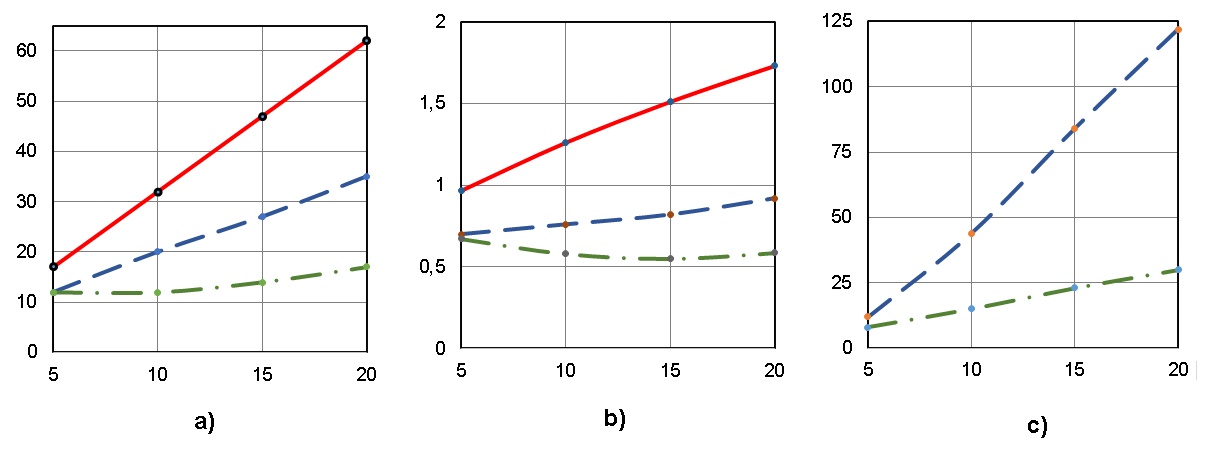
Не менее эффективным показал себя метод  “1-02_bulldozer” на алгоритме вычисления коэффициента парной корреляции (рис. 2).

Попытка реорганизации ЯПФ алгоритма решения системы линейных алгебраических уравнений (СЛАУ) порядка до 10 обоими методами (рис. 3) оказалась малополезной. Ширину ЯПФ снизить не удалось вообще (рис. 3a), снижение CV очень мало (рис. 3b), однако метод “1-02_bulldozer” немного выигрывает в трудоёмкости (рис. 3c).

Для большей полноты выводов объём исследований должен быть  расширен, однако уже сейчас ясно, далеко не каждый метод реорганизации ЯПФ одинаково эффективен для преобразования (в смысле построения рационального  расписания параллельного выполнения) различных алгоритмов. Т.к. принятый в данной работе общий подход предполагает итеративное приближение к наилучшему решению поставленной задачи, надлежит продолжить разработку новых эвристик (с учётом достигнутого).

2. Получение расписания параллельного выполнения программ на фиксированном числе параллельных вычислителей

Эта постановка задачи максимально близка к реальному случаю составления расписания для VLIW-машины с заданным числом процессорных команд в машинном слове (размер “связки”, “бандла” сверхдлинного машинного слова). При этом достигается и повышение плотности кода.

Ниже рассматривается распространенный случай выполнения программы на заданном гомогенном поле из  W параллельных вычислителей (от W=W₀ до W=1, где W₀ – ширина ЯПФ, а нижняя граница соответствует полностью последовательному выполнению). Сравниваем два метода реорганизации ЯПФ – “Dichotomy” и “WidthByWidtn”:

• “Dichotomy”. Цель – получить вариант ЯПФ с c шириной не более заданного W c увеличением высоты   методом перенесения операторов с яруса на вновь создаваемый ярус ниже данного. Если ширина яруса выше W, ровно половина операторов с него переносится на вновь создаваемый снизу ярус и так далее, пока ширина  станет не выше заданной W. Метод работает очень быстро, но “грубо” (высота ЯПФ получается явно излишней и неравномерность ширин ярусов высока).

• “WidthByWidtn”. Подлежат переносу только операторы яруса с числом операторов выше заданного N>W путём создания под таким  ярусом число ярусов М, равное:

Особенностью этой  эвристики является правило выбора конкретных операторов,  подлежащих переносу на вновь создаваемые ярусы.

На рис. 4,5  показаны результаты выполнения указанных эвристик в применении к двум распространенным алгоритмам линейной алгебры - умножение квадратных  матриц классическим методом  и решение системы линейных алгебраических уравнений прямым (неитерационным) методом Гаусса; красные и синие линии на этих и последующих рисунках соответствуют эвристикам “WidthByWidtn” и “Dichotomy” соответственно. Не забываем, что ширина реформированной ЯПФ  здесь соответствует числу команд в “связке” сверхдлинного машинного слова.

Рисунок 4. Возрастание высоты (ординаты) при ограничении ширины ЯПФ (абсциссы), разы; алгоритм умножения квадратных матриц классическим методом 5 и 10-го порядков – рис. a) и b) соответственно

Рисунок 5. Возрастание высоты (ординаты) при ограничении ширины ЯПФ (абсциссы), разы; алгоритм решения системы линейных алгебраических уравнений прямым (неитерационным) методом Гаусса 5 и 10-го порядков – рис. a) и b) соответственно

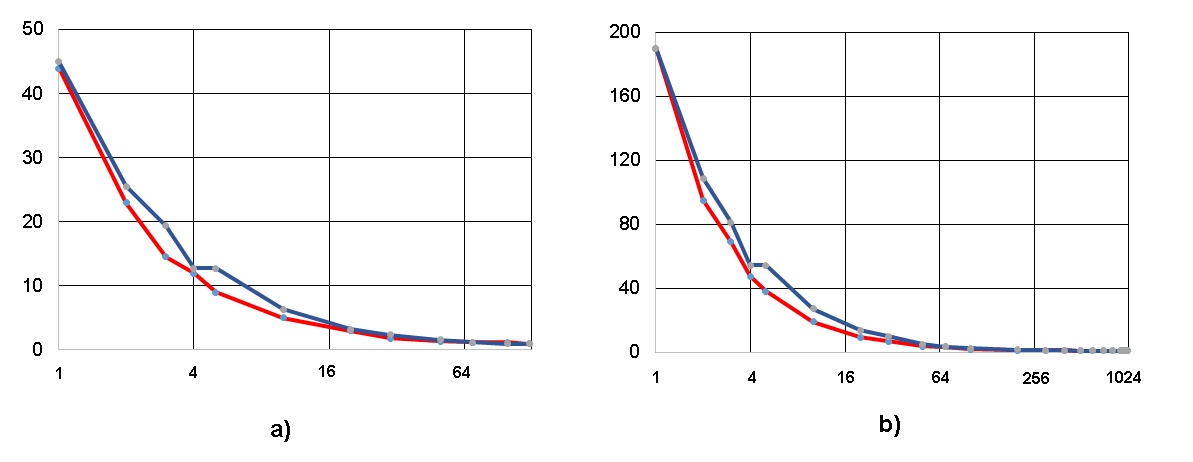
Как видно из рис. 4 и 5, оба метода на указанных алгоритмах приводят к близким результатам (из соображений представления ЯПФ плоской таблицей и инвариантности общего числа операторов в алгоритме это, конечно,  гипербола!). При большей высоте ЯПФ увеличивается время жизни данных, но само их количество в каждый момент времени снижается.

Однако “при всех равно-входящих” соответствующие методу “WidthByWidtn” кривые расположены ниже, нежели по методу “Dichotomy”; это соответствует несколько большему быстродействию. Полученные методом “WidthByWidtn” результаты практически совпадают с идеалом высоты ЯПФ, равным N_сумм./W_средн. , где N_сумм. – общее число операторов, W_средн. – среднеарифметическое числа операторов по ярусам ЯПФ при заданной ширине ея.

Рисунок 6. Число перемещений операторов между ярусами - a) и коэффициент вариации CV - b) при снижении ширины ЯПФ для алгоритма умножения квадратных матриц 10-го порядка классическим методом (ось абсцисс – ширина ЯПФ после реформирования)

Рисунок 7. Число перемещений операторов между ярусами - a) и коэффициент вариации CV - b) при снижении ширины ЯПФ для алгоритма решения системы линейных алгебраических уравнений 10-го порядка прямым (неитерационным) методом Гаусса (ось абсцисс – ширина ЯПФ после реформирования)

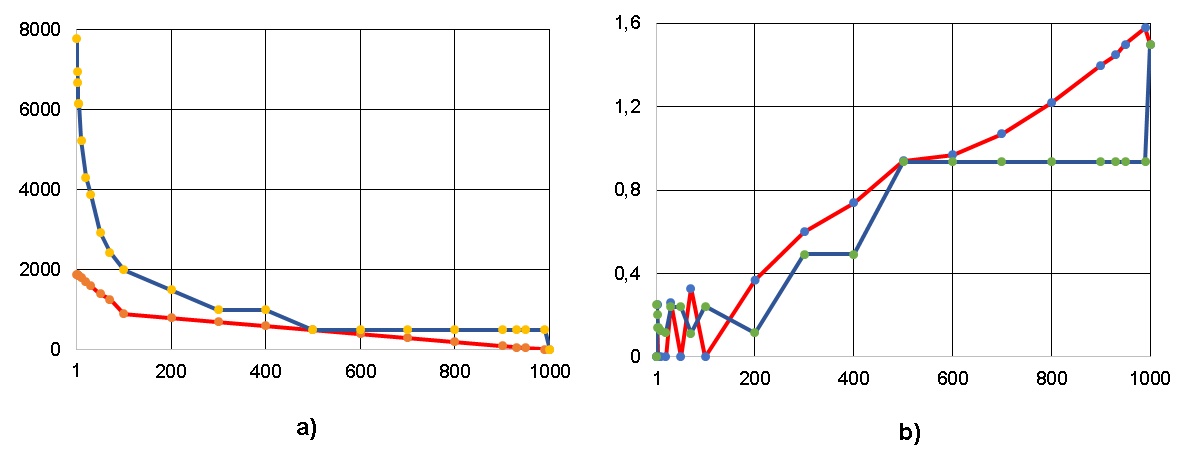
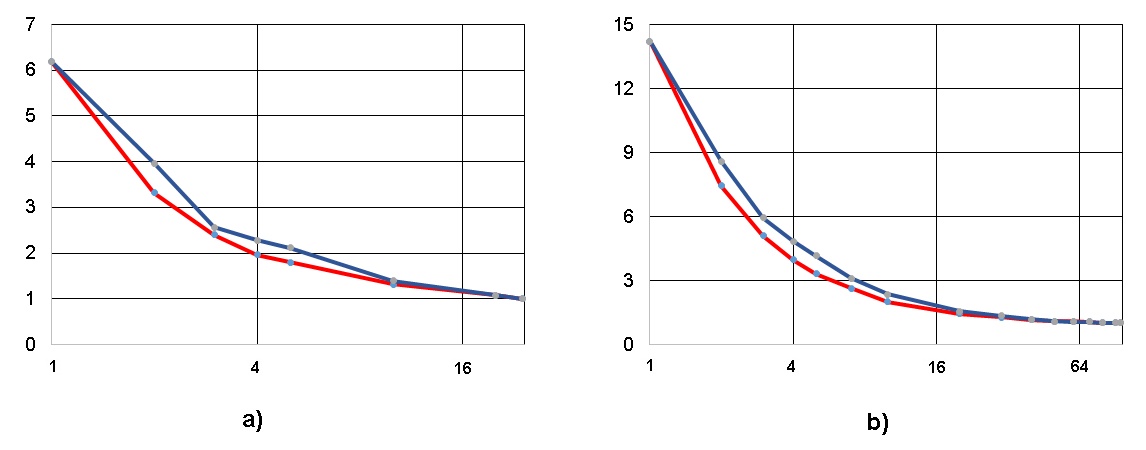
Анализ результатов, приведённый на рис. 6 и 7, более интересен (хотя бы потому, что имеет чисто практический интерес – вычислительную трудоёмкость преобразования ЯПФ). Как видно  из рис. 6 и 7, для рассмотренных случаев метод  “WidthByWidtn” имеет меньшую (приблизительно в 3-4 раза) вычислительную трудоёмкость (в единицах числа перестановок операторов с яруса на ярус) относительно метода “Dichotomy” (хотя на первый взгляд ожидается обратное). Правда, при этом метод (эвристика) “WidthByWidtn” обладает более сложной внутренней логикой по сравнению с “Dichotomy” (в последнем случае она примитивна). Логично использовать в распараллеливающих компиляторах  метод “Dichotomy” для быстрого (но достаточно “грубого”) построения планов выполнения параллельных программ, а метод “WidthByWidtn” – для построения этих планов в режиме  оптимизации.

Итак, в результате моделирования процесса обработки данных на параллельном вычислителе мы получили важные для организации синхронных вычислений практические данные (показатели близки полученным в публикации https://habr.com/ru/post/540122/, частичные отличия связаны с синхронностью вычислений):

1  Число параллельно работающих вычислителей (АИУ), необходимое для реализации максимально быстрого вычисления по заданному алгоритму (режим “неограниченного параллелизма”).

2  Зависимость времени вычислений от заданного количества параллельных вычислителей (вплоть до режима последовательного выполнения программы).

В результате моделирования дополнительно получены важные для организации вычислений практические данные, позволяющие априори выявить эффективные методы реорганизации (преобразования) последовательностей выполнения (планов, расписаний)  конкретных алгоритмов с целью их параллельной реализации на заданном поле параллельных вычислителей. Для практики особенно важно, что выбор методов преобразования произведён по естественными и понятным критериям - вычислительной трудоёмкости преобразований (от чего зависит время обработки) и неравномерности загрузки вычислительной системы (фактически коэффициента использования оборудования).

Собственно работы в области преобразования кода из одного вида в другой (Code Morphing) известны (см. здесь и здесь, в СМИ имеются данные об практике такой технологии применительно к отечественному VLIW-процессору ЭЛЬБРУС). Однако нет данных о серьёзных научно-методических  исследованиях в этом направлении - работы ведутся на основе или интуитивного подхода  или,  в лучшем случае, подхода, основанного на субъективном личностном опыте. Сказанное “доказу́ется” отсутствием (автор публикации специально искал информацию по данному вопросу) каких-либо объективных оценок вычислительной трудоёмкости используемых методов класса  Code Morphing. Т.к. данный блок CMS (Code Morphing Software)    будет использоваться при трансляции очень интенсивно, каждый процент повышения быстродействия имеет ценность.

Исходя из это, крайне практически полезны серьёзные методические разработки в области определения эффективных методов Code Morphing уровня машинных команд, позволяющие (в конечном результате) количественно оценивать (а значит – сравнивать и выбирать лучшие) различные методы. По мнению автора  наилучший методологический подход для этого  – математическое (с последующей компьютерной реализацией) моделирование.

Используя разработанное программное обеспечение, возможно анализировать любые алгоритмы по указанным критериям с целью выбора наиболее эффективных (минимально простых и максимально результативных) методов определения рациональных расписаний выполнения параллельных программ.

В соответствие  с присущим эвристическому подходу итерационному принципу постепенного приближения к наилучшему решению рассматриваемой задачи автор уверен в возможности количественного улучшения (относительно вышеприведённым параметрам) методик определения расписаний выполнения программ на заданном поле параллельных вычислителей.

На применя́емость в практике полученных моделированием результатов влияет выбор алгоритмов для моделирования и разме́рность обрабатываемых данных.  Конечно, в реальности будут выполняться последовательности действий (алгоритмы) иные, чем при (проведённом) моделировании. Однако при моделировании всегда приходится ограничивать диапазон исследуемых параметров, распространяя полученные результаты на  их бо́льшее число; а реальных (часто используемых в вычислительных практиках) алгоритмов, несомненно, повышает адекватность моделирования.

Данные экспериментов показывают, что увеличение размеров обрабатываемых данных приводит к повышения вариати́вности ЯПФ (под вариативностью будем понимать потенциал возможного перемещения операторов с яруса на ярус ЯПФ).

Формально показатель вариативности вычислялся в виде  величин V_n, V_t и V_nt. Здесь  V_n учитывает вклад числа операторов со свойством вариативности (вариабельности)  без учёта количественного значения самой этой величины, V_t - величину собственно вариабельности (V_n и V_t  обнуляются при отсутствии вариабельности и монотонно возрастают с её увеличением); V_nt - суперпозиция обоих предыдущих параметров в форме их произведения:  

V_n=N_v / N ,

V_t=⅀(T_i^max-T_i^min) / (T-1), причём суммирование ведётся по i - всем операторам  в ЯПФ,

V_nt=V_n х V_t ,

где N_v - число обладающих свойством вариативности (отличной от 0 возможностью перемещения между ярусами) операторов, N - общее число операторов, T - общее число ярусов, Ti^max и Ti^min  - максимальный и минимальный номера ярусов данной ЯПФ, на которых может располагаться i-тый оператор (фактически  диапазон возможного их расположения в единицах ярусов); данные приведены на рис. 8. 

Рисунок 8. Значения вариативности Vn – a), Vt – b) и Vnt – с) для алгоритмов умножения квадратных матриц классическим методом (красные кривые), умножения матрицы на вектор (синие), решения систем линейных алгебраических уравнений прямым неитерационным) методом Гаусса (зелёные кривые), вычисления коэффициентов прямой при аппроксимации точек методом наименьших квадратов (фиолетовые), вычисление коэффициентов параболы при аппроксимации точек методом наименьших квадратов (серые) и вычисление коэффициентов парной корреляции (оранжевые) в зависимости от размера исходных данных (порядка матриц в первых двух случаях и числа аппроксимируемых точек в последнем)

По данным рис. 8 наиболее полно отражающим ситуацию с изменением вариативности следует признать, пожалуй, параметр Vt (рис. 8 b).

Считая предложенные коэффициенты вариативности адекватно определяющими потенциал преобразования ЯПФ, надлежит сделать вывод об увеличении возможностей целенаправленного реформирования ЯПФ при возрастании размерности обрабатываемых данных.

Разработанные методики являются необходимым шагом к реализации распараллеливающих блоков трансляторов  для заданной архитектуры и системы команд процессора. При этом для архитектуры VLIW под термином “оператор” следует понимать именно машинную команду (здесь имеем полное сле́дование концепции ILP – Instruction-Level Parallelism, Параллелизм на Уровне Команд). Для многопоточных систем на многоядерных процессорах “оператор” логично соотнести  с гранулой параллелизма значительно бо́льшего размера (напр., уровня оператора/операторов или процедур языка программирования высокого уровня), последний вариант хорошо укладывается в концепцию  интерпретаторов. В обоих случаях представленная общая методика  построения рационального плана выполнения параллельной программы остаётся неизменной.

На практике придётся учесть немало практических вопросов реализации (включая известные проблемы использования указателей, конфликтов операций работы с памятью в связках Load/Store - https://habr.com/ru/post/575302/, http://ftp.altlinux.org/pub/people/mike/elbrus/docs/elbrus_prog/html/chapter6.html#id14 etc), однако при отсутствии общего подхода к решению проблемы конкретное исполнение практически всегда оказывается малоэффективным.

---

Предыдущие публикации на тему исследования параметров функционирования вычислительных систем методами математического моделирования:

• Есть ли параллелизм в произвольном алгоритме и как его использовать лучшим образом (https://habr.com/ru/post/530078/, 26.11.2020)

• Такие важные  короткоживущие данные (https://habr.com/ru/post/534722/, 24.12.2020)

• Это непростое условное выполнение (https://habr.com/ru/post/535926/, 03.01.2021)

• Динамика потокового вычислителя  (https://habr.com/ru/post/540122/, 01.02.2021)

• Параллелизм и плотность кода (https://habr.com/ru/post/545498/,   05.03.2021)

• Сколько стоит расписание (https://habr.com/ru/post/551688/, 10.04.2021) - текущая

• Параллелизм в алгоритмах - выявле́ние и рациональное его использование. Возможности компьютерного моделирования (https://habr.com/ru/articles/688196/, 14.09.2022)

• Построение планов параллельного выполнения программ для процессоров со сверхдлинным машинным словом (проект) (https://habr.com/ru/articles/792744/, 10.02.2024)