SergeyBPshenichnikov 10 апр 2021 в 21:51

Как преобразовать текст в алгебру: примеры

5 мин

4.3K

Поисковые технологии*Семантика*Алгоритмы*Natural Language Processing*

В предыдущей статье было разработано представление знаковых последовательностей полиномами матричных единиц на примере языкового текста. Текст превращается в алгебраический объект. С текстом можно совершать все алгебраические операции, необходимые для структуризации -- вычисления заголовков, словарей, аннотаций, смысловой разметки. В данной статье приведены два примера алгебраической структуризации текстов иной природы. Азбука Морзе выбрана из-за предельной краткости словаря, а математические формулы как пример обратной задачи.

1. Код Морзе-Вейля-Герке как алгебра матричных единиц

В азбуке Морзе знаковые последовательности (тексты) 26 латинских букв состоят из точек и тире. Пример выбран из-за предельной краткости словаря ("точка" и "тире").

Слова здесь - точки или тире. 26 букв азбуки - тексты из таких слов. У каждого слова две координаты. Первая координата – номер слова (точки или тире) в этой букве (от одного до четырех). Вторая координата – номер в словаре (1 или 2). Словарь E₁₁ ("точка") и E₂₂ ("тире").

$D_R=E_{11}+E_{22}$

Таблица 1. Азбука Морзе: латинские буквы как знаковые последовательности (тексты)

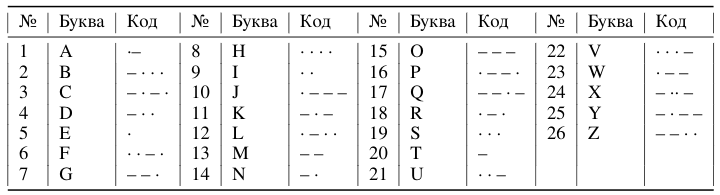
Каждой букве (знаковой последовательности) с номером из Таблицы 1 можно поставить в соответствие матричный полином P из матричных единиц 4x4 по формуле (8) из статьи [1].

Таблица 2: Азбука Морзе: буквы как матричные полиномы

Например, букве Q (№17) ставится в соответствие матричный полином:

$E_{12}+E_{22}+E_{31}+E_{42}= \begin{Vmatrix} 0 & 1 & 0 & 0\\ 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \end{Vmatrix}.$

Свойством всех 26 полиномов-букв таблицы 2 является то, что крайними правыми сомножителями являются только три матричные единицы E₁₂, E_21, E₃₂

Если все 26 полиномов Таблицы 2 представить столбцом ||P||, а также из того, что для матриц и столбцов выполняется:

$\begin{Vmatrix} a_{11} & \ldots & a_{1n}\\ \ldots & \ldots & \ldots\\ a_{m1} & \ldots & a_{mn} \end{Vmatrix} \begin{Vmatrix} b_{1} \\ \ldots \\ b_{n} \end{Vmatrix}= \begin{Vmatrix} a_{11} \\ \ldots \\ a_{m1} \end{Vmatrix}b_1+\ldots + \begin{Vmatrix} a_{1n} \\ \ldots \\ a_{mn} \end{Vmatrix}b_n,$

то азбука Морзе структурируется в три левые идеалы наборов матричных полиномов Таблицы 2 с базисами ||P||₁, ||P||₂, ||P||₃.

где

$\left\|P\right\|_1=\begin{Vmatrix} E_{12} \\ E_{21} \\ E_{32} \end{Vmatrix}, \left\|P\right\|_2=\begin{Vmatrix} E_{12} \\ E_{21}E_{12} \\ E_{12}+E_{21}E_{12} \\ E_{12}E_{21} \\ E_{21} \\ E_{21}+E_{12}E_{21} \\ E_{32} E_{21} + E_{43}E_{32} E_{21} \\ E_{43}E_{32} E_{21} \\ E_{32} E_{21} \\ E_{32} \\ E_{32} + E_{43}E_{32} \\ E_{43}E_{32} \end{Vmatrix}, \left\|P\right\|_3=\begin{Vmatrix} E_{12}E_{21} \\ E_{12} \\ E_{21} \\ E_{21}E_{12} \\ E_{32}E_{21} \\ E_{32} \\ E_{43}E_{32} E_{21} \\ E_{43}E_{32} \end{Vmatrix}, (1.1)$

||P||₂(||P||₂)^T - симметричная матрица - число в диагональных элементах – это число базисных элементов (простых и составных матричных единиц), принадлежащих букве, в других элементах – число совпадающих базисных элементов в соответствующей паре знаковых последовательностей (букв) - после нормализации характеризует важность буквы в азбуке.

(||P||₂)^T||P||₂ - симметричная матрица - число в диагональных элементах – это число букв, принадлежащих базисным элементам, в недиагональных элементах – число совпадающих букв в соответствующей паре базисных элементов – после нормализации характеризует важность базисного элемента (заголовка) в азбуке.

Азбука Морзе алгебраически структурирована в три идеала (класса) с базисами (1.1). Представление азбуки через идеалы описывает все подобные коды с базисами (1.1). Представление азбуки через идеалы приведено в Таблицах 3 и 4:

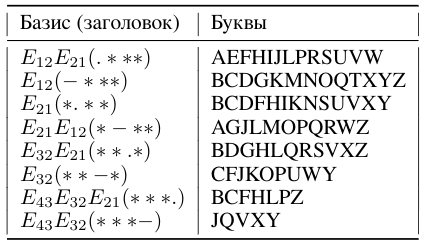
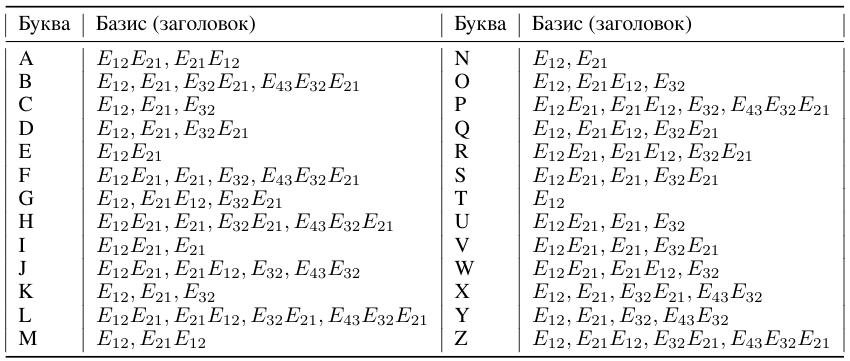
Азбука Морзе: ABCDEFGHIJKLMNOPQRSTUVWXYZ

из-за свойств матричных полиномов(крайние правые сомножители - только три матричные единицы E₁₂, E_21, E₃₂) разбивается на три класса (три идеала) тремя образующими E₁₂, E_21, E₃₂:

E₁₂ - заголовок тех букв, которые имеют знак «тире» на первом месте 4-знаковой последовательности:

_BCD__G___K_MNO_Q__T___XYZ (13 букв)

E₂₁ - заголовок тех букв, которые имеют знак «точка» на втором месте 4-знаковой последовательности:

_BCD_F_HI_K__N____S_UV_XY_ (13 букв)

E₃₂ - заголовок тех букв, которые имеют знак «тире» на третьем месте 4-знаковой последовательности:

__C__F___JK ___OP____U_W_Y_ (9букв)

2. Алгебра математического текста

В примере [1] языковый текст превращался в математический объект (матричный полином), с которым можно совершать алгебраические операции для анализа и синтеза текстов. В этом примере совершается обратное преобразование – математические объекты (формулы) сначала рассматриваются как тексты (знаковые последовательности), которые затем превращаются опять в математические объекты, но иные, чем исходные. Такая новая форма позволяет более системно находить свойства математических объектов для сравнения и классификации.

Формулы объема конуса V_K, цилиндра V_ц и тора V_Т:

$V_K=\frac{1}{3}\pi R_1^2H_1, V_{\text{Ц}}=\pi R_2^2H_2, V_T=\pi^2\left(R_3+R_4\right)r,\ \ \ \ \ \ \ \ \ (2.1)$

рассматриваются как тексты. Это означает, что входящие в тексты знаки не являются математическими объектами и для них отсутствуют алгебраические операции. Например, R₁² – это R₁R₁, πR₁ – это не произведение двух чисел, а просто последовательность двух знаков. Знаки в (1): R₁ и H₁ – радиус основания и высота конуса, R₂ и H₂ – радиус основания и высота цилиндра, R₃ – внутренний радиус тора, R₄ – внешний радиус тора, r – радиус образующей окружности тора, π – это число π.

Для семиотического анализа формул как текстов важно наличие повторов знаков. Повторы определяют закономерности. В формулах (2.1) повторов знаков на самом деле больше, чем указанные повторы знака π. Знаки R₁, R₂, R₃, R₄, H₁, H₂ и r – это длины отрезков. Тогда один из знаков, например , является простым (эталон длины), а остальные знаки – составными: R₁=ar, R₂=br, R₃=cr, R₄=dr, H₁=er, H₂=fr . Тогда правые части формул (2.1):

$\begin{gathered} \frac{1}{3}\pi ararer \\ \pi brbrfr \\ \pi \pi \left(c+d \right)rr \end{gathered} \ \ \ \ \ \ \ \ \ \ \ \ (2.2)$

Или в индексной форме:

$\begin{gathered} \left(\frac{1}{3}\right)_{1,1}(\pi)_{2,2}(a)_{3,3} (r)_{4,4} (a)_{5,3} (r)_{6,4} (e)_{7,7} (r)_{8,4} \\ (\pi)_{9,2} (b)_{10,10} (r)_{11,4} (b)_{12,10} (r)_{13,4} (f)_{14,14} (r)_{15,4} \\ (\pi)_{16,2} (\pi)_{17,2} \left(c+d \right)_{18,18} (r)_{19,4}(r)_{20,4} \end{gathered} \ \ \ \ \ \ \ \ \ (2.3)$

Формулы (2.2) как полином матричных единиц из трех фрагментов

$P=F_1(P)+F_2(P)+F_3(P), \ \ \ \ \ \ \ \ \ \ (2.4)$

где:

$\begin{gathered} F_1(P) = D_L\left(E_{1,1}+E_{2,2}+E_{3,3}+E_{4,4}+E_{5,3}+E_{6,4}+E_{7,7}+E_{8,4}\right)D_R \\ F_2(P) = D_L\left(E_{9,2}+E_{10,10}+E_{11,4}+E_{12,10}+E_{13,4}+E_{14,14}+E_{15,4}\right) D_R \\ F_3(P) = D_L\left(E_{16,2}+E_{17,2}+E_{18,18}+E_{19,4}+E_{20,4}\right) D_R \\ D_R = E_{1,1}+E_{2,2}+E_{3,3}+E_{4,4}+E_{7,7}+E_{10,10}+E_{14,14}+E_{18,18} \\ D_L = E_{1,1}+E_{2,2}+E_{3,3}+E_{4,4}+E_{5,5}+E_{6,6}+E_{7,7}+ \ldots + E_{20,20} = E \\ D_L=D_R+E_{5,5}+E_{6,6}+E_{5,5}+E_{8,8}+E_{5,5}+E_{9,9} \end{gathered}$

Или в блочно-матричной форме:

В столбцах P находятся знаки из трех формул (2.1) . Если в столбце два нуля, это означает, что соответствующий знак имеется только в одной формуле. Например, знак «1/3» (или E_1,1), два знака «a» (или E_3,3+E_5,3) , один знак «e» (или E_7,7) имеются только в первой формуле для конуса (первая строка (2.5)). Только в цилиндре (вторая строка (2.5)) имеются два знака «b» (или E_11,11+E_13,11) и один «f» (или E_15,15). Только в торе (третья строка (2.5)) имеется знак (c+d) (или E_20,20). Общие знаки конуса, цилиндра и тора находятся во втором и четвертом столбцах (2.5). Тогда:

$\begin{gathered} P = P_{\text{частн}_1}P_{\text{дел}_1}+P_{\text{ост}} \\ P = P_{\text{частн}_2}P_{\text{дел}_1}+P_{\text{ост}} \end{gathered}$

где:

$\begin{gathered} P_{\text{частн}_1} = \left(E_{2,18}+E_{4,12}+E_{6,14}+E_{8,16}\right) +\left(E_{10,18}+E_{12,12}+E_{14,4}+E_{16,16}\right)+\\ +\left(E_{18,18}+E_{19,19}+E_{21,12}+E_{22,14}\right), \\ P_{\text{частн}_2} = (E_{2,2}+E_{4,4}+E_{6,4}+E_{8,4})+(E_{10,2}+E_{12,4}+E_{14,4}+E_{16,4})+ \\ +(E_{18,2}+E_{19,2}+E_{21,4}+E_{22,4}), \\ P_{\text{дел}_1} = E_{18,2} + E_{19,2}+E_{12,4} + E_{14,4} + E_{16,4}, \\ P_{\text{дел}_2} = E_{2,2} + E_{4,4}, \\ P_{\text{ост}} = E_{1,1}+E_{3,3} + E_{5,3}+E_{7,7}+E_{11,11} + E_{13,11}+E_{15,15}+E_{20,20}.\\ \end{gathered}$

В (2.6) матричный текст раскладывается по разным базисам P_дел1 и P_дел2. Базис P_дел1 учитывает взаимные положения между повторяющимися знаками относительно тора в формулах (2.1). Базис P_дел2 учитывает положения между повторяющимися знаками относительно знаков словаря D_R в формулах (2.1). В общем случае учет положения знаков в формулах существенен, если знаки некоммутативны (например, знаки – это матрицы, вектора, тензоры, гиперкомплексные числа). Но и в скалярном это полезно, например, канонической является формула площади круга π r^₂, а не r^₂π.

Базис Гребнёра-Ширшова для (2.6):

$\begin{gathered} P_{\text{дел}_1}+P_{\text{ост}} \\ P_{\text{дел}_2}+P_{\text{ост}} \end{gathered}$

Тогда:

$\begin{gathered} P= P_{\text{частн}_1} \left( P_{\text{дел}_1}+P_{\text{ост}} \right) \\ P= P_{\text{частн}_2} \left( P_{\text{дел}_2}+P_{\text{ост}} \right) \end{gathered}$

В P_частн1 и P_частн2 имеются повторы (зацепления матричных единиц по второму индексу). Они подлежат дальнейшей редукции. Все зацепления разрешимы, - аддитивные P_частн1 и P_частн2 приобретут мультипликативную форму, как и для языкового примера.

Метод алгебраической структуризации текстов позволяет для текстов разной природы найти соответствующие классификаторы и словари. Т. е. классифицировать тексты без априорного задания признаков классификации и наименования классов. Такая классификация называется категоризацией или апостериорной классификацией. Например, для (2.3) классификационными признаками становятся:

P_дел1 и P_дел2 (общие π и r в разных местах формул),
общее число слагаемых в круглых скобках P_частн1 и P_частн2 (четыре),
соотношения числа π и r в круглых скобках P_частн1 и P_частн2(1,1,2 и 3,3,2),
сомножители мультипликативной формы P_частн1 и P_частн2,
всевозможные фрагменты P_ост (вычеты, как класс формул с остатком-фрагментом).

Наименования классов совпадают с наименованием признаков и их сочетаний.

Литература

[1] Пшеничников C.Б. Алгебра текста. Researchgate Preprint, 2021

Теги:

Хабы:

Как преобразовать текст в алгебру: примеры

1. Код Морзе-Вейля-Герке как алгебра матричных единиц

2. Алгебра математического текста

Литература

Публикации

Истории

Ближайшие события